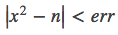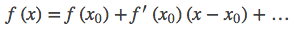求平方根的幾種方法
求解 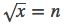
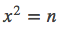
二分法
以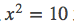
c++程式碼如下:
float dichotomyMethod(float n, float err)
{
float bigNum = n;
float smallNum = 0;
float midNum = 0;
float errTemp = 0;
do
{
if(errTemp > 0)
bigNum = midNum;
else
smallNum = midNum;
midNum = (bigNum + smallNum) / 2.0 牛頓迭代法
之前一直不知道這種方法,直到上了一門《數值分析》的課。當然是考試前複習的時候才直到的,O(╯□╰)O 。這種方法能夠花比較少的次數接近結果,在單根附近有平方收斂。
對於
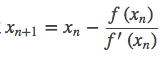
上面的式子很簡單,幾何上的意義是點Xn處的切線與x軸得到的交點就是 Xn+1。下面這張動圖能比較好說明。

代數上是對 f(x) 進行泰勒展開,並取前兩項。
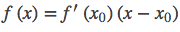 ,和之前提到的迭代表達式一致。
,和之前提到的迭代表達式一致。
c++程式碼如下:
float newtonIterationMethod(float n, float err)
{
float x = n;
float temp = x;
do
{
temp = x;
x = (x + n / x) / 2.0;
}while(fabs(x * x - n) > err);
return x;
}對比下以上兩種方法所花的時間。計算1000次總時間的對比:
- 二分法 625us
- 牛頓迭代法 193us
牛頓迭代法勝出,差距還是比較明顯。
神奇方法
在部落格上看到一種很神奇的方法,是來自遊戲Quake III的原始碼,求得是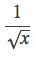
float InvSqrt (float x)
{
float xhalf = 0.5f*x;
int i = *(int*)&x;
i = 0x5f3759df - (i>>1);
float y = *(float*)&i;
y = y*(1.5f - xhalf*y*y);
return y;
}對於遊戲來說,速度比精度重要,不像科學計算那樣。這種方法做了一些近似,精度不一定高,但是速度快。可以看到,這方法僅僅用了一句i = 0x5f3759df - (i>>1);就完成了計算,後面加了牛頓迭代提高精度(想得到更高的精度可以多迭代幾次)。
具體原理可以看上面提高的部落格,反正我是沒看懂……站在數學制高點的人程式設計真的就是開掛啊,喂。
三種方法加自帶函式的時間對比(1000次,只是巨集觀上的對比,編譯器可能會有優化):
- 二分法 600us
- 牛頓迭代法 150us
- 神奇方法 26us
- 自帶sqrt 19us
有趣的是,據說提到的這種神奇的方法在10幾年前比自帶的sqrt函式快4倍左右,現在編譯器各種優化加硬體上的變化,也許也有演算法上的改變,使得自帶的sqrt函式變快了。一個sqrt都能玩的這麼溜,也是服了。
csdn部落格mardwon模式不能渲染Latex公式真的煩!