深度學習:神經網路中的啟用函式
軟飽和和硬飽和
優點:
在特徵相差比較複雜或是相差不是特別大時效果比較好(這樣飽不飽和就沒那麼在影響了?)。
sigmoid啟用函式在除了前饋網路以外的情景中更為常見。迴圈網路、許多概率模型以及一些自編碼器有一些額外的要求使得它們不能使用分段線性啟用函式,並且使得sigmoid單元更具有吸引力,儘管它存在飽和性的問題
缺點:
1 啟用函式計算量大,反向傳播求誤差梯度時,求導涉及除法;
2 與分段線性單元不同,sigmoid單元在其大部分定義域內都飽和——當z取絕對值很大的正值時,它們飽和到一個高值,當z取絕對值很大的負值時,它們飽和到一個低值,並且僅僅當z接近0時它們才對輸入強烈敏感。sigmoid單元的廣泛飽和性會使得基於梯度的學習變得非常困難。因為這個原因,現在不鼓勵將它們用作前饋網路中的隱藏單元。當使用一個合適的代價函式來抵消sigmoid的飽和性時,它們作為輸出單元可以與基於梯度的學習相相容。[深度學習]
sigmoid單元在反向傳播時,很容易就會出現梯度消失的情況,從而無法完成深層網路的訓練。Sigmoids saturate and kill gradients.
一般來說, sigmoid 網路在 5 層之內就會產生梯度消失現象。
梯度消失問題至今仍然存在,但被新的優化方法有效緩解了,例如DBN中的分層預訓練,Batch Normalization的逐層歸一化,Xavier和MSRA權重初始化等代表性技術。這個問題也可以通過選擇啟用函式進行改善,比如PReLU;在LSTM中你可以選擇關閉“遺忘閘門”來避免改變內容,即便打開了“遺忘閘門”,模型也會保持一個新舊值的加權平均。
3 Sigmoid 的 output 不是0均值。這是不可取的,因為這會導致後一層的神經元將得到上一層輸出的非0均值的訊號作為輸入。產生的一個結果就是:如果資料進入神經元的時候是正的(e.g. x>0 elementwise in f=wTx+b),那麼 w 計算出的梯度也會始終都是正的或者始終都是負的 then the gradient on the weights w will during backpropagation become either all be positive, or all negative (depending on the gradient of the whole expression f)。 當然了,如果你是按batch去訓練,那麼那個batch可能得到不同的訊號,所以這個問題還是可以緩解一下的。因此,非0均值這個問題雖然會產生一些不好的影響,不過跟上面提到的 kill gradients 問題相比還是要好很多的。
Tanh函式/雙曲正切函式

tanh 是sigmoid的變形:tanh(x)=2sigmoid(2x)−1
取值範圍為[-1,1]。
tanh評價
優點:
1 tanh在特徵相差明顯時的效果會很好,在迴圈過程中會不斷擴大特徵效果。
2 與 sigmoid 的區別是,tanh 是 0 均值的,因此實際應用中 tanh 會比 sigmoid 更好。文獻 [LeCun, Y., et al., Backpropagation applied to handwritten zip code recognition. Neural computation, 1989. 1(4): p. 541-551.] 中提到tanh 網路的收斂速度要比sigmoid快,因為 tanh 的輸出均值比 sigmoid 更接近 0,SGD會更接近 natural gradient[4](一種二次優化技術),從而降低所需的迭代次數。3 tanh更像是單位函式,更易訓練。

缺點:
也具有軟飽和性。
與sigmod曲線比較

硬雙曲正切函式(hard tanh)
它的形狀和 tanh 以及整流線性單元類似,但是不同於後者,它是有界的,g(a) = max(−1, min(1, a))。它由 Collobert (2004)引入。HTanh function
整流線性單元 ReLU
Rectified Linear Unit(ReLU) 整流線性單元通常作用於仿射變換之上:
當初始化仿射變換的引數時,可以將b的所有元素設定成一個小的正值,例如0.1。這使得整流線性單元很可能初始時就對訓練集中的大多數輸入呈現啟用狀態,並且允許導數通過。
f(x)=max(0,x)
輸入訊號 <0 時,輸出都是0,>0 的情況下,輸出等於輸入。
曲線
曲線如圖
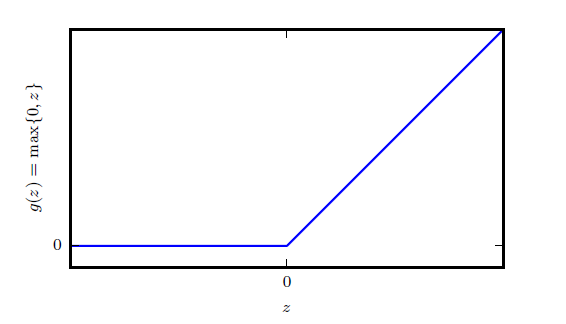

對比sigmoid類函式主要變化是:
1)單側抑制
2)相對寬闊的興奮邊界
3)稀疏啟用性。
ReLU 的導數(不存在sigmoid 的梯度消失的問題):

ReLU評價
ReLU 在x<0 時硬飽和。由於 x>0時導數為 1,所以,ReLU 能夠在x>0時保持梯度不衰減,從而緩解梯度消失問題。但隨著訓練的推進,部分輸入會落入硬飽和區,導致對應權重無法更新。這種現象被稱為“神經元死亡”。
ReLU 的優點:
- 速度快 和sigmoid函式需要計算指數和倒數相比,relu函式其實就是一個max(0,x),計算代價小很多。
- 減輕梯度消失問題 回憶一下計算梯度的公式。其中,是sigmoid函式的導數。在使用反向傳播演算法進行梯度計算時,每經過一層sigmoid神經元,梯度就要乘上一個。從下圖可以看出,函式最大值是1/4。因此,乘一個會導致梯度越來越小,這對於深層網路的訓練是個很大的問題。而relu函式的導數是1,不會導致梯度變小。當然,啟用函式僅僅是導致梯度減小的一個因素,但無論如何在這方面relu的表現強於sigmoid。使用relu啟用函式可以讓你訓練更深的網路。
- 稀疏性 通過對大腦的研究發現,大腦在工作的時候只有大約5%的神經元是啟用的,而採用sigmoid啟用函式的人工神經網路,其啟用率大約是50%。有論文聲稱人工神經網路在15%-30%的啟用率時是比較理想的。因為relu函式在輸入小於0時是完全不啟用的,因此可以獲得一個更低的啟用率。
或者優點等價的解釋為:
Krizhevsky et al. 發現使用 ReLU 得到的SGD的收斂速度會比 sigmoid/tanh 快很多(看右圖)。有人說這是因為它是linear,而且非飽和的 non-saturating。相比於 sigmoid/tanh,ReLU 只需要一個閾值就可以得到啟用值,而不用去算一大堆複雜的運算。
雖然2006年Hinton教授提出通過分層無監督預訓練解決深層網路訓練困難的問題,但是深度網路的直接監督式訓練的最終突破,最主要的原因是採用了新型啟用函式ReLU。與傳統的sigmoid啟用函式相比,ReLU能夠有效緩解梯度消失問題,從而直接以監督的方式訓練深度神經網路,無需依賴無監督的逐層預訓練。
ReLU 的缺點:
當然 ReLU 也有缺點,就是訓練的時候很”脆弱”,很容易就”die”了。舉個例子:一個非常大的梯度流過一個 ReLU 神經元,更新過引數之後(lz:引數很可能變為一個很大的負值,之後正向傳播時很大概率會使啟用aj為0,就死了δj = σ'(aj)∑δkwkj中aj為0之後δj也一直為0),這個神經元可能再也不會對任何資料有啟用現象了。如果這個情況發生了,那麼這個神經元的梯度就永遠都會是0。實際操作中,如果你的learning rate 很大,那麼很有可能你網路中的40%的神經元都”dead”了。 當然,如果你設定了一個合適的較小的learning rate(大的梯度流過一ReLU 神經元會變成小梯度,引數不會變得特別小,正向傳播時啟用就不一定為0了),這個問題發生的情況其實也不會太頻繁。ReLU units can be fragile during training and can “die”. For example, a large gradient flowing through a ReLU neuron could cause the weights to update in such a way that the neuron will never activate on any datapoint again. If this happens, then the gradient flowing through the unit will forever be zero from that point on. That is, the ReLU units can irreversibly die during training since they can get knocked off the data manifold. For example, you may find that as much as 40% of your network can be “dead” (i.e. neurons that never activate across the entire training dataset) if the learning rate is set too high. With a proper setting of the learning rate this is less frequently an issue. 或者這麼解釋:如果某次某個點梯度下降的非常多,權重被改變的特別多,那麼這個點的激勵可能永遠都是0了。
ReLU還經常被“詬病”的一個問題是輸出具有偏移現象,即輸出均值恆大於零。偏移現象和 神經元死亡會共同影響網路的收斂性。在arxiv的文章[Li, Y., et al., Improving Deep Neural Network with Multiple Parametric Exponential Linear Units. arXiv preprint arXiv:1606.00305, 2016.]中的實驗表明,如果不採用Batch Normalization,即使用 MSRA 初始化30層以上的ReLU網路,最終也難以收斂。相對的,PReLU和ELU網路都能順利收斂。
整流線性單元的三個擴充套件基於當 z i < 0 時使用一個非零的斜率 αi:hi=g(z,α)i=max(0,zi)+αimin(0,zi)
整流線性單元和它們的這些擴充套件都是基於一個原則,那就是如果它們的行為更接近線性,那麼模型更容易優化。使用線性行為更容易優化的一般性原則同樣也適用於除深度線性網路以外的情景。迴圈網路可以從序列中學習併產生狀態和輸出的序列。當訓練它們時,需要通過一些時間步來傳播資訊,當其中包含一些線性計算(具有大小接近 1 的某些方向導數)時,這會更容易。作為效能最好的迴圈網路結構之一,LSTM 通過求和在時間上傳播資訊,這是一種特別直觀的線性啟用。
絕對值整流(absolute value rectification)
固定 α i = −1 來得到 g(z) = |z|。它用於影象中的物件識別 (Jarrett et al., 2009a),其中尋找在輸入照明極性反轉下不變的特徵是有意義的。整流線性單元的其他擴充套件比這應用地更廣泛。
滲漏整流線性單元(Leaky ReLU)(Maas et al., 2013)
將 α i 固定成一個類似 0.01 的小值。
引數化整流線性單元PReLU
引數化整流線性單元(parametric ReLU)或者 PReLU 將α i 作為學習的引數 [He, K., et al. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. ICCV 2015.],具有非飽和性:


與LReLU相比,PReLU中的負半軸斜率a可學習而非固定。原文獻建議初始化a為0.25,不採用正則。個人認為,是否採用正則應當視具體的資料庫和網路,通常情況下使用正則能夠帶來效能提升。雖然PReLU 引入了額外的引數,但基本不需要擔心過擬合。例如,在上述cifar10+NIN實驗中, PReLU比ReLU和ELU多引入了引數,但也展現了更優秀的效能。所以實驗中若發現網路效能不好,建議從其他角度尋找原因。與ReLU相比,PReLU收斂速度更快。因為PReLU的輸出更接近0均值,使得SGD更接近natural gradient。證明過程參見原文[10]。此外,作者在ResNet 中採用ReLU,而沒有采用新的PReLU。這裡給出個人淺見,不一定正確,僅供參考。首先,在上述LReLU實驗中,負半軸斜率對效能的影響表現出一致性。對PReLU採用正則將啟用值推向0也能夠帶來效能提升。這或許表明,小尺度或稀疏啟用值對深度網路的影響更大。其次,ResNet中包含單位變換和殘差兩個分支。殘差分支用於學習對單位變換的擾動。如果單位變換是最優解,那麼殘差分支的擾動應該越小越好。這種假設下,小尺度或稀疏啟用值對深度網路的影響更大。此時,ReLU或許是比PReLU更好的選擇。
softplus函式
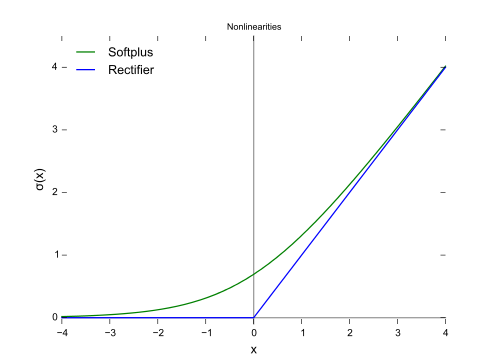
f(x)= ζ(x) =ln(1+ex)這是整流線性單元的平滑版本,由 Dugas et al. (2001b) 引入用於函式近似,由 Nair and Hinton (2010a) 引入用於無向概率模型的條件分佈。Glorot et al. (2011a) 比較了 softplus 和整流線性單元,發現後者的結果更好。通常不鼓勵使用 softplus 函式。softplus 表明隱藏單元型別的效能可能是非常反直覺的——因為它處處可導或者因為它不完全飽和,人們可能希望它具有優於整流線性單元的點,但根據經驗來看,它並沒有。
Maxout單元
Maxout[Goodfellow, I.J., et al. Maxout Networks. ICML 2013.]是ReLU的推廣,其發生飽和是一個零測集事件(measure zero event)。正式定義為:Maxout網路能夠近似任意連續函式,且當w2,b2,…,wn,bn為0時,退化為ReLU。 其實,Maxout的思想在視覺領域存在已久。例如,在HOG特徵裡有這麼一個過程:計算三個通道的梯度強度,然後在每一個畫素位置上,僅取三個通道中梯度強度最大的數值,最終形成一個通道。這其實就是Maxout的一種特例。
Note: lz每個神經元有多個不同輸入,求梯度時取最大。
Maxout能夠緩解梯度消失,同時又規避了ReLU神經元死亡的缺點,但增加了引數和計算量。




