歷屆試題 九宮重排 廣度優先搜尋+康拓排序
阿新 • • 發佈:2019-01-22
歷屆試題 九宮重排
時間限制:1.0s 記憶體限制:256.0MB
問題描述
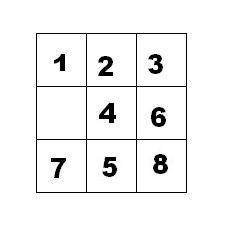
如下面第一個圖的九宮格中,放著 1~8 的數字卡片,還有一個格子空著。與空格子相鄰的格子中的卡片可以移動到空格中。經過若干次移動,可以形成第二個圖所示的局面。
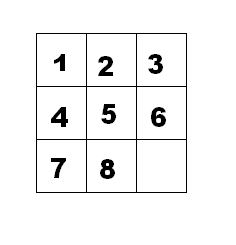
我們把第一個圖的局面記為:12345678.
把第二個圖的局面記為:123.46758
顯然是按從上到下,從左到右的順序記錄數字,空格記為句點。
本題目的任務是已知九宮的初態和終態,求最少經過多少步的移動可以到達。如果無論多少步都無法到達,則輸出-1。 輸入格式 輸入第一行包含九宮的初態,第二行包含九宮的終態。 輸出格式 輸出最少的步數,如果不存在方案,則輸出-1。 樣例輸入 12345678.
123.46758 樣例輸出 3 樣例輸入 13524678.
46758123. 樣例輸出 22
我們把第一個圖的局面記為:12345678.
把第二個圖的局面記為:123.46758
顯然是按從上到下,從左到右的順序記錄數字,空格記為句點。
本題目的任務是已知九宮的初態和終態,求最少經過多少步的移動可以到達。如果無論多少步都無法到達,則輸出-1。 輸入格式 輸入第一行包含九宮的初態,第二行包含九宮的終態。 輸出格式 輸出最少的步數,如果不存在方案,則輸出-1。 樣例輸入 12345678.
123.46758 樣例輸出 3 樣例輸入 13524678.
46758123. 樣例輸出 22
經典把數碼搜尋的題目,值得好好研究一下。
1,以前學的一門科目上的例題,用來講解深度搜索和廣度搜索的。
2,acm中也有很多類似的題目,這題可以採用a*演算法
3,大致的思路就是,結合優先佇列,康拓排序判斷重複,進行搜尋
4,urld是一定的方向,可以輸出自行模擬是否正確。
Java程式碼:
注意java優先佇列的用法,
import java.util.Arrays; import java.util.Comparator; import java.util.PriorityQueue; import java.util.Scanner; class MyComp implements Comparator<node> { @Override public int compare(node o1, node o2) { return o1.f-o2.f;///小的優先 } } class node { int a[][] = new int [3][3] ; int x=0; int y=0; String states ; int d; int w; int f;///估價函式f=d+w; public node(){ for(int i=0;i<3;i++)Arrays.fill(a[i],0) ; states = "" ; x=0; y=0; } }; public class Main { static int temp[][] = new int[3][3]; static int MAXN=1000000;///最多是9! static int fac[]={1,1,2,6,24,120,720,5040,40320,362880};///康拖展開判重0!1!2!3!4!5!6!7!8!9! static boolean vis[] = new boolean [MAXN];///標記 static int addx[]={-1,1,0,0}; static int addy[]={0,0,-1,1}; static int e;///目標狀態,cantor展開對應的值 public static void main(String[] args) { // TODO Auto-generated method stub Scanner in = new Scanner(System.in) ; int arry [] = new int[9] ; String cc ; cc = in.next() ; for(int i=0;i<9;i++){ if(cc.charAt(i)=='.')arry[i]=9; else arry[i]=cc.charAt(i)-'0'; } int k=0; node h = new node() ; for(int i=0;i<3;i++){ for(int j=0;j<3;j++){ h.a[i][j]=arry[k++]; if(h.a[i][j]==9){ h.x=i; h.y=j; } } } cc = in.next() ; int it=0; for(int i=0;i<3;i++){ for(int j=0;j<3;j++){ if(cc.charAt(it)=='.')temp[i][j]=9; else temp[i][j]=cc.charAt(it)-'0'; it++; } } ///判斷是否可解 int check [] = new int [9]; int c=0; for(int i=0;i<3;i++){ for(int j=0;j<3;j++){ if(h.a[i][j]==9)check[c++]=0; else check[c++]=h.a[i][j]; } } int sum1=0; for(int i=0;i<9;i++){ if(check[i]==0)continue; for(int j=0;j<i;j++){ if(check[j]>check[i]){ sum1++; } } } c=0; for(int i=0;i<3;i++){ for(int j=0;j<3;j++){ if(temp[i][j]==9)check[c++]=0; else check[c++]=temp[i][j]; } } int sum2=0; for(int i=0;i<9;i++){ if(check[i]==0)continue; for(int j=0;j<i;j++){ if(check[j]>check[i]){ sum2++; } } } if(sum1%2!=sum2%2){//開始狀態的逆序數和目標狀態的逆序數奇偶性不同,無解! System.out.println("-1"); return; } ///無解判斷結束 e = cantor(temp); Arrays.fill(vis, false); vis[cantor(h.a)]=true; PriorityQueue<node> qq = new PriorityQueue<node>(new MyComp()) ; qq.clear(); qq.offer(h) ; while(!qq.isEmpty()){ node top=qq.poll(); if(cantor(top.a)==e){ System.out.println(top.states.length()); return ; } int ch[][] = new int [3][3]; for(int i=0;i<3;i++){ for(int j=0;j<3;j++){ ch[i][j]=top.a[i][j]; } } for(int i=0;i<4;i++){ int newx=top.x+addx[i]; int newy=top.y+addy[i]; if(newx>=0&&newx<3&&newy>=0&&newy<3){ int tt = ch[newx][newy] ; ch[newx][newy] = ch[top.x][top.y] ; ch[top.x][top.y] = tt; if(!vis[cantor(ch)]){ node pp = new node(); for(int kk=0;kk<3;kk++){ for(int kkk=0;kkk<3;kkk++){ pp.a[kk][kkk] = ch[kk][kkk]; } } //memcpy(pp.states,top.states,sizeof(top.states)); pp.states = top.states ; pp.x=newx; pp.y=newy; pp.d=top.d+1; pp.w=get(ch); pp.f=pp.d+pp.w; if(i==0)pp.states+="u"; if(i==1)pp.states+="d"; if(i==2)pp.states+="l"; if(i==3)pp.states+="r"; if(pp.f<=100){ qq.offer(pp); vis[cantor(pp.a)]=true;} } //swap(ch[newx][newy],ch[top.x][top.y]); tt = ch[newx][newy] ; ch[newx][newy] = ch[top.x][top.y] ; ch[top.x][top.y] = tt; } } } } static int cantor(int m[][])///康拖展開求該序列的hash值 { int s[] = new int [9]; int k=0; for(int i=0;i<3;i++){ for(int j=0;j<3;j++){ s[k++]=m[i][j]; } } int sum=0; for(int i=0;i<9;i++) { int num=0; for(int j=i+1;j<9;j++) if(s[j]<s[i])num++; sum+=(num*fac[9-i-1]); } return sum+1; } static int get(int m[][]){///獲得開始狀態和目標狀態,“錯位個數” int ret=0; for(int i=0;i<3;i++){ for(int j=0;j<3;j++){ if(temp[i][j]!=m[i][j]){ ret++; } } } return ret; } }
