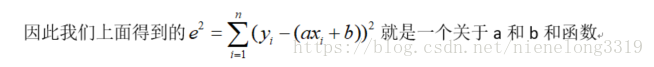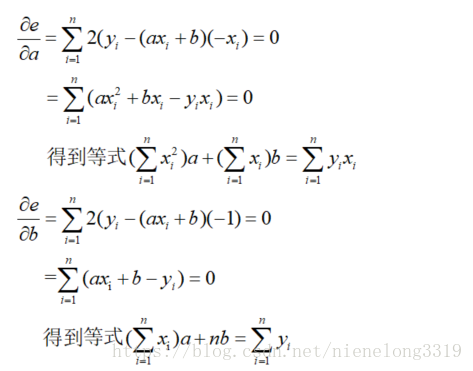opencv學習——最小二乘法擬合直線
阿新 • • 發佈:2019-01-22
最小二乘法擬合直線
概念:最小二乘法多項式直線擬合,根據給定的點,求出它的函式y=f(x),當然求得準確的函式是不太可能的,但是我們能求出它的近似曲線y=φ(x)
原理
假設有點 , I = 1,2,3,……n,求近似曲線y=φ(x),並且使得y=φ(x)與y=f(x)的平方偏差和最小,偏差
其中我們要找到一組最好的a b ,“最好的”就是要使選出的a b能使得所有的誤差達到最小化。
在此要注意以下,y=ax+b 這裡面的未知量是什麼,很自然的說法是x y,實際上並不是,我們不用去解這個x和y ,因為x和y已經是給定的值了,當我們在找這條直線的時候,我們實際上並不關心x的值有多好,我們要的就是a 和b這兩個變數,它們可以描述x和y之間的關係,我們就是在試圖找出那條最適合的直線所對應的a和b。
可以看到最小二乘法對各個變數求偏導,使得偏導值為0,即可得到最小值,因為e是關於a b的函式,導數為0的點必定是最小值,進入正題
分別對 a b求偏導可以得到:
關於solve函式 ,可以在這個連結檢視用法:solve函式使用
接下來上程式碼
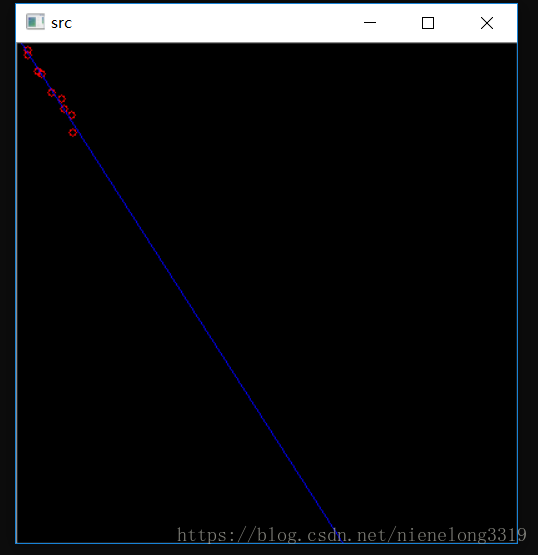
#include<iostream> #include<opencv2\opencv.hpp> using namespace std; using namespace cv; int main() { vector<Point>points; //(27 39) (8 5) (8 9) (16 22) (44 71) (35 44) (43 57) (19 24) (27 39) (37 52) points.push_back(Point(27, 39)); points.push_back(Point(8, 5)); points.push_back(Point(8, 9)); points.push_back(Point(16, 22)); points.push_back(Point(44, 71)); points.push_back(Point(35, 44)); points.push_back(Point(43, 57)); points.push_back(Point(19, 24)); points.push_back(Point(27, 39)); points.push_back(Point(37, 52)); Mat src = Mat::zeros(400, 400, CV_8UC3); for (int i = 0;i < points.size();i++) { //在原圖上畫出點 circle(src, points[i], 3, Scalar(0, 0, 255), 1, 8); } //構建A矩陣 int N = 2; Mat A = Mat::zeros(N, N, CV_64FC1); for (int row = 0;row < A.rows;row++) { for (int col = 0; col < A.cols;col++) { for (int k = 0;k < points.size();k++) { A.at<double>(row, col) = A.at<double>(row, col) + pow(points[k].x, row + col); } } } //構建B矩陣 Mat B = Mat::zeros(N, 1, CV_64FC1); for (int row = 0;row < B.rows;row++) { for (int k = 0;k < points.size();k++) { B.at<double>(row, 0) = B.at<double>(row, 0) + pow(points[k].x, row)*points[k].y; } } //A*X=B Mat X; //cout << A << endl << B << endl; solve(A, B, X,DECOMP_LU); cout << X << endl; vector<Point>lines; for (int x = 0;x < src.size().width;x++) { // y = b + ax; double y = X.at<double>(0, 0) + X.at<double>(1, 0)*x; printf("(%d,%lf)\n", x, y); lines.push_back(Point(x, y)); } polylines(src, lines, false, Scalar(255, 0, 0), 1, 8); imshow("src", src); //imshow("src", A); waitKey(0); return 0; }
可以看到如下結果