一．課程網址及成績記錄

2、評分標準：三個單元測驗分別為第1、2章，第3、4、5章，第6、7章，各佔15%，論壇討論佔5％，期末考試佔50%，按百分制計分，60分至84分為合格，85分至100分為優秀。

3、需要說明一下的是單元測試每一次總分為30分，期末考試總分是50分。因為是7月6號課程才結束，所以現在還不可以申請證書。現在只能貼出每一次的小練習的分數和期末考試的分數。

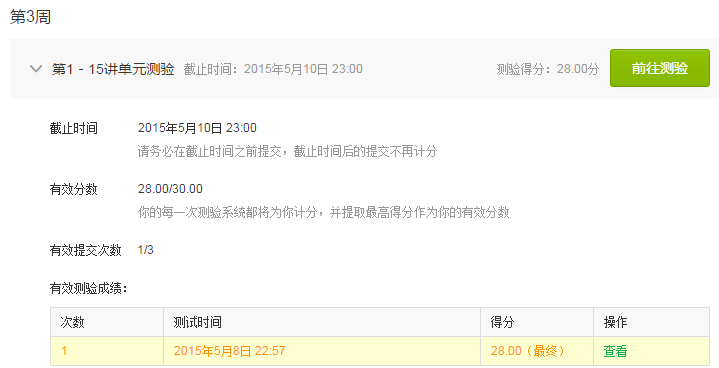
第1－15講單元測驗

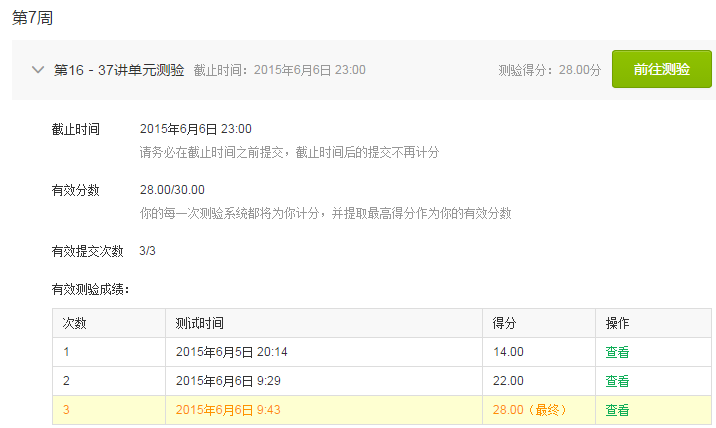
第16－37講單元測驗

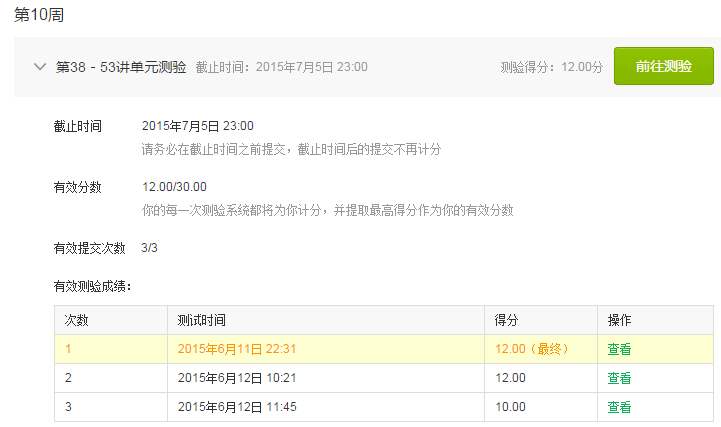
第38－53講單元測驗

《概率論與數理統計》期末考試

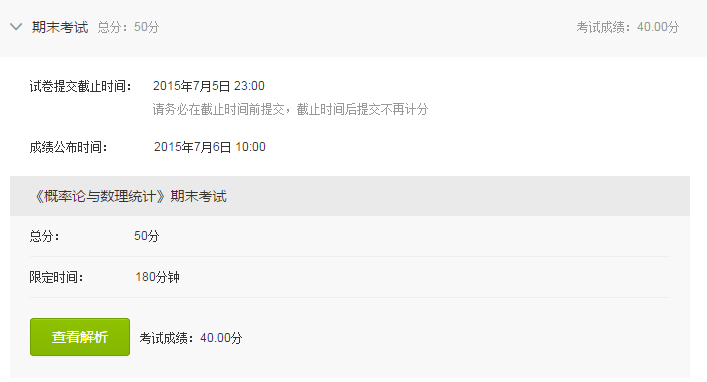
最終的成績：（28/30+28/30+12/30)*100*0.15+(40/50)*100*0.5+5=79

一．選擇概率論與數理統計的原因

其實一開始當老師說可以在MOOC上選擇自己喜歡的課程的時候，我是有點驚訝的。因為從小到大給我的觀念就是在學校上什麼課程都是固定而且被動的（選修課除外），而丁又專老師的這門課讓我有了新的認識。自己仔細想想也對，雖然說在課堂上學習的內容與符合專業的大方向，目的性很強。但是它也有它的侷限性。主要包括：第一點，時間的侷限性，只能在學校安排的時間學習；第二點，空間的侷限性，學習的地方只限於教室等等。而MOOC就是為了解決這些問題應運而生的。它最大的特點就是無論何時何地，只要你想，都能夠學。

至於我為什麼要學概率論，主要是一來這一兩年來學理論的東西太多了，很多東西要背，腦子都快有點轉不動了，所以就想找一個課程，純粹只是想做一些題鍛鍊鍛鍊思維來中和一下，免得大腦打結；二來我想試試自己的控制能力，因為MOOC

二．課程的學習收穫

一個課程下來我基本上掌握了

1.概率論部分：

(1)常見分佈列，分佈函式：離散型--連續型 一維--二維； 離散：兩點分佈，二次分佈，泊松分佈，幾何分佈；連續：均勻分佈，指數分佈，正態分佈。

(2)基本運算概念：概率密度，數學期望，方差，協方差，相關係數。 

2.數理統計部分：

(1)樣本基本概念： χ2分佈，t分佈，F分佈，正態總體的樣本均值，方差，k階原點矩，k階中心矩。

(2)引數估計：點估計，矩估計，最大似然估計法，無偏性，有效性，區間等。

概率論前幾周的課程都是以簡單的概率計算為主，因為在高中已經接觸過，所以學起來比較輕鬆。簡單的概率計算基本上都可以由幾個基本公式（比如：全概率公式，貝葉斯公式，條件概率公式，乘法公式）得到。接下來接觸到了幾個重要的函式，分佈函式，密度函式等，研究的物件也從原先的離散型隨機變數擴充套件為連續性隨機變數。我覺得相對來說比較抽象，需要搞清楚分佈律、概率密度、分佈函式的定義、性質、用途和關係，花的時間也比前面多了，前面的視訊可以有選擇性的跳過，到這裡就時不時就需要停頓一下，開始做一些必要的筆記，好好理解一番。再後來是數理統計部分，這部分內容比較難，偏記憶的知識點較多，很容易混淆，好比如估計理論，我一開始就經常把總體引數和樣本引數混淆。還有就是結論多，計算繁瑣，好像通過樣本來估計某個總體引數所在的區間，矩估計和最大似然估計量這類的計算要一大堆，導致我現在還沒有好好的摸透它。

四．感受與體會

在學習中，遇到很困擾的問題就是很多概念性的定義或者知識看不懂或容易忘記。後來我想了一個辦法就是老師講了一遍之後，如果還是不明白的話就再看一篇，然後自己在腦海在試著勾勒出那個概念或知識的來龍去脈，這樣理解性記憶減輕了不少負擔。

概率統計並不是給你一個數學題目讓你算出一個相應的結果。它是真正把實際為題轉化為數學問題的學問，因為它解決的並不是單純的數學問題，而是給你一個命題讓你去設想構思，進而把想法應用到解決實際問題上，很貼近實際。比如抽獎先後中獎概率都一樣，扔硬幣為什麼正反面的概率都是二分之一等。一些問題還會讓我們更理性的對待實際中的一些問題，比如賭博贏的概率很小，彩票中獎概率也是微乎其微，所以不能迷戀那些，不能期望用投機取巧來賺取錢財等等。

概率論與數理統計入門容易，但是要理解透徹比較困難。有句話說得好，基礎學科學時覺無用，用時方恨少。對於此，我還有很長一段路要走。