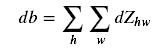Convolutional Neural Networks: Step by Step

Welcome to Course 4's first assignment! In this assignment, you will implement convolutional (CONV) and pooling (POOL) layers in numpy, including both forward propagation and (optionally) backward propagation.

Notation:

We assume that you are already familiar with numpy and/or have completed the previous courses of the specialization. Let's get started!

1 - Packages

Let's first import all the packages that you will need during this assignment.

• numpy is the fundamental package for scientific computing with Python.
• matplotlib is a library to plot graphs in Python.
• np.random.seed(1) is used to keep all the random function calls consistent. It will help us grade your work.

import numpy as np
import h5py
import matplotlib.pyplot as plt

%matplotlib inline
plt.rcParams['figure.figsize'] = (5.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

%load_ext autoreload
%autoreload 2

np.random.seed(1)

2 - Outline of the Assignment

You will be implementing the building blocks of a convolutional neural network! Each function you will implement will have detailed instructions that will walk you through the steps needed:

• Convolution functions, including:
  • Zero Padding
  • Convolve window
  • Convolution forward
  • Convolution backward (optional)
• Pooling functions, including:
  • Pooling forward
  • Create mask
  • Distribute value
  • Pooling backward (optional)

This notebook will ask you to implement these functions from scratch in numpy. In the next notebook, you will use the TensorFlow equivalents of these functions to build the following model:

Note that for every forward function, there is its corresponding backward equivalent. Hence, at every step of your forward module you will store some parameters in a cache. These parameters are used to compute gradients during backpropagation.

3 - Convolutional Neural Networks

Although programming frameworks make convolutions easy to use, they remain one of the hardest concepts to understand in Deep Learning. A convolution layer transforms an input volume into an output volume of different size, as shown below.

In this part, you will build every step of the convolution layer. You will first implement two helper functions: one for zero padding and the other for computing the convolution function itself.

3.1 - Zero-Padding

Zero-padding adds zeros around the border of an image:

Figure 1 : Zero-Padding
Image (3 channels, RGB) with a padding of 2.

The main benefits of padding are the following:

• It allows you to use a CONV layer without necessarily shrinking the height and width of the volumes. This is important for building deeper networks, since otherwise the height/width would shrink as you go to deeper layers. An important special case is the "same" convolution, in which the height/width is exactly preserved after one layer.

• It helps us keep more of the information at the border of an image. Without padding, very few values at the next layer would be affected by pixels as the edges of an image.

Exercise: Implement the following function, which pads all the images of a batch of examples X with zeros. Use np.pad. Note if you want to pad the array "a" of shape(5,5,5,5,5)with pad = 1 for the 2nd dimension, pad = 3 for the 4th dimension and pad = 0 for the rest, you would do:

a = np.pad(a, ((0,0), (1,1), (0,0), (3,3), (0,0)), 'constant', constant_values = (..,..))

# GRADED FUNCTION: zero_pad

def zero_pad(X, pad):
    """
    Pad with zeros all images of the dataset X. The padding is applied to the height and width of an image, 
    as illustrated in Figure 1.
    
    Argument:
    X -- python numpy array of shape (m, n_H, n_W, n_C) representing a batch of m images
    pad -- integer, amount of padding around each image on vertical and horizontal dimensions
    
    Returns:
    X_pad -- padded image of shape (m, n_H + 2*pad, n_W + 2*pad, n_C)
    """
    
    ### START CODE HERE ### (≈ 1 line)
    X_pad = np.pad(X,((0,0),(pad,pad),(pad,pad),(0,0)),'constant',constant_values=(0,0))
    ### END CODE HERE ###
    
    return X_pad

np.random.seed(1)
x = np.random.randn(4, 3, 3, 2)
x_pad = zero_pad(x, 2)
print ("x.shape =", x.shape)
print ("x_pad.shape =", x_pad.shape)
print ("x[1,1] =", x[1,1])
print ("x_pad[1,1] =", x_pad[1,1])

fig, axarr = plt.subplots(1, 2)
axarr[0].set_title('x')
axarr[0].imshow(x[0,:,:,0])
axarr[1].set_title('x_pad')
axarr[1].imshow(x_pad[0,:,:,0])

x.shape = (4, 3, 3, 2)
x_pad.shape = (4, 7, 7, 2)
x[1,1] = [[ 0.90085595 -0.68372786]
 [-0.12289023 -0.93576943]
 [-0.26788808  0.53035547]]
x_pad[1,1] = [[ 0.  0.]
 [ 0.  0.]
 [ 0.  0.]
 [ 0.  0.]
 [ 0.  0.]
 [ 0.  0.]
 [ 0.  0.]]

Out[3]:

<matplotlib.image.AxesImage at 0x7f8fbf27f160>

Expected Output:

x.shape:	(4, 3, 3, 2)
x_pad.shape:	(4, 7, 7, 2)
x[1,1]:	[[ 0.90085595 -0.68372786] [-0.12289023 -0.93576943] [-0.26788808 0.53035547]]
x_pad[1,1]:	[[ 0. 0.] [ 0. 0.] [ 0. 0.] [ 0. 0.] [ 0. 0.] [ 0. 0.] [ 0. 0.]]

3.2 - Single step of convolution

In this part, implement a single step of convolution, in which you apply the filter to a single position of the input. This will be used to build a convolutional unit, which:

• Takes an input volume
• Applies a filter at every position of the input
• Outputs another volume (usually of different size)

Figure 2 : Convolution operation
with a filter of 2x2 and a stride of 1 (stride = amount you move the window each time you slide)

In a computer vision application, each value in the matrix on the left corresponds to a single pixel value, and we convolve a 3x3 filter with the image by multiplying its values element-wise with the original matrix, then summing them up and adding a bias. In this first step of the exercise, you will implement a single step of convolution, corresponding to applying a filter to just one of the positions to get a single real-valued output.

Later in this notebook, you'll apply this function to multiple positions of the input to implement the full convolutional operation.

Exercise: Implement conv_single_step(). Hint.

# GRADED FUNCTION: conv_single_step

def conv_single_step(a_slice_prev, W, b):
    """
    Apply one filter defined by parameters W on a single slice (a_slice_prev) of the output activation 
    of the previous layer.
    
    Arguments:
    a_slice_prev -- slice of input data of shape (f, f, n_C_prev)
    W -- Weight parameters contained in a window - matrix of shape (f, f, n_C_prev)
    b -- Bias parameters contained in a window - matrix of shape (1, 1, 1)
    
    Returns:
    Z -- a scalar value, result of convolving the sliding window (W, b) on a slice x of the input data
    """

    ### START CODE HERE ### (≈ 2 lines of code)
    # Element-wise product between a_slice and W. Do not add the bias yet.
    s = W*a_slice_prev
    # Sum over all entries of the volume s.
    Z = np.sum(s)
    # Add bias b to Z. Cast b to a float() so that Z results in a scalar value.
    Z = Z + float(b)
    ### END CODE HERE ###

    return Z

np.random.seed(1)
a_slice_prev = np.random.randn(4, 4, 3)
W = np.random.randn(4, 4, 3)
b = np.random.randn(1, 1, 1)

Z = conv_single_step(a_slice_prev, W, b)
print("Z =", Z)

Z = -6.99908945068

Expected Output:

Z	-6.99908945068

3.3 - Convolutional Neural Networks - Forward pass

In the forward pass, you will take many filters and convolve them on the input. Each 'convolution' gives you a 2D matrix output. You will then stack these outputs to get a 3D volume:

Exercise: Implement the function below to convolve the filters W on an input activation A_prev. This function takes as input A_prev, the activations output by the previous layer (for a batch of m inputs), F filters/weights denoted by W, and a bias vector denoted by b, where each filter has its own (single) bias. Finally you also have access to the hyperparameters dictionary which contains the stride and the padding.

Hint:

1. To select a 2x2 slice at the upper left corner of a matrix "a_prev" (shape (5,5,3)), you would do:

   a_slice_prev = a_prev[0:2,0:2,:]
   

   This will be useful when you will define a_slice_prev below, using the start/end indexes you will define.
2. To define a_slice you will need to first define its corners vert_start, vert_end, horiz_start and horiz_end. This figure may be helpful for you to find how each of the corner can be defined using h, w, f and s in the code below.

Figure 3 : Definition of a slice using vertical and horizontal start/end (with a 2x2 filter) 
This figure shows only a single channel.

Reminder: The formulas relating the output shape of the convolution to the input shape is:

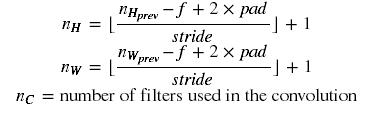For this exercise, we won't worry about vectorization, and will just implement everything with for-loops.

# GRADED FUNCTION: conv_forward

def conv_forward(A_prev, W, b, hparameters):
    """
    Implements the forward propagation for a convolution function
    
    Arguments:
    A_prev -- output activations of the previous layer, numpy array of shape (m, n_H_prev, n_W_prev, n_C_prev)
    W -- Weights, numpy array of shape (f, f, n_C_prev, n_C)
    b -- Biases, numpy array of shape (1, 1, 1, n_C)
    hparameters -- python dictionary containing "stride" and "pad"
        
    Returns:
    Z -- conv output, numpy array of shape (m, n_H, n_W, n_C)
    cache -- cache of values needed for the conv_backward() function
    """
    
    ### START CODE HERE ###
    # Retrieve dimensions from A_prev's shape (≈1 line)  
    (m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
    
    # Retrieve dimensions from W's shape
    (f,f,n_C_prev,n_C) = W.shape
    
    # Retrieve information from "hparameters" (≈2 lines)
    stride = hparameters["stride"]
    pad = hparameters["pad"]
    
    # Compute the dimensions of the CONV output volume using the formula given above. Hint: use int() to floor. (≈2 lines)
    n_H = int((n_H_prev+2*pad-f)/stride)+1
    n_W = int((n_W_prev+2*pad-f)/stride)+1
    
    # Initialize the output volume Z with zeros. (≈1 line)
    Z = np.zeros((m,n_H,n_W,n_C))
    
    # Create A_prev_pad by padding A_prev
    A_prev_pad = zero_pad(A_prev,pad)
    
    for i in range(m):                                 # loop over the batch of training examples
        a_prev_pad = A_prev_pad[i,:,:,:]                     # Select ith training example's padded activation
        for h in range(n_H):                           # loop over vertical axis of the output volume
            for w in range(n_W):                       # loop over horizontal axis of the output volume
                for c in range(n_C):                   # loop over channels (= #filters) of the output volume
                    
                    # Find the corners of the current "slice" (≈4 lines)
                    vert_start = h*stride
                    vert_end = h*stride+f
                    horiz_start = w*stride
                    horiz_end = w*stride+f
                    
                    # Use the corners to define the (3D) slice of a_prev_pad (See Hint above the cell). (≈1 line)
                    a_slice_prev = a_prev_pad[vert_start:vert_end,horiz_start:horiz_end,:]
                    # Convolve the (3D) slice with the correct filter W and bias b, to get back one output neuron. (≈1 line)
                    Z[i, h, w, c] = conv_single_step(a_slice_prev,W[:,:,:,c],b[:,:,:,c])
                                        
    ### END CODE HERE ###
    
    # Making sure your output shape is correct
    assert(Z.shape == (m, n_H, n_W, n_C))
    
    # Save information in "cache" for the backprop
    cache = (A_prev, W, b, hparameters)
    
    return Z, cache

np.random.seed(1)
A_prev = np.random.randn(10,4,4,3)
W = np.random.randn(2,2,3,8)
b = np.random.randn(1,1,1,8)
hparameters = {"pad" : 2,
               "stride": 2}

Z, cache_conv = conv_forward(A_prev, W, b, hparameters)
print("Z's mean =", np.mean(Z))
print("Z[3,2,1] =", Z[3,2,1])
print("cache_conv[0][1][2][3] =", cache_conv[0][1][2][3])

Z's mean = 0.0489952035289
Z[3,2,1] = [-0.61490741 -6.7439236  -2.55153897  1.75698377  3.56208902  0.53036437
  5.18531798  8.75898442]
cache_conv[0][1][2][3] = [-0.20075807  0.18656139  0.41005165]

Expected Output:

Z's mean	0.0489952035289
Z[3,2,1]	[-0.61490741 -6.7439236 -2.55153897 1.75698377 3.56208902 0.53036437 5.18531798 8.75898442]
cache_conv[0][1][2][3]	[-0.20075807 0.18656139 0.41005165]

Finally, CONV layer should also contain an activation, in which case we would add the following line of code:

# Convolve the window to get back one output neuron
Z[i, h, w, c] = ...
# Apply activation
A[i, h, w, c] = activation(Z[i, h, w, c])

You don't need to do it here.

4 - Pooling layer

The pooling (POOL) layer reduces the height and width of the input. It helps reduce computation, as well as helps make feature detectors more invariant to its position in the input. The two types of pooling layers are:

• Max-pooling layer: slides an (f,f) window over the input and stores the max value of the window in the output.

• Average-pooling layer: slides an (f,f) window over the input and stores the average value of the window in the output.

These pooling layers have no parameters for backpropagation to train. However, they have hyperparameters such as the window size ff. This specifies the height and width of the fxf window you would compute a max or average over.

4.1 - Forward Pooling

Now, you are going to implement MAX-POOL and AVG-POOL, in the same function.

Exercise: Implement the forward pass of the pooling layer. Follow the hints in the comments below.

Reminder: As there's no padding, the formulas binding the output shape of the pooling to the input shape is:

# GRADED FUNCTION: pool_forward

def pool_forward(A_prev, hparameters, mode = "max"):
    """
    Implements the forward pass of the pooling layer
    
    Arguments:
    A_prev -- Input data, numpy array of shape (m, n_H_prev, n_W_prev, n_C_prev)
    hparameters -- python dictionary containing "f" and "stride"
    mode -- the pooling mode you would like to use, defined as a string ("max" or "average")
    
    Returns:
    A -- output of the pool layer, a numpy array of shape (m, n_H, n_W, n_C)
    cache -- cache used in the backward pass of the pooling layer, contains the input and hparameters 
    """
    
    # Retrieve dimensions from the input shape
    (m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
    
    # Retrieve hyperparameters from "hparameters"
    f = hparameters["f"]
    stride = hparameters["stride"]
    
    # Define the dimensions of the output
    n_H = int(1 + (n_H_prev - f) / stride)
    n_W = int(1 + (n_W_prev - f) / stride)
    n_C = n_C_prev
    
    # Initialize output matrix A
    A = np.zeros((m, n_H, n_W, n_C))              
    
    ### START CODE HERE ###
    for i in range(m):                         # loop over the training examples
        for h in range(n_H):                     # loop on the vertical axis of the output volume
            for w in range(n_W):                 # loop on the horizontal axis of the output volume
                for c in range (n_C):            # loop over the channels of the output volume
                    
                    # Find the corners of the current "slice" (≈4 lines)
                    vert_start = h*stride
                    vert_end = h*stride + f
                    horiz_start = w*stride
                    horiz_end = w*stride + f
                    
                    # Use the corners to define the current slice on the ith training example of A_prev, channel c. (≈1 line)
                    a_prev_slice = A_prev[i,vert_start:vert_end,horiz_start:horiz_end,c]
                    
                    # Compute the pooling operation on the slice. Use an if statment to differentiate the modes. Use np.max/np.mean.
                    if mode == "max":
                        A[i, h, w, c] = np.max(a_prev_slice)
                    elif mode == "average":
                        A[i,h,w,c]=np.mean(a_prev_slice)
    
    ### END CODE HERE ###
    
    # Store the input and hparameters in "cache" for pool_backward()
    cache = (A_prev, hparameters)
    
    # Making sure your output shape is correct
    assert(A.shape == (m, n_H, n_W, n_C))
    
    return A, cache

np.random.seed(1)
A_prev = np.random.randn(2, 4, 4, 3)
hparameters = {"stride" : 2, "f": 3}

A, cache = pool_forward(A_prev, hparameters)
print("mode = max")
print("A =", A)
print()
A, cache = pool_forward(A_prev, hparameters, mode = "average")
print("mode = average")
print("A =", A)

mode = max
A = [[[[ 1.74481176  0.86540763  1.13376944]]]


 [[[ 1.13162939  1.51981682  2.18557541]]]]

mode = average
A = [[[[ 0.02105773 -0.20328806 -0.40389855]]]


 [[[-0.22154621  0.51716526  0.48155844]]]]

Expected Output:

A =	[[[[ 1.74481176 0.86540763 1.13376944]]] [[[ 1.13162939 1.51981682 2.18557541]]]]
A =	[[[[ 0.02105773 -0.20328806 -0.40389855]]] [[[-0.22154621 0.51716526 0.48155844]]]]

Congratulations! You have now implemented the forward passes of all the layers of a convolutional network.

The remainer of this notebook is optional, and will not be graded.

5 - Backpropagation in convolutional neural networks (OPTIONAL / UNGRADED)

In modern deep learning frameworks, you only have to implement the forward pass, and the framework takes care of the backward pass, so most deep learning engineers don't need to bother with the details of the backward pass. The backward pass for convolutional networks is complicated. If you wish however, you can work through this optional portion of the notebook to get a sense of what backprop in a convolutional network looks like.

When in an earlier course you implemented a simple (fully connected) neural network, you used backpropagation to compute the derivatives with respect to the cost to update the parameters. Similarly, in convolutional neural networks you can to calculate the derivatives with respect to the cost in order to update the parameters. The backprop equations are not trivial and we did not derive them in lecture, but we briefly presented them below.

5.1 - Convolutional layer backward pass

Let's start by implementing the backward pass for a CONV layer.

5.1.1 - Computing dA:

This is the formula for computing dA with respect to the cost for a certain filter Wcand a given training example:

Where Wc is a filter and dZhwis a scalar corresponding to the gradient of the cost with respect to the output of the conv layer Z at the hth row and wth column (corresponding to the dot product taken at the ith stride left and jth stride down). Note that at each time, we multiply the the same filter Wcby a different dZ when updating dA. We do so mainly because when computing the forward propagation, each filter is dotted and summed by a different a_slice. Therefore when computing the backprop for dA, we are just adding the gradients of all the a_slices.

In code, inside the appropriate for-loops, this formula translates into:

da_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :] += W[:,:,:,c] * dZ[i, h, w, c]

5.1.2 - Computing dW:

This is the formula for computing dWc(dWc is the derivative of one filter) with respect to the loss:

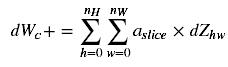
In code, inside the appropriate for-loops, this formula translates into:

dW[:,:,:,c] += a_slice * dZ[i, h, w, c]

5.1.3 - Computing db:

This is the formula for computing db with respect to the cost for a certain filter Wc:

As you have previously seen in basic neural networks, db is computed by summing dZ. In this case, you are just summing over all the gradients of the conv output (Z) with respect to the cost.

In code, inside the appropriate for-loops, this formula translates into:

db[:,:,:,c] += dZ[i, h, w, c]

Exercise: Implement the conv_backward function below. You should sum over all the training examples, filters, heights, and widths. You should then compute the derivatives using formulas 1, 2 and 3 above.

def conv_backward(dZ, cache):
    """
    Implement the backward propagation for a convolution function
    
    Arguments:
    dZ -- gradient of the cost with respect to the output of the conv layer (Z), numpy array of shape (m, n_H, n_W, n_C)
    cache -- cache of values needed for the conv_backward(), output of conv_forward()
    
    Returns:
    dA_prev -- gradient of the cost with respect to the input of the conv layer (A_prev),
               numpy array of shape (m, n_H_prev, n_W_prev, n_C_prev)
    dW -- gradient of the cost with respect to the weights of the conv layer (W)
          numpy array of shape (f, f, n_C_prev, n_C)
    db -- gradient of the cost with respect to the biases of the conv layer (b)
          numpy array of shape (1, 1, 1, n_C)
    """
    
    ### START CODE HERE ###
    # Retrieve information from "cache"
    (A_prev, W, b, hparameters) = cache
    
    # Retrieve dimensions from A_prev's shape
    (m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
    
    # Retrieve dimensions from W's shape
    (f, f, n_C_prev, n_C) = W.shape
    
    # Retrieve information from "hparameters"
    stride = hparameters["stride"]
    pad = hparameters["pad"]
    
    # Retrieve dimensions from dZ's shape
    (m, n_H, n_W, n_C) = dZ.shape
    
    # Initialize dA_prev, dW, db with the correct shapes
    dA_prev = np.zeros((A_prev.shape))                           
    dW = np.zeros((W.shape))
    db = np.zeros((1,1,1,n_C))

    # Pad A_prev and dA_prev
    A_prev_pad = zero_pad(A_prev,pad)
    dA_prev_pad = zero_pad(dA_prev,pad)
    for i in range(m):                       # loop over the training examples
        
        # select ith training example from A_prev_pad and dA_prev_pad
        a_prev_pad = A_prev_pad[i,:,:,:]
        da_prev_pad = dA_prev_pad[i,:,:,:]
        
        for h in range(n_H):                   # loop over vertical axis of the output volume
            for w in range(n_W):               # loop over horizontal axis of the output volume
                for c in range(n_C):           # loop over the channels of the output volume
                    
                    # Find the corners of the current "slice"
                    vert_start = h*stride
                    vert_end = h*stride+f
                    horiz_start = w*stride
                    horiz_end = w*stride+f
                    
                    # Use the corners to define the slice from a_prev_pad
                    a_slice = a_prev_pad[vert_start:vert_end,horiz_start:horiz_end,:]

                    # Update gradients for the window and the filter's parameters using the code formulas given above
                    da_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :] += W[:,:,:,c]*dZ[i,h,w,c]
                    dW[:,:,:,c] += a_slice*dZ[i,h,w,c]
                    db[:,:,:,c] += dZ[i,h,w,c]
                    
        # Set the ith training example's dA_prev to the unpaded da_prev_pad (Hint: use X[pad:-pad, pad:-pad, :])
        dA_prev[i, :, :, :] = da_prev_pad[pad:-pad,pad:-pad,:]
    ### END CODE HERE ###
    
    # Making sure your output shape is correct
    assert(dA_prev.shape == (m, n_H_prev, n_W_prev, n_C_prev))
    
    return dA_prev, dW, db

np.random.seed(1)
dA, dW, db = conv_backward(Z, cache_conv)
print("dA_mean =", np.mean(dA))
print("dW_mean =", np.mean(dW))
print("db_mean =", np.mean(db))

dA_mean = 1.45243777754
dW_mean = 1.72699145831
db_mean = 7.83923256462

Expected Output:

dA_mean	1.45243777754
dW_mean	1.72699145831
db_mean	7.83923256462

5.2 Pooling layer - backward pass

Next, let's implement the backward pass for the pooling layer, starting with the MAX-POOL layer. Even though a pooling layer has no parameters for backprop to update, you still need to backpropagation the gradient through the pooling layer in order to compute gradients for layers that came before the pooling layer.

5.2.1 Max pooling - backward pass

Before jumping into the backpropagation of the pooling layer, you are going to build a helper function called create_mask_from_window() which does the following:

As you can see, this function creates a "mask" matrix which keeps track of where the maximum of the matrix is. True (1) indicates the position of the maximum in X, the other entries are False (0). You'll see later that the backward pass for average pooling will be similar to this but using a different mask.

Exercise: Implement create_mask_from_window(). This function will be helpful for pooling backward. Hints:

• np.max() may be helpful. It computes the maximum of an array.
• If you have a matrix X and a scalar x: A = (X == x) will return a matrix A of the same size as X such that:

  A[i,j] = True if X[i,j] = x
  A[i,j] = False if X[i,j] != x
  

• Here, you don't need to consider cases where there are several maxima in a matrix.

            
  
           

              
              
            
            
相關推薦
			   
            
            
            
 

    

    
    
Deeplearning-吳恩達-卷積神經網路-第一週作業01-Convolution Networks(python)
     
 
                
Convolutional Neural Networks: Step by StepWelcome to Course 4's first assignment! In this assignment, you will implement convolutional ( 

  
 

    

    
    
吳恩達卷積神經網路——深度卷積網路：例項探究
     
  
  
  
 經典網路 
 LeNet5 
  隨著網路的加深，影象的高度和寬度在縮小，通道數量增加 池化後使用sigmoid函式 
 AlexNet 
  與LeNet相似，但大得多 使用ReLu函式 
 VGG-16 
  網路大，但結構並不複雜 影象縮小的比例和通道增加的比例是有規律的 64-> 

  
 

    

    
    
吳恩達卷積神經網路——卷積神經網路
     
  
  
  
 計算機視覺 
 相關問題： 1）影象分類：  2）目標檢測：  3）影象風格遷移：  挑戰：資料輸入可能會非常大 輸入10001000的彩色影象，則需要輸入的資料量為100010003 =3M，這意味著特徵向量X的維度高達3M ，如果在第一隱藏層有1000個神經元，使用標準全連線，那麼權值矩 

  
 

    

    
    
第4門課程-卷積神經網路-第二週作業1-基於Keras的人臉表情分類
     
 
							
							
							0- 背景：

從人臉影象中的表情判斷一個人是否快樂。本文將基於Keras實現該功能。Keras是一個更高階的API，其底層框架可以是TensorFlow或者CNTK。

1-資料載入：

匯入依賴的庫：

import numpy as np
#import  

  
 

    

    
    
吳恩達深度學習筆記（deeplearning.ai）之卷積神經網路（CNN）（上）
     
 
                

1. Padding

在卷積操作中，過濾器（又稱核）的大小通常為奇數，如3x3，5x5。這樣的好處有兩點：


	在特徵圖（二維卷積）中就會存在一箇中心畫素點。有一箇中心畫素點會十分方便，便於指出過濾器的位置。
	
	在沒有padding的情況下，經過卷積操作，輸出的資 

  
 

    

    
    
【Coursera】吳恩達 deeplearning.ai 04.卷積神經網路 第二週 深度卷積神經網路 課程筆記
     
  
 
  
  
 深度卷積神經網路 
 2.1 為什麼要進行例項化 
 實際上，在計算機視覺任務中表現良好的神經網路框架，往往也適用於其他任務。 
 2.2 經典網路 
  
  LeNet-5 
  AlexNet 
  VGG 
  
 LeNet-5 
 主要針對灰度影象   
 隨著神經網路的加深 

  
 

    

    
    
吳恩達Coursera深度學習課程 deeplearning.ai (4-1) 卷積神經網路--程式設計作業
     
 
							
							
							Part 1：卷積神經網路

本週課程將利用numpy實現卷積層(CONV) 和 池化層(POOL), 包含前向傳播和可選的反向傳播。



變數說明


上標[l][l] 表示神經網路的第幾層
上標(i)(i) 表示第幾個樣本
上標[i][i] 表示第幾個mi 

  
 

    

    
    
吳恩達Coursera深度學習課程 deeplearning.ai (4-1) 卷積神經網路--課程筆記
     
 
							
							
							本課主要講解了卷積神經網路的基礎知識，包括卷積層基礎（卷積核、Padding、Stride），卷積神經網路的基礎：卷積層、池化層、全連線層。



主要知識點


卷積核: 過濾器，各元素相乘再相加
nxn * fxf -> (n-f+1)x(n-f+1) 

  
 

    

    
    
Deeplearning.ai吳恩達筆記之神經網路和深度學習1
     
  
 
  
  
 Introduction to Deep Learning 
 What is a neural neural network? 
  
 當對於房價進行預測時，因為我們知道房子價格是不可能會有負數的，因此我們讓面積小於某個值時，價格始終為零。 
 其實對於以上這麼一個預測的模型就可以看 

  
 

    

    
    
Deeplearning.ai吳恩達筆記之神經網路和深度學習3
     
  
 
  
  
 Shallow Neural Network 
 Neural Networks Overview 
  
 同樣，反向傳播過程也分成兩層。第一層是輸出層到隱藏層，第二層是隱藏層到輸入層。其細節部分我們之後再來討論。 
 Neural Network Representation 
   

  
 

    

    
    
吳恩達機器學習 - 神經網路的反向傳播演算法 吳恩達機器學習 - 神經網路的反向傳播演算法
     
  
  
  
  
   
    
     
     原 
     吳恩達機器學習 - 神經網路的反向傳播演算法 
     
     
      
      2018年06月21日 20:59:35 
      離殤灬孤狼 
      閱讀數：373 
      											 

  
 

    

    
    
吳恩達機器學習 - 神經網路 吳恩達機器學習 - 神經網路
     
  
  
  
  
   
    
     
     原 
     吳恩達機器學習 - 神經網路 
     
     
      
      2018年06月19日 21:27:17 
      離殤灬孤狼 
      閱讀數：97 
      																				 

  
 

    

    
    
吳恩達改善深層神經網路引數：超引數除錯、正則化以及優化——優化演算法
     
  
  
  
 機器學習的應用是一個高度依賴經驗的過程，伴隨著大量的迭代過程，你需要訓練大量的模型才能找到合適的那個，優化演算法能夠幫助你快速訓練模型。 
 難點：機器學習沒有在大資料發揮最大的作用，我們可以利用巨大的資料集來訓練網路，但是在大資料下訓練網路速度很慢； 
 使用快速的優化演算法大大提高效率  

  
 

    

    
    
吳恩達 改善深層神經網路：超引數除錯、正則化以及優化 第一週
     
  
 
 吳恩達 改善深層神經網路：超引數除錯、正則化以及優化 課程筆記  
 第一週 深度學習裡面的實用層面 
 1.1 測試集/訓練集/開發集 
        原始的機器學習裡面訓練集，測試集和開發集一般按照6:2:2的比例來進行劃分。但是傳統的機器學習 

  
 

    

    
    
deeplearning筆記4：卷積神經網路
     
 
							
							
							卷積神經網路
為什麼要用卷積神經網路-卷積神經網路的作用
防止model overfitting
在計算機視覺中，input vector往往維度很高，將其直接應用於neural network很有可能會造成overfitting，以下圖為例：
在“cat re 

  
 

    

    
    
Coursera-吳恩達-深度學習-神經網路和深度學習-week1-測驗
     
  
 
 本文章內容： 
 Coursera吳恩達深度學習課程，第一課神經網路和深度學習Neural Networks and Deep Learning， 
 第一週：深度學習引言(Introduction to Deep Learning) 
 部分的測驗，題目及答案截圖。 
  
  
 正確:ABC  

  
 

    

    
    
吳恩達學習-深層神經網路
     
 
							
							
							深度學習是指神經網路包含了很多層的隱層，比如說10層20層這樣，有些問題用淺層神經網路不能得到很好的優化，只能通過深層神經網路優化，這是因為深層神經網路有其獨特的優勢，下面我們就先介紹深層神經網路的優勢。

1.深層神經網路的優勢

1.深層神經網路的一大優勢就 

  
 

    

    
    
吳恩達 深度學習 神經網路與深度學習 神經網路基礎 課程作業
     
 
                Part 1：Python Basics with Numpy (optional assignment)

1 - Building basic functions with numpy

Numpy is the main package for scientific c 

  
 

    

    
    
第4門課程-卷積神經網路-第四周作業(影象風格轉換)
     
 
							
							
							0- 背景

所謂的風格轉換是基於一張Content影象和一張Style影象，將兩者融合，生成一張新的影象，分別兼具兩者的內容和風格。 
所需要的依賴如下：



import os
import sys
import scipy.io
import scipy 

  
 

    

    
    
第4門課程-卷積神經網路-第四周作業(人臉識別)
     
 
							
							
							0- 背景

FaceNet從神經網路中學習到以128維度的向量對人臉影象進行表示。通過對比兩個向量的相似度，從而確定兩者是否是同一個人。 
本文中將採用 triplet loss function（三元組的損失函式），且採用一個預訓練的模型對影象進行編碼向量化