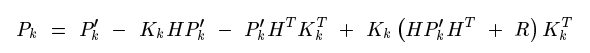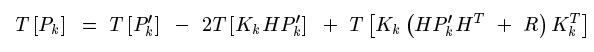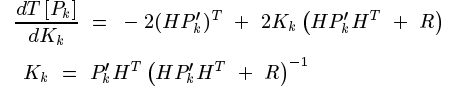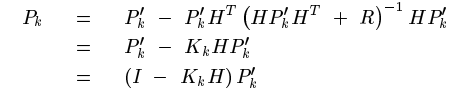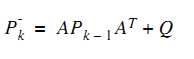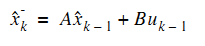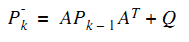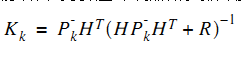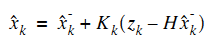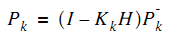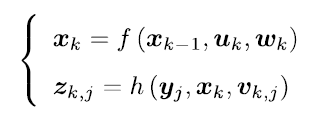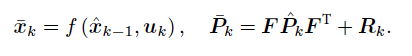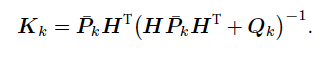隨便寫點關於卡爾曼濾波
看了一篇點選開啟連結部落格,說說我的理解
假設系統此時狀態與上一時刻的狀態有關係(差分方程):
其中,xk為系統現在的狀態變數,xk-1為系統上一時刻的狀態變數,uk-1為系統上一時刻的輸入,wk-1為噪聲。由這個式子可以得到系統狀態的預測值,
觀測方程:
zk為觀測值,xk為系統狀態變數,vk為觀測噪聲。用這個式子和差分方程可以得到觀測值的預測。
很自然地想到用反饋的方式。
重點就是求增益矩陣K。
考慮估計值與真實值的協方差矩陣,由於卡爾曼濾波考慮的誤差是白噪聲,因此協方差矩陣為一個對角線矩陣
把它展開最後得到
使誤差最小,即是使協方差矩陣的跡最小
對其求導,令導數為0,得到K
把K化簡後帶回(這裡沒看懂,高博書上241頁似乎有更靠譜解釋),
式子中還有個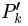
至此,卡爾曼濾波的五條公式就出來了
1計算預測值:
2計算預測值與真實值協方差矩陣
3計算卡爾曼增益係數矩陣
4計算估計值
5計算估計值與真是值之間的協方差矩陣為下一次遞推做準備
這裡面的R與Q分別是狀態方程和觀測方程的噪聲的方差(如何求?)。
考慮到SLAM中的運動方程和觀測方程是
其中xk為機器人位姿,u是感測器讀數(也可以認為是輸入),y為路標,z為觀測資料,w與v是噪聲,顯然,式子中的函式f與h不是一個線性關係,它們無法用矩陣的形式表達出來。對於運動方程,考慮其對xk-1求導後進行泰勒展開。
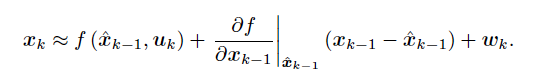
同理,對於觀測方程
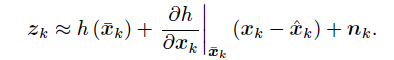
這樣,擴充套件卡爾曼的預測部分和以前類似,但是估計與真實值的協方差矩陣變成了用偏導矩陣來求:
注意,這裡之所以能照搬卡爾曼濾波的公式的形式實際上是因為在卡爾曼濾波中,我們估計值與真實值的誤差表示形式是X-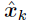
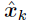
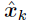
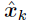
卡爾曼增益矩陣的求法
獲得估計值與下一次預測的預測值與真實值的協方差矩陣