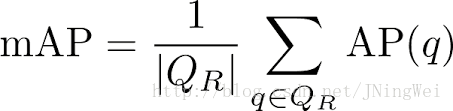準確率(accuracy),精確率(Precision)和召回率(Recall),AP,mAP的概念
先假定一個具體場景作為例子。
假如某個班級有男生80人,女生20人,共計100人.目標是找出所有女生.
某人挑選出50個人,其中20人是女生,另外還錯誤的把30個男生也當作女生挑選出來了.
作為評估者的你需要來評估(evaluation)下他的工作
首先我們可以計算準確率(accuracy),其定義是: 對於給定的測試資料集,分類器正確分類的樣本數與總樣本數之比。也就是損失函式是0-1損失時測試資料集上的準確率.
這樣說聽起來有點抽象,簡單說就是,前面的場景中,實際情況是那個班級有男的和女的兩類,某人(也就是定義中所說的分類器)他又把班級中的人分為男女兩類。accuracy需要得到的是此君分正確的人佔總人數的比例。很容易,我們可以得到:他把其中70(20女+50男)人判定正確了,而總人數是100人,所以它的accuracy就是70 %(70 / 100).
由準確率,我們的確可以在一些場合,從某種意義上得到一個分類器是否有效,但它並不總是能有效的評價一個分類器的工作。舉個例子,google抓取了argcv 100個頁面,而它索引中共有10,000,000個頁面,隨機抽一個頁面,分類下,這是不是argcv的頁面呢?如果以accuracy來判斷我的工作,那我會把所有的頁面都判斷為"不是argcv的頁面",因為我這樣效率非常高(return false,一句話),而accuracy已經到了99.999%(9,999,900/10,000,000),完爆其它很多分類器辛辛苦苦算的值,而我這個演算法顯然不是需求期待的,那怎麼解決呢?這就是precision,recall和f1-measure出場的時間了.
在說precision,recall和f1-measure之前,我們需要先需要定義TP,FN,FP,TN四種分類情況.
按照前面例子,我們需要從一個班級中的人中尋找所有女生,如果把這個任務當成一個分類器的話,那麼女生就是我們需要的,而男生不是,所以我們稱女生為"正類",而男生為"負類".
| 相關(Relevant),正類 | 無關(NonRelevant),負類 | |
| 被檢索到(Retrieved) | true positives(TP 正類判定為正類,例子中就是正確的判定"這位是女生") | false positives(FP 負類判定為正類,"存偽",例子中就是分明是男生卻判斷為女生,當下偽娘橫行,這個錯常有人犯) |
| 未被檢索到(Not Retrieved) | false negatives(FN 正類判定為負類,"去真",例子中就是,分明是女生,這哥們卻判斷為男生--梁山伯同學犯的錯就是這個) | true negatives(TN 負類判定為負類,也就是一個男生被判斷為男生,像我這樣的純爺們一準兒就會在此處) |
通過這張表,我們可以很容易得到例子中這幾個分類的值:TP=20,FP=30,FN=0,TN=50.
精確率”與“召回率”的關係
“精確率”與“召回率”雖然沒有必然的關係(從上面公式中可以看到),然而在大規模資料集合中,這兩個指標卻是相互制約的。
由於“檢索策略”並不完美,希望更多相關的文件被檢索到時,放寬“檢索策略”時,往往也會伴隨出現一些不相關的結果,從而使準確率受到影響。
而希望去除檢索結果中的不相關文件時,務必要將“檢索策略”定的更加嚴格,這樣也會使有一些相關的文件不再能被檢索到,從而使召回率受到影響。
凡是涉及到大規模資料集合的檢索和選取,都涉及到“召回率”和“精確率”這兩個指標。而由於兩個指標相互制約,我們通常也會根據需要為“檢索策略”選擇一個合適的度,不能太嚴格也不能太鬆,尋求在召回率和精確率中間的一個平衡點。這個平衡點由具體需求決定。
===================================
mAP 概念
P
precision,即 準確率 。
R
recall,即 召回率 。
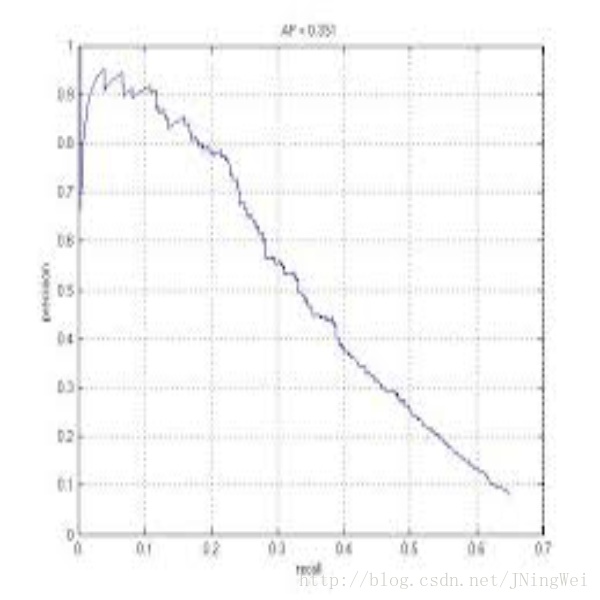
PR曲線
即 以 precision 和 recall 作為 橫縱軸座標 的二維曲線。
一般來說,precision 和 recall 是 魚與熊掌 的關係。下圖即是 PR曲線:
AP值
Average Precision,即 平均精確度 。
如何衡量一個模型的效能,單純用 precision 和 recall 都不科學。於是人們想到,哎嘛為何不把 PR曲線下的面積 當做衡量尺度呢?於是就有了 AP值 這一概念。這裡的 average,等於是對 precision 進行 取平均 。
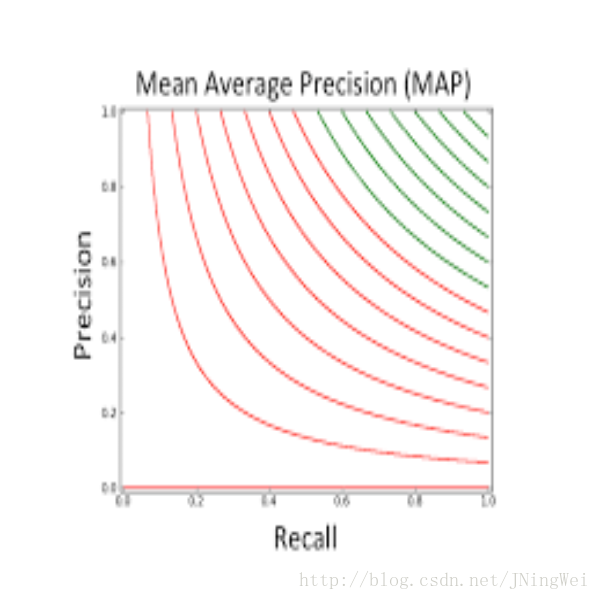
mAP值
Mean Average Precision,即 平均AP值 。
是對多個驗證集個體 求 平均AP值 。如下圖:
mAP 計算
公式
Code
def compute_ap(gt_boxes, gt_class_ids,
pred_boxes, pred_class_ids, pred_scores,
iou_threshold=0.5):
"""Compute Average Precision at a set IoU threshold (default 0.5).
Returns:
mAP: Mean Average Precision
precisions: List of precisions at different class score thresholds.
recalls: List of recall values at different class score thresholds.
overlaps: [pred_boxes, gt_boxes] IoU overlaps.
"""
# Trim zero padding and sort predictions by score from high to low
gt_boxes = trim_zeros(gt_boxes)
pred_boxes = trim_zeros(pred_boxes)
pred_scores = pred_scores[:pred_boxes.shape[0]]
indices = np.argsort(pred_scores)[::-1]
pred_boxes = pred_boxes[indices]
pred_class_ids = pred_class_ids[indices]
pred_scores = pred_scores[indices]
# Compute IoU overlaps [pred_boxes, gt_boxes]
overlaps = compute_overlaps(pred_boxes, gt_boxes)
# Loop through ground truth boxes and find matching predictions
match_count = 0
pred_match = np.zeros([pred_boxes.shape[0]])
gt_match = np.zeros([gt_boxes.shape[0]])
for i in range(len(pred_boxes)):
# Find best matching ground truth box
sorted_ixs = np.argsort(overlaps[i])[::-1]
for j in sorted_ixs:
# If ground truth box is already matched, go to next one
if gt_match[j] == 1:
continue
# If we reach IoU smaller than the threshold, end the loop
iou = overlaps[i, j]
if iou < iou_threshold:
break
# Do we have a match?
if pred_class_ids[i] == gt_class_ids[j]:
match_count += 1
gt_match[j] = 1
pred_match[i] = 1
break
# Compute precision and recall at each prediction box step
precisions = np.cumsum(pred_match) / (np.arange(len(pred_match)) + 1)
recalls = np.cumsum(pred_match).astype(np.float32) / len(gt_match)
# Pad with start and end values to simplify the math
precisions = np.concatenate([[0], precisions, [0]])
recalls = np.concatenate([[0], recalls, [1]])
# Ensure precision values decrease but don't increase. This way, the
# precision value at each recall threshold is the maximum it can be
# for all following recall thresholds, as specified by the VOC paper.
for i in range(len(precisions) - 2, -1, -1):
precisions[i] = np.maximum(precisions[i], precisions[i + 1])
# Compute mean AP over recall range
indices = np.where(recalls[:-1] != recalls[1:])[0] + 1
mAP = np.sum((recalls[indices] - recalls[indices - 1]) *
precisions[indices])
return mAP, precisions, recalls, overlaps