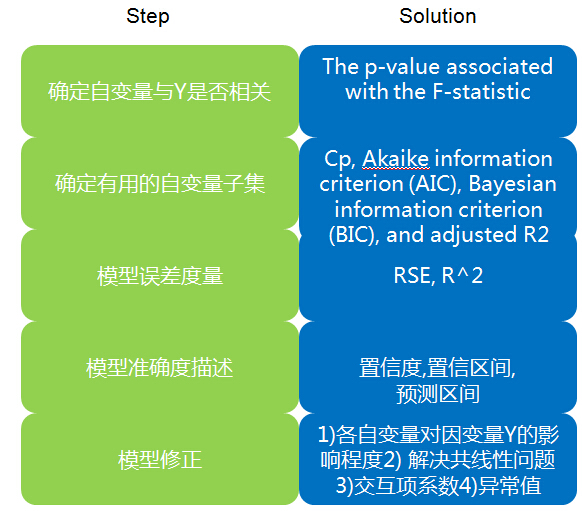
1. 確定自變數與Y是否相關

證明：自變數X1，X2，....XP中至少存在一個自變數與因變數Y相關 For any given value of n（觀測資料的數目） and p（自變數X的數目）, any statistical software  package can be used to compute the p-value associated with the F-statistic using this distribution. Based on this p-value, we can determine whether or not to reject H0. （用軟體計算出的與F-statistic 相關的p-value來驗證假設，the p-value associated with the F-statistic

） 例子： Is there a relationship between advertising sales（銷售額） and budget（廣告預算：TV, radio, and newspaper）? the p-value corresponding to the F-statistic in Table 3.6 is very low, indicating clear evidence of a relationship between advertising and sales.

背景知識回顧：

t-statistic T統計量（t檢驗）與F-statistic
t-statistic T統計量=（迴歸係數β的估計值-0）/β的標準誤 ，which measures the number of standard deviations thatβis away from 0。用來對計量經濟學模型中關於引數的單個假設進行檢驗的一種統計量。  我們一般用t統計量來檢驗迴歸係數是否為0做檢驗。例如：線性迴歸Y=β0+β1X，為了驗證X與Y是否相關，  假設H0：X與Y無關,即β1=0 假設H1：X與Y相關,即β1不等於0 計算t-statistic， 如果t-statistic is far away from zero,則x和y相關。一般用p-values來檢驗X和Y是否相關。

1）p-values（Probability，Pr） 1 定義 pvalue的定義：在原假設正確的情況下，出現當前情況或者更加極端情況的概率。 p值是用來衡量統計顯著性的常用指標。 P值( P-Value，Probability，Pr）即概率，反映某一事件發生的可能性大小。統計學根據顯著性檢驗方法所得到的P 值，一般以P < 0.05 為顯著， P <0.01 為非常顯著，其含義是樣本間的差異由抽樣誤差所致的概率小於0.05 或0.01。實際上，P 值不能賦予資料任何重要性，只能說明某事件發生的機率。 假設檢驗是推斷統計中的一項重要內容。在假設檢驗中常見到P 值( P-Value，Probability，Pr)，P 值是進行檢驗決策的另一個依據。 大的pvalue說明還沒有足夠的證據拒絕原假設。 2 為何有p-value P值方法的思路是先進行一項實驗，然後觀察實驗結果是否符合隨機結果的特徵。研究人員首先提出一個他們想要推翻的“零假設”（null hypothesis），比如，兩組資料沒有相關性或兩組資料沒有顯著差別。接下來，他們會故意唱反調，假設零假設是成立的，然後計算實際觀察結果與零假設相吻合的概率。這個概率就是P值。費希爾說，P值越小，研究人員成功證明這個零假設不成立的可能性就越大。 其實理解起來很簡單，基本原理只有兩個： 1）一個命題只能證偽，不能證明為真 2）小概率事件不可能發生 證明邏輯就是：我要證明命題為真->證明該命題的否命題為假->在否命題的假設下，觀察到小概率事件發生了->搞定。 3 demo 投飛鏢，假設一個飛鏢有10，9,8,7,6,5,4,3,2,1總共十個環（10是中心），定義合格投手為其真實水平能投到10~3環，而不管他臨場表現如何。假設10~3環佔靶子面積的95%。 H0：A是一個合格投手 H1：A不是合格投手 結合這個例子來看：證明A是合格的投手-》證明“A不是合格投手”的命題為假-》觀察到一個事件（比如A連續10次投中10環），而這個事件在“A不是合格投手”的假設下，概率為p，小於0.05->小概率事件發生，否命題被推翻。 可以看到p越小-》這個事件越是小概率事件-》否命題越可能被推翻-》原命題越可信
2）F-statistic t檢驗是單個係數顯著性的檢驗，檢驗一個變數X與Y是否相關，如電視上廣告投入是否有利於銷售額。T檢驗的原假設為某一解釋變數的係數為0 。 F檢驗是是所有的自變數在一起對因變數的影響，當處理3個及其以上的時候（變數X1，X2，X3...等）用的是F檢驗。F檢驗的原假設為所有迴歸係數為0。 即F檢驗用於證明變數X1，X2，X3...中至少有一個變數和Y相關
F檢驗的原假設是H0：所有迴歸引數都等於0，所以F檢驗通過的話說明模型總體存在，F檢驗不通過，其他的檢驗就別做了，因為模型所有引數不顯著異於0，相當於模型不存在（即沒有任何一個變數X1，X2，X3... have no relationship with Y）。

2.確定有用的自變數子集

Do all the predictors help to explain Y , or is only a subset of the  predictors useful? （確定對Y有用的自變數） The first step in a multiple regression analysis is to compute the F-statistic and to examine the associated pvalue. If we conclude on the basis of that p-value that at least one of the predictors is related to the response, then it is natural to wonder which are the guilty ones!

The task of determining which predictors are associated with the response, in order to fit a single model involving only those predictors, is referred to as variable selection.

There are three classical approaches for this task:Forward selection.Forward selection.Forward selection. 1）Forward selection.  We begin with the null model—a model that conforward  selection null model tains an intercept but no predictors. We then fit p simple linear regressions  and add to the null model the variable that results in the  lowest RSS. We then add to that model the variable that results in the lowest RSS for the new two-variable model. This approach is  continued until some stopping rule is satisfied. 2)Backward selection.  We start with all variables in the model, and  backward remove the variable with the largest p-value—that is, the variable selection that is the least statistically significant. The new (p − 1)-variable model is fit, and the variable with the largest p-value is removed. This procedure continues until a stopping rule is reached. For instance, we may stop when all remaining variables have a p-value below some threshold. 3)Mixed selection.  This is a combination of forward and backward semixed  lection. We start with no variables in the model, and as with forward selection , we add the variable that provides the best fit. We continue to add variables one-by-one. Of course, as we noted with the Advertising example, the p-values for variables can become larger as new predictors are added to the model. Hence, if at any point the p-value for one of the variables in the model rises above a certain threshold, then we remove that variable from the model. We continue to perform these forward and backward steps until all variables in the model have a sufficiently low p-value, and all variables outside the model would have a large p-value if added to the model. Compare: Backward selection requires that the number of samples n is larger than  the number of variables p (so that the full model can be fit). In contrast, forward stepwise can be used even when n < p, and so is the only viable subset method when p is very large. How to  selecting the best model among a collection of models with different numbers of predictors? Instead, we wish to choose a model with a low test error. As is evident here, the training error can be a poor estimate of the test error. Therefore, RSS and R2 are not suitable for selecting the best model among a collection of models with different numbers of predictors. These approaches can be used to select among a set of models with different numbers of variables. Cp, Akaike information criterion (AIC), Bayesian information criterion (BIC), and adjusted R2 In the past, performing cross-validation was computationally prohibitive  for many problems with large p and/or large n, and so AIC, BIC, Cp, and adjusted R2 were more attractive approaches for choosing among a set of models. However, nowadays with fast computers, the computations required to perform cross-validation are hardly ever an issue. Thus, crossvalidation is a very attractive approach for selecting from among a number of models under consideration. TODO chapter6 <Linear Model Selection and Regularization>

3.模型誤差（RSE,R^2）

How well does the model fit the data? An R2 value close to 1 indicates that the model explains a large portion of the variance（自變數X） in the response variable（因變數Y）. 
It turns out that R2 will always increase when more variables are added to the model, even if those variables are only weakly associated with the response.
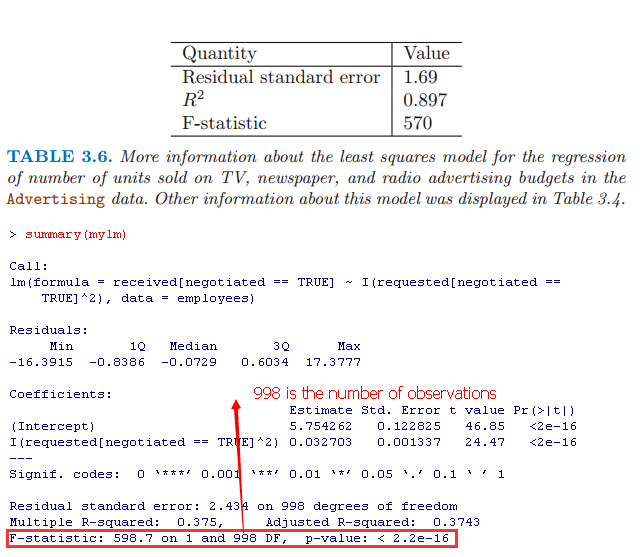
例子： For the Advertising data, the RSE is 1,681units while the mean value for the response is 14,022, indicating a percentage error of roughly 12 %(RSE/mean value). Second, the R2 statistic records the percentage of variability in the response that is explained by the predictors. The predictors explain almost 90 % of the variance in sales. 

背景知識： RSE標準差
R2 Statistic（R-square）用於評判一個模型擬合好壞的重要標準 R平方介於0~1之間，越接近1，迴歸擬合效果越好，模型越精確。
R^2判定係數就是擬合優度判定係數，它體現了迴歸模型中自變數Y的變異在因變數X的變異中所佔的比例。即用來表示y值中有多少可以用x值來解釋（R2 measures the proportion
of variability in Y that can be explained using X.），0.92的意思就是y值中有92%可以用x值來解釋。 當R^2=1時表示，所有觀測點都落在擬合的直線或曲線上；當R^2=0時，表示自變數與因變數不存在直線或曲線關係。 如何根據R-squared判斷模型是否準確？ However, it can  still be challenging to determine what is a good R2 value, and in general,  this will depend on the application. For instance, in certain problems in  physics, we may know that the data truly comes from a linear model with  a small residual error. In this case, we would expect to see an R2 value that is extremely close to 1, and a substantially smaller R2 value might indicate a serious problem with the experiment in which the data were generated. On the other hand, in typical applications in biology, psychology, marketing, and other domains, the linear model (3.5) is at best an extremely rough approximation to the data, and residual errors due to other unmeasured factors are often very large. In this setting, we would expect only a very small proportion of the variance in the response to be explained by the  predictor, and an R2 value well below 0.1 might be more realistic!

4.應用模型：Y準確度（置信度，置信區間，預測區間）

Given a set of predictor values, what response value should we predict, and how accurate is our prediction? Once we have fit the multiple regression model, it is straightforward to apply  in order to predict the response Y on the basis of a set of values for the predictors X1, X2, . . . , Xp. 

We can compute a confidence interval （置信區間）in order to determine how close Y'(用模型計算出的值) will be to f(X)（理論中的真實值）. predict an individual response use prediction interval, predict the average response use confidence interval.
confidence interval置信區間 與預測區間 1 置信區間 表示在給定預測變數的指定設定時，平均響應可能落入的範圍。 
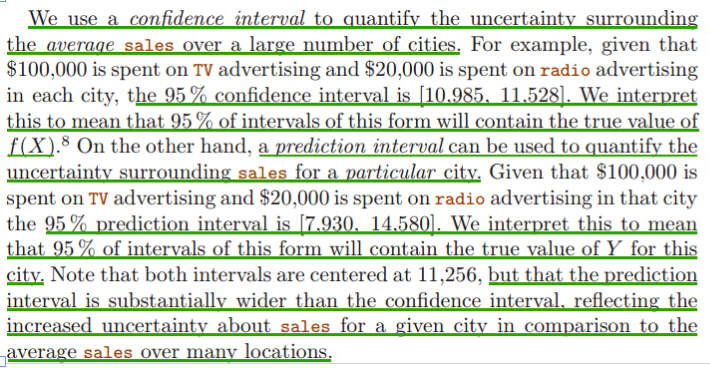
置信區間是結合置信度來說的，簡單來說就是隨機變數有一定概率落在一個範圍內，這個概率就叫置信度，範圍就是對應的置信區間。 真實資料往往是實際上不能獲知的，我們只能進行估計，估計的結果是給出一對資料，比如從1到1.5，真實的值落在1到1.5之間的可能性是95%（也有5%的可能性在這區間之外的）。 90%置信區間（Confidence Interval,CI）：當給出某個估計值的90%置信區間為【a,b】時，可以理解為我們有90%的信心（Confidence）可以說樣本的平均值介於a到b之間，而發生錯誤的概率為10%。  2 預測區間Prediction Interval 表示在給定預測變數的指定設定時，單個觀測值可能落入的範圍。
預測區間PI總是要比對應的置信區間CI大，這是因為在對單個響應與響應均值的預測中包括了更多的不確定性。
The basic syntax is lm(y∼x,data), where y is the response（預測值）, x is the predictor（影響因子：x1,x2）, and data is the data set in which these two variables are kept.

5.模型修正

1）各自變數X1，X2...對因變數Y的影響 程度

Which media contribute to sales? To answer this question, we can examine the p-values associated with  each predictor’s t-statistic. In the multiple linear regression displayed in Table 3.4, the p-values for TV and radio are low,but the p-value for newspaper is not. This suggests that only TV and radio are related to sales. 

2）解決共線性問題

所謂多重共線性（Multicollinearity）是指線性迴歸模型中的解釋變數之間由於存在精確相關關係或高度相關關係而使模型估計失真或難以估計準確。一般來說，由於經濟資料的限制使得模型設計不當，導致設計矩陣中解釋變數間存在普遍的相關關係。
如何解決共線性問題？ 方差膨脹因子（Variance Inflation Factor，VIF）：容忍度的倒數，VIF越大，顯示共線性越嚴重。經驗判斷方法表明：當0＜VIF＜10，不存在多重共線性；當10≤VIF＜100，存在較強的多重共線性；當VIF≥100，存在嚴重多重共線性。

3）互動項係數（interaction terms）

衡量的是一個變數對於“另一個變數對因變數影響能力”的影響。 Is there synergy among the advertising media? Perhaps spending $50,000 on television advertising and $50,000 on  radio advertising results in more sales than allocating $100,000 to either television or radio individually. In marketing, this is known as  a synergy effect, while in statistics it is called an interaction effect. 何時適合在模型中加入互動係數？

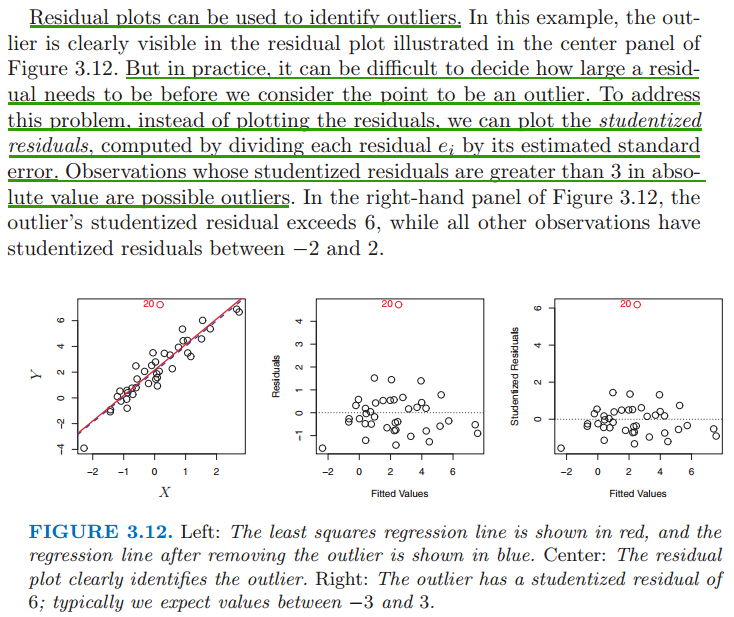
4）異常值outlier檢測

Residual plots（殘差散點圖） can be used to identify outliers. 檢測到異常值後，從資料中去掉異常值，再生成糾正後的模型。
殘差是指觀測值與預測值（擬合值）之間的差，即是實際觀察值與迴歸估計值的差。 殘差分析就是通過殘差所提供的資訊，分析出資料的可靠性、週期性或其它干擾。線上性迴歸中,殘差的重要應用之一是根據它的絕對值大小判定異常點。 But in practice, it can be difficult to decide how large a residual needs to be before we consider the point to be an outlier. To address this problem, instead of plotting the residuals, we can plot the studentized residuals, computed by dividing each residual ei by its estimated standard studentized error. Observations whose studentized residuals are greater than 3 in abso- residuallute value are possible outliers.