【雜紀】從ROC曲線到AUC值,再到Mann–Whitney U統計量
統計檢驗中的兩類錯誤
在進行假設檢驗時,分別提出原假設(Null Hypothesis)和備擇假設(Alternative Hypothesis),檢驗結果可能出現的兩類錯誤:
- 原假設實際上是正確的,而檢驗結果卻拒絕原假設,稱為
第一類/第一型錯誤(Type I error)、棄真錯誤 - 原假設實際上是錯誤的,而檢驗結果卻接受原假設,稱為
第二類/第二型錯誤(Type II error)、取偽錯誤
ROC Curve
起源與發展
ROC曲線(Receiver Operating Characteristic Curve),又稱為感受性曲線(Sensitivity Curve),是一種座標圖式的分析工具。它首先是由二戰中的電子工程師和雷達工程師發明的,用來偵測戰場上的敵軍載具(飛機、船艦),即訊號檢測理論。之後很快就被引入了心理學來進行訊號的知覺檢測。數十年來,ROC分析被用於醫學、無線電、生物學、犯罪心理學領域中,最近在機器學習和資料探勘領域也得到了很好的發展。用途
ROC曲線用於衡量
二元分類模型的優劣,也就是說,它所衡量的模型,一定只有兩個判斷結果(非黑即白):陽性/陰性、得病/不得病、違約/不違約、敵軍/非敵軍、正例/負例…等,通常將這兩種結果分別記為1和0。例如,有一個模型,可以用來判斷人體是否得病。現將五個身體狀況分別為
健康(0)、得病(1)、健康(0)、健康(0)、得病(1)的樣本的各項生理指標輸入該模型,並假設模型輸出的五個人的得病概率分別為0.30,0.60,0.55,0.40,0.50。注意,在做ROC曲線分析時,輸入模型的待判別樣本全部是已知真值的,如上例的樣本,已知其是健康、得病、健康、健康、得病。那麼,得到這五個概率後,模型又是怎樣進一步判別他們是否得病的?首先拋開我們傳統的
0.50認知,這裡並不是概率大於0.50就認為該樣本得病了。因為模型準確性本身就是待驗證的,其得到的預測結果當然也不是百分之百正確,這時候就需要醫生結合從業經驗,人為給定一個閾值(threshold),也稱為cut-off point。只有當樣本的預測概率大於閾值時,才將該樣本歸為得病。顯然,如果閾值過低(判為得病的條件寬鬆,得病門檻低),就容易將健康樣本誤判為得病;如果閾值過高(判為得病的條件嚴謹,得病門檻高),就容易漏掉真正的得病樣本,使一部分得病樣本誤判為健康。為了幫助理解,我們將分類模型視為一個篩網,閾值高低視為篩網孔的尺寸,
健康樣本為大沙粒,得病樣本為小沙粒,則通過篩網的,應該是得病樣本;而留在篩網上的,應該是健康樣本。那麼:- 閾值過低 = 判為得病的條件寬鬆 = 篩網孔過大 = 大沙粒(健康樣本)也不小心通過篩網(誤判為得病)
- 閾值過高 = 判為得病的條件嚴謹 = 篩網孔過小 = 小沙粒(得病樣本)過不去,滯留在篩網(誤判為健康)
由此可見,只有選定閾值以後,才能把模型預測概率轉化為具體的類別,而不同的閾值對模型的判別效果有很大的影響。閾值雖然不能窮舉(其取值從0-1),但取不同的閾值,對模型分類結果的影響卻是可以羅列出來的。結合上面的例子,可以設定如下6個範圍的閾值,並得到如下6種不同的分類結果。可以看到,閾值過低時,模型將所有樣本都判為得病;閾值過高時,模型將所有樣本都判為健康:
| 閾值t的範圍 | 預測結果 |
|---|---|
| 0 t 0.30 | (得病,得病,得病,得病,得病)記為(1,1,1,1,1) |
| 0.30 t 0.40 | (健康,得病,得病,得病,得病)記為(0,1,1,1,1) |
| 0.40 t 0.50 | (健康,得病,得病,健康,得病)記為(0,1,1,0,1) |
| 0.50 t 0.55 | (健康,得病,得病,健康,健康)記為(0,1,1,0,0) |
| 0.55 t 0.60 | (健康,得病,健康,健康,健康)記為(0,1,0,0,0) |
| t 0.60 | (健康,健康,健康,健康,健康)記為(0,0,0,0,0) |
定義
以上通過例項,對ROC曲線所衡量的模型進行了簡單解釋。回到ROC曲線本身,既然是呈現在座標圖上的曲線,則一定有橫、縱座標兩個變數。而且ROC曲線是衡量模型優劣,必然要對模型的分類結果進行統計分析,因此RCO曲線分析的基礎,就是上述表格中的資料。
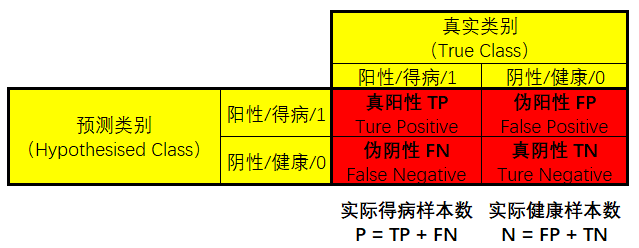
顯然,6個分類結果對比真實情況,各有差異。這時候,我們最想了解的應該是:該模型判別的正確率有多高?事實上,判斷結果一定是如下情況之一:- 得病樣本被正確判斷為得病樣本(
真陽性TP) - 得病樣本被誤判為健康樣本(
偽陰性FN) - 健康樣本被正確判斷為健康樣本(
真陰性TN) - 健康樣本被誤判為得病樣本(
偽陽性FP)
在醫學統計中,假設檢驗的原假設是樣本健康,備擇假設是樣本得病。那麼,
偽陽性FP的情況是:明明健康,卻判其得病,是對得病的錯誤肯定,拒絕了正確的原假設,屬於棄真錯誤。
而偽陰性FN的情況是:明明得病,卻判其健康,是對得病的錯誤否定,接受了錯誤的原假設,屬於取偽錯誤。
從而可以引入一系列常見的效能指標:TPR(True Positive Rate)= = ,稱為真陽性率
又可稱命中率(Hit Rate)、敏感度(Sensitivity)FPR(False Positive Rate)= = ,稱為偽陽性率
又可稱錯誤命中率/假警報率(False Alarm Rate)TNR(True Negative Rate)= = = ,稱為真陰性率
又可稱特異度(Specificity)Recall=TPR= = ,稱為召回率Precision= ,稱為精確率ACC(Accuracy)= ,稱為準確度F-measure= = ,稱為F1值/F1評分
所以,ROC曲線是以
FPR為橫座標、以TPR為縱座標所形成的曲線,其座標點為(FPR,TPR)。注意,工程上一般不採用FPR、TPR這兩個術語,而是分別用1-Specificity、Sensitivity來代替,則ROC曲線上的座標點為(1-Specificity,Sensitivity)。依舊沿用上述例子,模型根據不同的閾值,每得到一個預測結果,就可以與真值(0,1,0,0,1)做一次對比,並計算出一個座標點(FPR,TPR)。因此,上述例子的ROC曲線有6個座標點,手動計算並用R語言作圖驗證如下:- 得病樣本被正確判斷為得病樣本(
| 閾值t的範圍 | 預測結果 | 指標值 | (FPR,TPR) |
|---|---|---|---|
| 0 t 0.30 | (1,1,1,1,1) | FP = 3,TN = 0,TP = 2,FN = 0 | (1,1) |
| 0.30 t 0.40 | (0,1,1,1,1) | FP = 2,TN = 1,TP = 2,FN = 0 | (,1) |
| 0.40 t 0.50 | (0,1,1,0,1) | FP = 1,TN = 2,TP = 2,FN = 0 | (,1) |
| 0.50 t 0.55 | (0,1,1,0,0) | FP = 1,TN = 2,TP = 1,FN = 1 | (,) |
| 0.55 t 0.60 | (0,1,0,0,0) | FP = 0,TN = 3,TP = 1,FN = 1 | (0, |