1.為什麼我們要用roc曲線進行評價

用傳統的識別率來評價模型的話會有下面的缺陷：

在類不平衡的情況下,
如正樣本90個,負樣本10個,直接把所有樣本分類為正樣本,得到識別率為90%
而如果正樣本識別對75個，負樣本識別對5個，得到的識別率為80%。
但是這樣的識別率評價指標導致高分模型不具有魯棒性(即該模型在類別平衡下表現不好)
所以我們要換一種評價指標就有了roc曲線

2.那麼roc曲線到底是什麼呢？

對於一個二分類問題，我們有如下圖4種情況
i. 預測為正，真實為正(預測正確)即下圖的:TP
ii.預測為正，真實為反(預測錯誤)即下圖的:FP
iii.預測為反，真實為正(預測正確)即下圖的:FN
iv.預測為反，真實為反(預測錯誤)即下圖的:TN

TPR（靈敏度)=正樣本預測正確結果數 / 正樣本實際數
TPR=TP/(TP+FN)

FPR(特製度)=被預測為正的負樣本結果數 /負樣本實際數
FPR=FP/(FP+TN)

以FPR為橫軸，TPR為負軸作圖就有了roc曲線

我們從幾個特殊點看是怎麼反應指標的
第一個點，(0,1)
即FPR=0, TPR=1，這意味著FN（false negative）=0，並且FP（false positive）=0。Wow，這是一個完美的分類器，它將所有的樣本都正確分類。

第二個點，(1,0)
即FPR=1，TPR=0，類似地分析可以發現這是一個最糟糕的分類器，因為它成功避開了所有的正確答案。

第三個點，(0,0)
即FPR=TPR=0，即FP（false positive）=TP（true positive）=0，可以發現該分類器預測所有的樣本都為負樣本（negative）。

第四個點（1,1）
分類器實際上預測所有的樣本都為正樣本。

綜上所述
我們可以斷言，ROC曲線越接近左上角，該分類器的效能越好，也就防止了類別不平衡導致的錯誤評分

3.那麼我們怎麼畫roc曲線呢？

這裡我借用大多數部落格的內容來說
“Class”一欄表示每個測試樣本真正的標籤（p表示正樣本，n表示負樣本），“Score”表示每個測試樣本屬於正樣本的概率

接下來，我們從高到低，依次將“Score”值作為閾值threshold，當測試樣本屬於正樣本的概率大於或等於這個threshold時，我們認為它為正樣本，否則為負樣本。舉例來說，對於圖中的第4個樣本，其“Score”值為0.6，那麼樣本1，2，3，4都被認為是正樣本，因為它們的“Score”值都大於等於0.6，而其他樣本則都認為是負樣本。每次選取一個不同的threshold，我們就可以得到一組FPR和TPR，即ROC曲線上的一點。這樣一來，我們一共得到了20組FPR和TPR的值，將它們畫在ROC曲線的結果如下圖：

4.roc曲線和auc什麼關係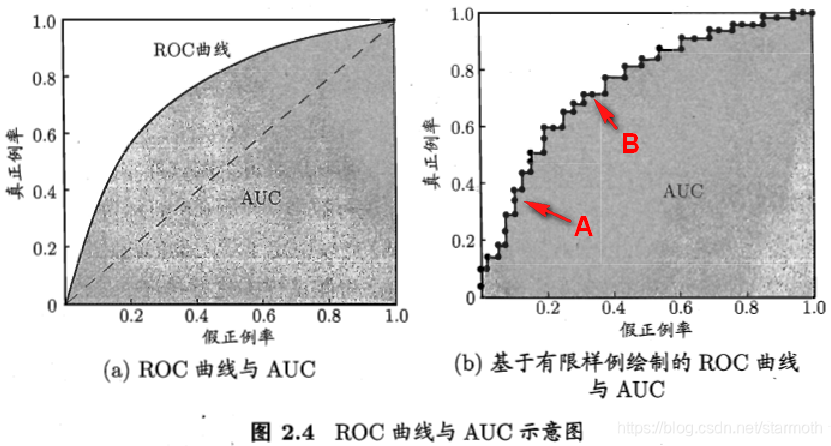

這兩個圖很清晰得表面了兩種關係：
即auc為roc曲線以下的部分

5.auc表示了什麼？

AUC（Area Under Curve）被定義為ROC曲線下的面積，顯然這個面積的數值不會大於1。又由於ROC曲線一般都處於y=x這條直線的上方，所以AUC的取值範圍在0.5和1之間。使用AUC值作為評價標準是因為很多時候ROC曲線並不能清晰的說明哪個分類器的效果更好，而作為一個數值，對應AUC更大的分類器效果更好。

AUC = 1，是完美分類器，採用這個預測模型時，不管設定什麼閾值都能得出完美預測。絕大多數預測的場合，不存在完美分類器。
0.5 < AUC < 1，優於隨機猜測。這個分類器（模型）妥善設定閾值的話，能有預測價值。
AUC = 0.5，跟隨機猜測一樣（例：丟銅板），模型沒有預測價值。
AUC < 0.5，比隨機猜測還差；但只要總是反預測而行，就優於隨機猜測，因此不存在AUC < 0.5的情況。

綜上auc的值往往反應了模型的分類效果好不好魯棒性強不強。是個非常適用的指標