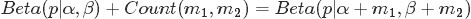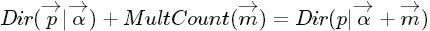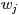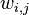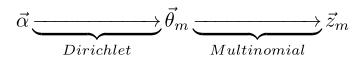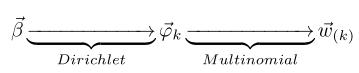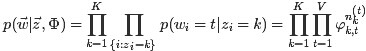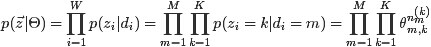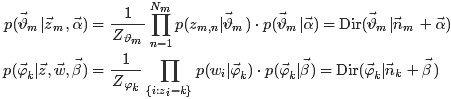主題模型TopicModel:隱含狄利克雷分佈LDA
主題模型LDA簡介
隱含狄利克雷分佈簡稱LDA(Latent Dirichlet allocation),首先由Blei, David M.、吳恩達和Jordan, Michael I於2003年提出,目前在文字挖掘領域包括文字主題識別、文字分類以及文字相似度計算方面都有應用。
LDA是一種典型的詞袋模型,即它認為一篇文件是由一組詞構成的一個集合,詞與詞之間沒有順序以及先後的關係。一篇文件可以包含多個主題,文件中每一個詞都由其中的一個主題生成。
它是一種主題模型,它可以將文件集中每篇文件的主題按照概率分佈的形式給出;
同時是一種無監督學習演算法,在訓練時不需要手工標註的訓練集,需要的僅僅是文件集以及指定主題的數量k即可;
此外LDA的另一個優點則是,對於每一個主題均可找出一些詞語來描述它;
LDA可以被認為是一種聚類演算法:
- 主題對應聚類中心,文件對應資料集中的例子。
- 主題和文件在特徵空間中都存在,且特徵向量是詞頻向量。
- LDA不是用傳統的距離來衡量一個類簇,它使用的是基於文字文件生成的統計模型的函式。
LDA的概率圖及生成表示

Note:
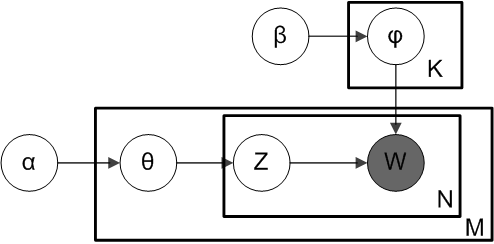
1 陰影圓圈表示可觀測的變數,非陰影圓圈表示隱變數;箭頭表示兩變數間的條件依賴性;方框表示重複抽樣,方框右下角的數字代表重複抽樣的次數。這種表示方法也叫做plate notation,參考PRML 8.0 Graphical Models。
對應到圖2, α⃗ 和 β⃗ 是超引數;方框中, Φ={φ⃗ k} 表示有 K 種“主題-詞項”分佈; Θ={ϑ⃗ m} 有 M 種“文件-主題”分佈,即對每篇文件都會產生一個 ϑ⃗ m 分佈;每篇文件 m 中有 n 個詞,每個詞 wm,n 都有一個主題 zm,n ,該詞實際是由 φ⃗ zm,n 產生。
2 β⃗ 到φ(生成topic-word分佈的分佈) and α⃗到θ(生成doc-topic分佈的分佈) 是狄利克雷分佈,θ生成z(賦給詞w的主題) and φ生成w(當前詞) 是多項式分佈。θ指向z是從doc-topic分佈中取樣一個主題賦給w(但是此時還不知道詞w具體是什麼,而是隻知道其主題),φ指向w是φ的topic-word分佈依賴於w。
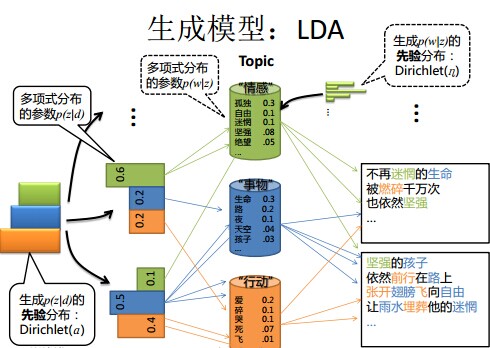
LDA生成模型
當我們看到一篇文章後,往往喜歡推測這篇文章是如何生成的,我們可能會認為作者先確定這篇文章的幾個主題,然後圍繞這幾個主題遣詞造句,表達成文。LDA就是要根據給定的一篇文件,推測其主題分佈。
因此正如LDA貝葉斯網路結構中所描述的,在LDA模型中一篇文件生成的方式如下:
- 從狄利克雷分佈
 中取樣生成文件i的主題分佈
中取樣生成文件i的主題分佈
- 從主題的多項式分佈
 中取樣生成文件i第j個詞的主題
中取樣生成文件i第j個詞的主題
- 從狄利克雷分佈
 中取樣生成主題
中取樣生成主題 的詞語分佈
的詞語分佈
- 從詞語的多項式分佈
 中取樣最終生成詞語
中取樣最終生成詞語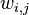
LDA模型引數求解概述
因此整個模型中所有可見變數以及隱藏變數的聯合分佈是
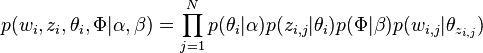 (這裡i表示第i個文件)
(這裡i表示第i個文件)
最終一篇文件的單詞分佈的最大似然估計可以通過將上式的 以及
以及 進行積分和對
進行積分和對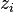 進行求和得到
進行求和得到
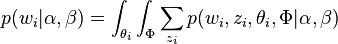
根據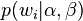 的最大似然估計,最終可以通過吉布斯取樣等方法估計出模型中的引數。
的最大似然估計,最終可以通過吉布斯取樣等方法估計出模型中的引數。
LDA的引數估計(吉布斯取樣)
在LDA最初提出的時候,人們使用EM演算法進行求解。
後來人們普遍開始使用較為簡單的Gibbs Sampling,具體過程如下:
- 首先對所有文件中的所有詞遍歷一遍,為其都隨機分配一個主題,即zm,n=k~Mult(1/K),其中m表示第m篇文件,n表示文件中的第n個詞,k表示主題,K表示主題的總數,之後將對應的n(k)m+1, nm+1, n(t)k+1, nk+1, 他們分別表示在m文件中k主題出現的次數,m文件中主題數量的和??(可重複的,所以應該就是文件中詞的個數,不變的量)??,k主題對應的t詞的次數,k主題對應的總詞數(n(k)m等等初始化為0)。
- 之後對下述操作進行重複迭代。
- 對所有文件中的所有詞進行遍歷,假如當前文件m的詞t對應主題為k,則n(k)m-1, nm-1, n(t)k-1, nk-1, 即先拿出當前詞,之後根據LDA中topic sample的概率分佈取樣出新主題,在對應的n(k)m, nm, n(t)k, nk上分別+1。
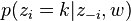 ∝
∝ 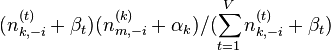 (topic sample的概率分佈)
(topic sample的概率分佈)
- 迭代完成後輸出主題-詞引數矩陣φ和文件-主題矩陣θ
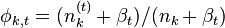 主題k中詞t的概率分佈
主題k中詞t的概率分佈
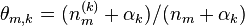 文件m中主題k的概率分佈
文件m中主題k的概率分佈
從這裡看出,gibbs取樣方法求解lda最重要的是條件概率p(zi | z-i,w)的計算上。
LDA中的數學基礎
- beta分佈是二項式分佈的共軛先驗概率分佈:“對於非負實數
和
,我們有如下關係
其中
對應的是二項分佈
的計數。針對於這種觀測到的資料符合二項分佈,引數的先驗分佈和後驗分佈都是Beta分佈的情況,就是Beta-Binomial 共軛。”
- 狄利克雷分佈(Dirichlet分佈)是多項式分佈的共軛先驗概率分佈:
- “ 把
從整數集合延拓到實數集合,從而得到更一般的表示式如下:
- “ 把
針對於這種觀測到的資料符合多項分佈,引數的先驗分佈和後驗分佈都是Dirichlet 分佈的情況,就是 Dirichlet-Multinomial 共軛。 ”
正如Beta分佈是二項式分佈的共軛先驗概率分佈,狄利克雷分佈作為多項式分佈的共軛先驗概率分佈。
- 貝葉斯派思考問題的固定模式:
- 先驗分佈
+ 樣本資訊
後驗分佈
的認知是先驗分佈
,在得到新的樣本資訊
後,人們對
的認知為
。
- 先驗分佈
- 頻率派與貝葉斯派各自不同的思考方式:
- 頻率派把需要推斷的引數θ看做是固定的未知常數,即概率
雖然未知,但是是確定的一個值,同時樣本X 是隨機的,所以頻率派重點研究樣本空間,大部分的概率計算都是針對樣本X 的分佈;
- 而貝葉斯派的觀點則截然相反,他們認為待估計的引數
是隨機變數,服從一定的分佈,而樣本X 是固定的,由於樣本是固定的,所以他們重點研究的是引數
的分佈。
- 頻率派把需要推斷的引數θ看做是固定的未知常數,即概率
主題模型LDA文件生成模式
理解lda生成詞的關鍵,lz建議先看lda基礎模型。當然,已經理解可以直接跳過,看推理引數部分。
從LDA與pLSA的區別和聯絡角度出發
LDA就是在pLSA的基礎上加層貝葉斯框架。pLSA樣本隨機,引數雖未知但固定,屬於頻率派思想;而LDA樣本固定,引數未知但不固定,是個隨機變數,服從一定的分佈,LDA屬於貝葉斯派思想。
pLSA與LDA生成文件方式的對比
pLSA模型按照如下的步驟生成“文件-詞項”:
- 按照概率
選擇一篇文件
- 選定文件
後,確定文章的主題分佈
- 從主題分佈中按照概率
選擇一個隱含的主題類別
- 選定
後,確定主題下的詞分佈
- 從詞分佈中按照概率
選擇一個詞
LDA模型中一篇文件生成的方式:
- 按照先驗概率
選擇一篇文件
- 從狄利克雷分佈
中取樣生成文件
的主題分佈
,換言之,主題分佈
由超引數為
的Dirichlet分佈生成
- 從主題的多項式分佈
中取樣生成文件
第 j 個詞的主題
- 從狄利克雷分佈(即Dirichlet分佈)
中取樣生成主題
對應的詞語分佈
,換言之,詞語分佈
由引數為
的Dirichlet分佈生成
- 從詞語的多項式分佈
中取樣最終生成詞語

從上面兩個過程可以看出,LDA在PLSA的基礎上,為主題分佈和詞分佈分別加了兩個Dirichlet先驗(也就是主題分佈的分佈和詞分佈的分佈)。
pLSA與LDA的概率圖對比
pLSA跟LDA生成文件的不同過程,左圖是pLSA,右圖是LDA(右圖不太規範,z跟w都得是小寫):LDA概率圖: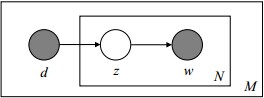
對應到上面右圖的LDA,只有W / w是觀察到的變數,其他都是隱變數或者引數,其中,Φ表示詞分佈,Θ表示主題分佈,
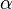 是主題分佈Θ的先驗分佈(即Dirichlet 分佈)的引數,
是主題分佈Θ的先驗分佈(即Dirichlet 分佈)的引數,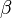 是詞分佈Φ的先驗分佈的引數,N表示文件的單詞總數,M表示文件的總數。
是詞分佈Φ的先驗分佈的引數,N表示文件的單詞總數,M表示文件的總數。- 假定語料庫中共有M篇文章,每篇文章下的Topic的主題分佈是一個從引數為
的Dirichlet先驗分佈中取樣得到的Multinomial分佈,每個Topic下的詞分佈是一個從引數為
的Dirichlet先驗分佈中取樣得到的Multinomial分佈。
- 對於某篇文章中的第n個詞,首先從該文章中出現的每個主題的Multinomial分佈(主題分佈)中選擇或採樣一個主題,然後再在這個主題對應的詞的Multinomial分佈(詞分佈)中選擇或採樣一個詞。不斷重複這個隨機生成過程,直到M篇文章全部生成完成。
- 其中,
→θ→z 表示生成文件中的所有詞對應的主題,顯然
→θ 對應的是Dirichlet 分佈,θ→z 對應的是 Multinomial 分佈,所以整體是一個 Dirichlet-Multinomial 共軛結構,如下圖所示:
- 類似的,
→φ→w,容易看出, 此時β→φ對應的是 Dirichlet 分佈, φ→w 對應的是 Multinomial 分佈, 所以整體也是一個Dirichlet-Multinomial 共軛結構,如下圖所示:
pLSA與LDA引數估計方法的對比
假定文件已經產生,反推其主題分佈。那麼,它們估計未知引數所採用的方法有什麼不同?- pLSA中,我們使用EM演算法去估計“主題-詞項”矩陣Φ和“文件-主題”矩陣Θ,而且這兩引數都是個未知的固定的值,使用的思想其實就是極大似然估計MLE。
- LDA中,估計Φ、Θ這兩未知引數可以用變分(Variational inference)-EM演算法,也可以用gibbs取樣,前者的思想是最大後驗估計MAP(MAP與MLE類似,都把未知引數當作固定的值),後者的思想是貝葉斯估計。貝葉斯估計是對MAP的擴充套件,但它與MAP有著本質的不同,即貝葉斯估計把待估計的引數看作是服從某種先驗分佈的隨機變數。
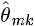 、
、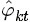 。LDA中,主題分佈和詞分佈本身都是多項分佈,而由上文可知“Dirichlet分佈是多項式分佈的共軛先驗概率分佈”,因此選擇Dirichlet 分佈作為它們的共軛先驗分佈。意味著為多項分佈的引數p選取的先驗分佈是Dirichlet分佈,那麼以p為引數的多項分佈用貝葉斯估計得到的後驗分佈仍然是Dirichlet分佈。
。LDA中,主題分佈和詞分佈本身都是多項分佈,而由上文可知“Dirichlet分佈是多項式分佈的共軛先驗概率分佈”,因此選擇Dirichlet 分佈作為它們的共軛先驗分佈。意味著為多項分佈的引數p選取的先驗分佈是Dirichlet分佈,那麼以p為引數的多項分佈用貝葉斯估計得到的後驗分佈仍然是Dirichlet分佈。PLSA與LDA的本質區別詳解及例項*
- PLSA中,主題分佈和詞分佈是唯一確定的,能明確的指出主題分佈可能就是{教育:0.5,經濟:0.3,交通:0.2},詞分佈可能就是{大學:0.5,老師:0.3,課程:0.2}。
- LDA中,主題分佈和詞分佈不再唯一確定不變,即無法確切給出。例如主題分佈可能是{教育:0.5,經濟:0.3,交通:0.2},也可能是{教育:0.6,經濟:0.2,交通:0.2},到底是哪個我們不再確定,因為它是隨機的可變化的。但再怎麼變化,也依然服從一定的分佈,即主題分佈跟詞分佈由Dirichlet先驗隨機確定。面對多個主題或詞,各個主題或詞被抽中的概率不一樣,所以抽取主題或詞是隨機抽取。主題分佈和詞分佈本身也都是不確定的,正因為LDA是PLSA的貝葉斯版本,所以主題分佈跟詞分佈本身由先驗知識隨機給定。
- pLSA中,主題分佈和詞分佈確定後,以一定的概率(
、
)分別選取具體的主題和詞項,生成好文件。而後根據生成好的文件反推其主題分佈、詞分佈時,最終用EM演算法(極大似然估計思想)求解出了兩個未知但固定的引數的值:
(
)和
(
)
- 舉個文件d產生主題z的例子。給定一篇文件d,主題分佈是一定的,比如{ P(zi|d), i = 1,2,3 }={0.4,0.5,0.1},表示z1、z2、z3,這3個主題被文件d選中的概率都是個固定的值:P(z1|d) = 0.4、P(z2|d) = 0.5、P(z3|d) = 0.1。
- 貝葉斯框架下的LDA中,我們不再認為主題分佈和詞分佈是唯一確定的(而是隨機變數),而是有很多種可能。LDA為它們弄了兩個Dirichlet先驗引數,為某篇文件隨機抽取出某個主題分佈和詞分佈。
- 文件d產生主題z(準確的說,其實是Dirichlet先驗為文件d生成主題分佈Θ,然後根據主題分佈Θ產生主題z)的概率,主題z產生單詞w的概率都不再是某兩個確定的值,而是隨機變數。
- 例子:給定一篇文件d,現在有多個主題z1、z2、z3,它們的主題分佈{ P(zi|d), i = 1,2,3 }可能是{0.4,0.5,0.1},也可能是{0.2,0.2,0.6},即這些主題被d選中的概率都不再認為是確定的值,而主題分佈到底是哪個取值集合我們不確定(這就是貝葉斯派的核心思想,把未知引數當作是隨機變數,不再認為是某一個確定的值),但其先驗分佈是dirichlet 分佈,所以可以從無窮多個主題分佈中按照dirichlet 先驗隨機抽取出某個主題分佈出來。
- 文件d產生主題z(準確的說,其實是Dirichlet先驗為文件d生成主題分佈Θ,然後根據主題分佈Θ產生主題z)的概率,主題z產生單詞w的概率都不再是某兩個確定的值,而是隨機變數。
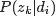 、
、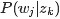 )加了兩個先驗分佈的引數(貝葉斯化):一個主題分佈的先驗分佈Dirichlet分佈
)加了兩個先驗分佈的引數(貝葉斯化):一個主題分佈的先驗分佈Dirichlet分佈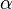 ,和一個詞語分佈的先驗分佈Dirichlet分佈
,和一個詞語分佈的先驗分佈Dirichlet分佈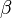 。
。LDA是pLSA的generalization:一方面LDA的hyperparameter設為特定值的時候,就specialize成pLSA了。從工程應用價值的角度看,這個數學方法的generalization,允許我們用一個訓練好的模型解釋任何一段文字中的語義。而pLSA只能理解訓練文字中的語義。(雖然也有ad hoc的方法讓pLSA理解新文字的語義,但是大都效率低,並且並不符合pLSA的數學定義。)
綜上,LDA真的只是pLSA的貝葉斯版本,文件生成後,兩者都要根據文件去推斷其主題分佈和詞語分佈(即兩者本質都是為了估計給定文件生成主題,給定主題生成詞語的概率),只是用的引數推斷方法不同,在pLSA中用極大似然估計的思想去推斷兩未知的固定引數,而LDA則把這兩引數弄成隨機變數,且加入dirichlet先驗。 所以,pLSA跟LDA的本質區別就在於它們去估計未知引數所採用的思想不同,前者用的是頻率派思想,後者用的是貝葉斯派思想。
LDA生成文件過程的進一步理解
LDA主題分佈中比如{ P(zi), i =1,2,3 }等於{0.4,0.5,0.1}或{0.2,0.2,0.6}是由dirichlet先驗給定的,不是根據文件產生的。所以,LDA生成文件的過程中,先從dirichlet先驗(主題分佈的分佈)中“隨機”抽取出主題分佈,然後從主題分佈中“隨機”抽取出主題,最後從確定後的主題對應的詞分佈中“隨機”抽取出詞。Dirichlet先驗是如何“隨機”抽取主題分佈的
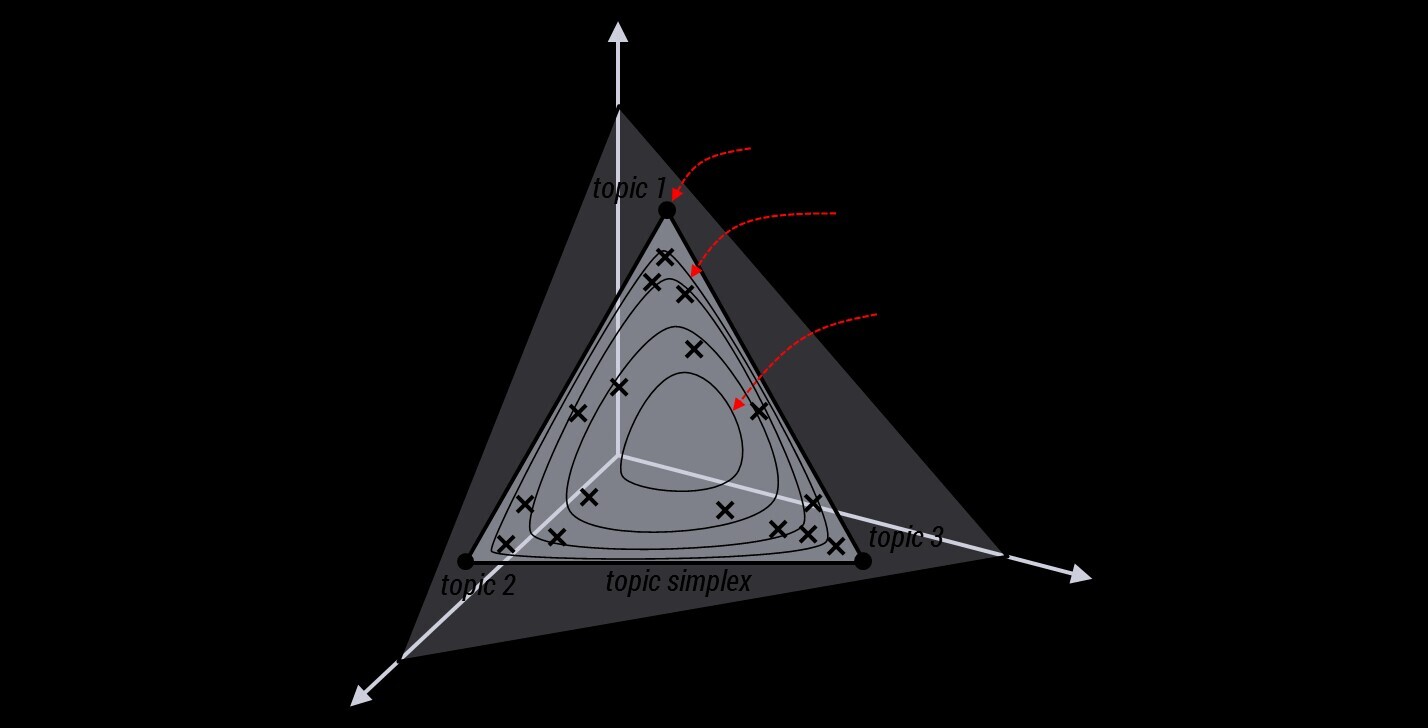
事實上,從dirichlet分佈中隨機抽取主題分佈,這個過程不是完全隨機的。為了說清楚這個問題,咱們得回顧下dirichlet分佈。事實上,如果我們取3個事件的話,可以建立一個三維座標系,類似xyz三維座標系,這裡,我們把3個座標軸弄為p1、p2、p3,如下圖所示:
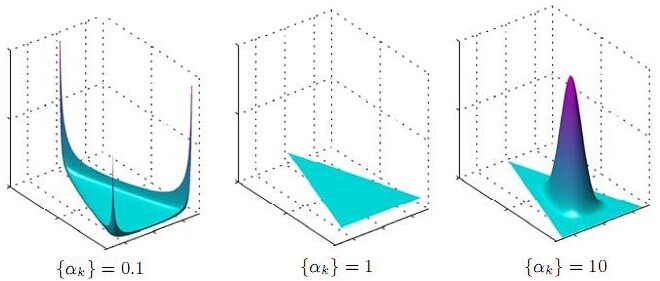
在這個三維座標軸所劃分的空間裡,每一個座標點(p1,p2,p3)就對應著一個主題分佈,且某一個點(p1,p2,p3)的大小表示3個主題z1、z2、z3出現的概率大小(因為各個主題出現的概率和為1,所以p1+p2+p3 = 1 {三角平面},且p1、p2、p3這3個點最大取值為1)。比如(p1,p2,p3) = (0.4,0.5,0.1)便對應著主題分佈{ P(zi), i =1,2,3 } = {0.4,0.5,0.1},空間裡有很多這樣的點(p1,p2,p3),意味著有很多的主題分佈可供選擇,那dirichlet分佈如何選擇主題分佈呢?把上面的斜三角形放倒,對映到底面的平面上,便得到如下所示的一些彩圖(3個彩圖中,每一個點對應一個主題分佈,高度代表某個主題分佈被dirichlet分佈選中的概率,且選不同的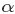
Note:
1 上圖的繪製大概這樣:alpha=0.1固定時,dirichlet分佈的概率密度函式就固定了

這個概率密度在x1或x2或x3為1,其餘為0時的概率最大,x1=x2=x3時概率最小,也就是上圖1所示的了。
2 alpha=0.1到10看出,alpha越大,選出的主題分佈越傾向於均勻分佈(也就是主題分佈是均勻相等的概率最大)。
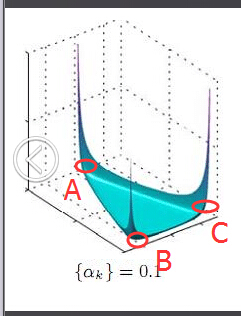
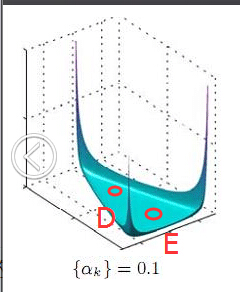
所以雖然說dirichlet分佈是隨機選取任意一個主題分佈的,但依然存在著P(A) = P(B) = P(C) >> P(D) = P(E),即dirichlet分佈還是“偏愛”某些主題分佈的。至於dirichlet分佈的引數
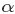 是如何決定dirichlet分佈的形狀的,可以從dirichlet分佈的定義和公式思考。 此外,就算說“隨機”選主題也是根據主題分佈來“隨機”選取,這裡的隨機不是完全隨機的意思,而是根據各個主題出現的概率值大小來抽取。比如當dirichlet先驗為文件d生成的主題分佈{ P(zi), i =1,2,3 }是{0.4,0.5,0.1}時,那麼主題z2在文件d中出現的概率便是0.5。
是如何決定dirichlet分佈的形狀的,可以從dirichlet分佈的定義和公式思考。 此外,就算說“隨機”選主題也是根據主題分佈來“隨機”選取,這裡的隨機不是完全隨機的意思,而是根據各個主題出現的概率值大小來抽取。比如當dirichlet先驗為文件d生成的主題分佈{ P(zi), i =1,2,3 }是{0.4,0.5,0.1}時,那麼主題z2在文件d中出現的概率便是0.5。皮皮Blog
LDA引數估計:Gibbs取樣
理解這一節,需要先看懂吉布斯取樣演算法。
類似於pLSA,LDA的原始論文中是用的變分-EM演算法估計未知引數,但不太好理解,並且EM演算法可能推匯出區域性最優解。後來發現另一種估計LDA未知引數的方法更好,Heinrich使用了Gibbs抽樣法。Gibbs抽樣是馬爾可夫鏈蒙特卡爾理論(MCMC)中用來獲取一系列近似等於指定多維概率分佈(比如2個或者多個隨機變數的聯合概率分佈)觀察樣本的演算法。
LDA Gibbs Sampler
為了構造LDA Gibbs抽樣器,我們需要使用隱變數的Gibbs抽樣器公式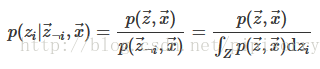
(lz:這裡分母實際只是分子對zi的一個積分,將變數zi積分掉,就得到p(z-i, x),所以重點在聯合分佈p(z,w)公式上,一般先推出聯合分佈公式再積分就可以使用上面的隱變數gibbs取樣公式了。而這個聯合分佈就是我們取樣出來的結果推斷出的近似分佈,也就是下面LDA所有變數的聯合分佈如何通過取樣結果求解出來)。
在LDA模型中,隱變數為zm,n,即樣本中每個詞wm,n所屬的主題,而引數Θ和Φ等可以通過觀察到的wm,n和相應的zm,n積分求得,這種處理方法稱作collapsed,在Gibbs sampling中經常使用。
要推斷的目標分佈p(z|w)(後驗概率分佈),它和聯合分佈成正比 p(z|w)=p(z,w)p(w)=∏Wi=1p(zi,wi)∏Wi=1∑Kk=1p(zi=k,wi) {這裡省略了超引數},這個分佈涉及很多離散隨機變數,並且分母是KW個項的求和,很難求解(正如從一維均勻分佈取樣很容易,直接從二維均勻分佈取樣就比較困難了,也是通過固定某個維度gibbs取樣的)。此時,就需要Gibbs sampling發揮用場了,我們期望Gibbs抽樣器可以通過Markov鏈利用全部的條件分佈p(zi|z¬i,w) 來模擬p(z|w) 。
LDA所有變數的聯合分佈
聯合概率分佈p(w,z): p(w,z|α,β)=p(w|z,β)p(z|α)
給定一個文件集合,w是可以觀察到的已知變數,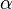 和
和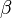 是根據經驗給定的先驗引數,其他的變數z,θ和φ都是未知的隱含變數,需要根據觀察到的變數來學習估計的。根據LDA的圖模型,可以寫出所有變數的聯合分佈:
是根據經驗給定的先驗引數,其他的變數z,θ和φ都是未知的隱含變數,需要根據觀察到的變數來學習估計的。根據LDA的圖模型,可以寫出所有變數的聯合分佈: 因為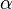
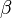
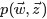
(從概率圖表示中也可以看出)
由於此公式第一部分獨立於 α⃗ ,第二部分獨立於 β⃗ ,所以可以分別處理。計算的兩個未知引數:第一項因子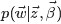
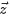
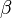
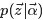
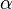
取樣詞過程
第一個因子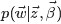
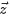
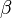
由於樣本中的詞服從引數為主題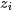
其中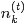
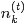
Note:
1 每個主題下包含所有詞,所有詞都要考慮,只是概率不一樣而已。並且這裡的w和z上面都有箭頭,都是向量。
2 初始時每個詞w隨機分配主題k,這樣每個主題下的詞也就隨機分配了,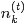
回到第一個因子上來,目標分佈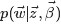
(68)
其中在定義的Dirichlet 分佈的歸一化係數
的公式
(兩種表達方式,其中int表示積分)
這個結果可以看作K個Dirichlet-Multinomial模型的乘積。
Note: 推導:
取樣主題過程
類似,對於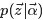
其中,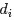
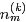
對主題分佈Θ積分可得聯合分佈因子2:
(72)
Note: 上式推導:
綜合第一個因子和第二個因子的結果,得到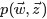
通過聯合分佈公式就可以得出出下面的條件分佈的公式,對每個單詞的主題進行取樣。
LDA詞的主題取樣
通過聯合分佈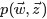 來計算在給定可觀測變數 w 下的隱變數 z 的條件分佈(後驗分佈)
來計算在給定可觀測變數 w 下的隱變數 z 的條件分佈(後驗分佈)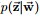 ,再進行貝葉斯分析。換言之,有了這個聯合分佈後,要求解第m篇文件中的第n個詞(下標為
,再進行貝葉斯分析。換言之,有了這個聯合分佈後,要求解第m篇文件中的第n個詞(下標為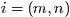 的詞)的全部條件概率就好求了。 變數定義:
的詞)的全部條件概率就好求了。 變數定義: 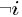 表示除去
表示除去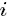 的詞,
的詞,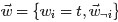 ,
,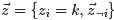 排除當前詞的主題分配,即根據其他詞的主題分配和觀察到的單詞來計算當前詞主題的概率公式為:
排除當前詞的主題分配,即根據其他詞的主題分配和觀察到的單詞來計算當前詞主題的概率公式為:
lz Note:1 各符號表示含義公式(80)
理解的一個重要前提是,單詞庫中的每個單詞w都分配了一個不同的主題z。w:資料集Dt中所有詞;m:文件;k:主題; t:當前詞例項wi = t(特指時)。我們需要求的實際是p(z, w)的聯合分佈,也就是(z, w)的概率分佈,表示每個詞對應的主題是什麼,怎麼求當然是通過含隱變數的gibbs取樣公式取樣,直接通過前面求出的p(w,z)當然是沒法直接取樣,畢竟高維,wz的情況太多。對某個詞wi進行主題分配時,即求(z, w)的分佈時,可以通過排除當前詞的主題分配,根據其他詞的主題分配和觀察到的單詞(z-i, w-i)來計算當前詞主題的概率公式,這也就是含隱含變數的gibbs取樣。p(zi | z-i, w)是wi屬於指定主題zi = k的概率,我們要計算所有的p(zi | z-i, w),歸一化就組成了一個可對wi進行主題取樣的概率分佈了。
-i除去當前詞i相關的不考慮where n−i is the count excluding the current assignment of z i , i.e., z −i .;n−i denotes a quantity excluding the current instance;
z−i代表不是wi的其它所有單詞對應的不同主題組成的集合(類似式68中nz的定義)。p(w|z) 表示所有不同單詞在所有不同主題下概率和偽概率的某種複雜乘積(式68 p(z|w, β)),而p(w-i | z-i)表示的是除了單詞i外的所有其它不同單詞在所有不同主題下的乘積;p(z) 表示所有不同主題在不同文件中概率和偽概率的某種複雜乘積(式72 p(z | α));而p(z-i)表示除了詞wi對應的主題外,其它所有不同主題在所有不同文件中的乘積。
n(t)k,-i表示主題k中單詞t(除了單詞wi外,wi也是詞t1,注意不在和式中的t是指wi等於的單詞t)的個數;而n(t)k表示主題k中單詞t的個數;
n(k)m,-i表示文件m中所有詞(不包括wi)被賦予主題k的次數(其中對於wi所在的主題k, n(k)m, -i = n(k)m - 1;對於wi不在的主題,兩者當然相等);
給個示例吧

2 上式推導:

在此可以直接省略第2個分母,因為它表示的是文件中所有主題的個數,即單詞個數(因為每個單詞都被分配了一個主題嘛),就得到公式最後一個正比式了。另外如果不省略上式右部分母,也可以得到下面的正比等式:
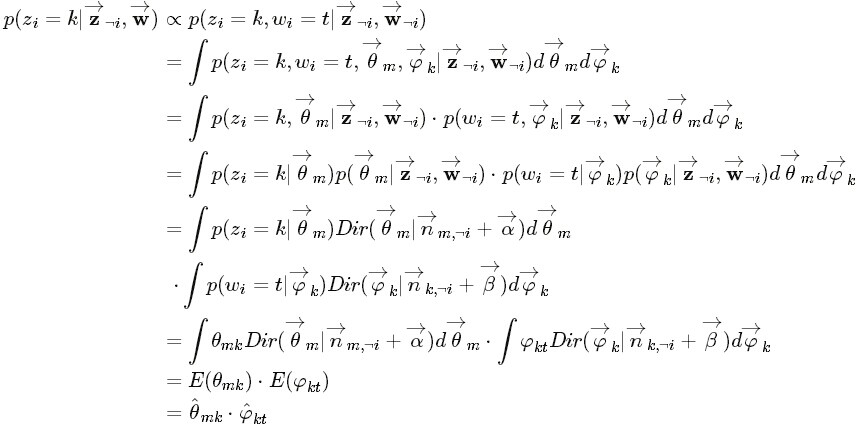 公式(81)
公式(81)Note:不必使用這個公式進行取樣,這個公式只是下面解釋LDA吉布斯取樣圖解過程時比較方便。3 倒數第二步,可以看出,wi(=t)被賦予主題k的概率為 所有詞t在主題k中的概率*主題k中的詞個數在整個文件中的概率。(即主題k上詞t的概率越大,且文件m中的其它詞(-i)被賦予主題k的概率越大,那麼文件m中的詞wi被賦予主題k的概率就越大);
這就是罐子模型!richer get richer!

主題分佈引數Θ和詞分佈引數Φ的計算
Note: LDA的原始論文中,主題的詞分佈通常叫β,但是在許多後來的論文中叫φ,如on smoothing and inference for topic models.
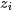 獲取主題分佈的引數Θ和詞分佈的引數Φ(知道了每篇文件下每個詞對應的主題,那麼文件下的主題分佈和主題的詞分佈就好求了)。思路:引數是通過貝葉斯方法求的,先計算 文件m中主題的概率分佈,再取其均值作為引數的估計值。根據貝葉斯法則和Dirichlet先驗,以及上文中得到的
獲取主題分佈的引數Θ和詞分佈的引數Φ(知道了每篇文件下每個詞對應的主題,那麼文件下的主題分佈和主題的詞分佈就好求了)。思路:引數是通過貝葉斯方法求的,先計算 文件m中主題的概率分佈,再取其均值作為引數的估計值。根據貝葉斯法則和Dirichlet先驗,以及上文中得到的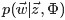 和
和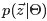 各自被分解成兩部分乘積的結果,可以計算得到每個文件上Topic的後驗分佈和每個Topic下的詞的後驗分佈分別如下(據上文可知:其後驗分佈跟它們的先驗分佈一樣,也都是Dirichlet 分佈):可知,文件m中主題的概率分佈是 資料學習得到的主題多項式分佈似然*文件m主題分佈的Dir先驗。
各自被分解成兩部分乘積的結果,可以計算得到每個文件上Topic的後驗分佈和每個Topic下的詞的後驗分佈分別如下(據上文可知:其後驗分佈跟它們的先驗分佈一樣,也都是Dirichlet 分佈):可知,文件m中主題的概率分佈是 資料學習得到的主題多項式分佈似然*文件m主題分佈的Dir先驗。
其中,是構成文件m的主題數向量,
是構成主題k的詞項數向量。
文件m主題的概率分佈公式推導如下:
根據Dirichlet 分