主題模型TopicModel:Unigram、LSA、PLSA模型
主題模型歷史
Papadimitriou、Raghavan、Tamaki和Vempala在1998年發表的一篇論文中提出了潛在語義索引。1999年,Thomas Hofmann又在此基礎上,提出了概率性潛在語義索引(Probabilistic Latent Semantic Indexing,簡稱PLSI)。
隱含狄利克雷分配LDA可能是最常見的主題模型,是一般化的PLSI,由Blei, David M.、吳恩達和Jordan, Michael I於2003年提出。LDA允許文件擁有多種主題。其它主體模型一般是在LDA基礎上改進的。例如Pachinko分佈在LDA度量詞語關聯之上,還加入了主題的關聯度。
文字建模-理解LDA模型的基礎模型
Unigram model、mixture of unigrams model,以及pLSA模型。
定義變數:
表示詞,
表示所有單詞的個數(固定值)
表示主題,
是主題的個數(預先給定,固定值)
表示語料庫,其中的
是語料庫中的文件數(固定值)
表示文件,其中的
表示一個文件中的詞數(隨機變數)
一元模型Unigram model
{給定文件,同時也給定主題}
對於文件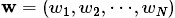
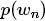


其圖模型為(圖中被塗色的w表示可觀測變數,N表示一篇文件中總共N個單詞,M表示M篇文件):
unigram model假設文字中的詞服從Multinomial分佈,而我們已經知道Multinomial分佈的先驗分佈為Dirichlet分佈。
上圖中的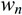
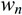
假設我們的詞典中一共有

上帝的這個唯一的骰子各個面的概率記為
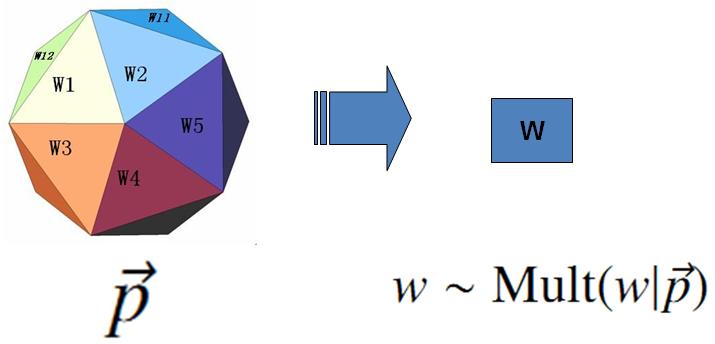
上帝投擲
對於一篇文件
而文件和文件之間我們認為是獨立的, 所以如果語料中有多篇文件
在 Unigram Model 中假設了文件之間是獨立可交換的,而文件中的詞也是獨立可交換的,所以一篇文件相當於一個袋子,裡面裝了一些詞,而詞的順序資訊就無關緊要了,這樣的模型也稱為詞袋模型(Bag-of-words)。
假設語料中總的詞頻是
當然,我們很重要的一個任務就是估計模型中的引數
混合一元模型Mixture of unigrams model
{主題未給定,只是一篇文件只有一個主題}
一篇文件只由一個主題生成。該模型的生成過程是:給某個文件先選擇一個主題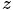 ,再根據該主題生成文件,該文件中的所有詞都來自一個主題。假設主題有
,再根據該主題生成文件,該文件中的所有詞都來自一個主題。假設主題有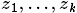 ,生成文件{語料}
,生成文件{語料} 的概率為:
的概率為:其圖模型為(圖中被塗色的w表示可觀測變數,未被塗色的z表示未知的隱變數,N表示一篇文件中總共N個單詞,M表示M篇文件):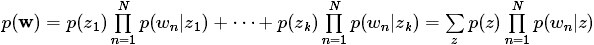
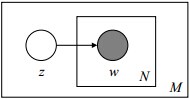
Note: 這個圖的意思是,對一篇文件中的詞,都是由一個主題z(放在小方框外面了)產生。
貝葉斯觀點下的 Unigram Model
{看下面的p(W)公式,這個應該是混合一元模型的連續變數版?}
對於以上模型,貝葉斯統計學派的統計學家會有不同意見,他們會很挑剔的批評只假設上帝擁有唯一一個固定的骰子是不合理的。在貝葉斯學派看來,一切引數都是隨機變數,以上模型中的骰子

上帝的這個罈子裡面,骰子可以是無窮多個,有些型別的骰子數量多,有些型別的骰子少,所以從概率分佈的角度看,罈子裡面的骰子
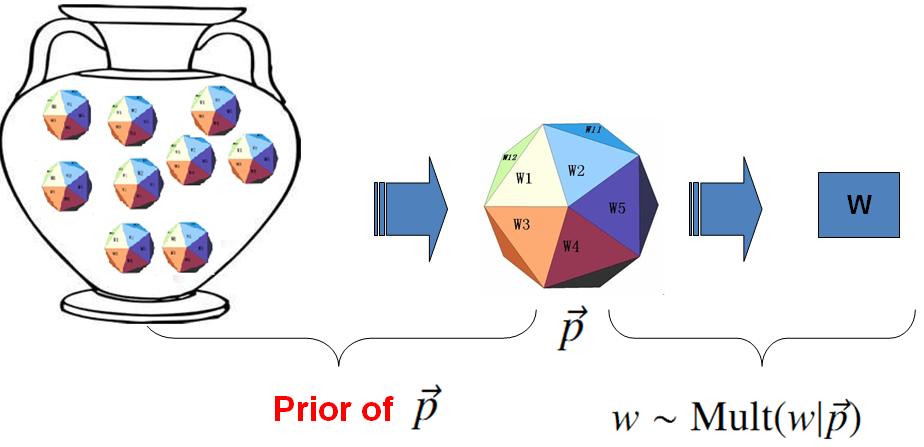
Dirichlet 先驗下的 Unigram Model
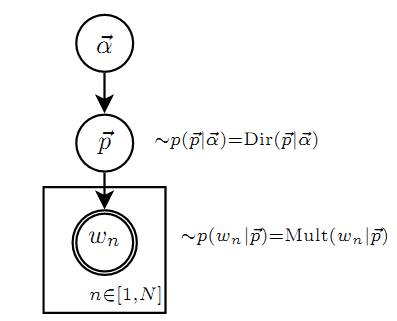
Unigram Model的概率圖模型
其中,p和α是隱含未知變數:
- p是詞服從的Multinomial分佈的引數
- α是Dirichlet分佈(即Multinomial分佈的先驗分佈)的引數。
- 一般α由經驗事先給定,p由觀察到的文字中出現的詞學習得到,表示文字中出現每個詞的概率。
以上貝葉斯學派的遊戲規則的假設之下,語料