增強影象對比度演算法原理及matlab程式碼實現
- clc;
- close all;
- clear all;
- % -------------Gamma Transformations-----------------
- %f = imread('Fig0316(4)(bottom_left).tif');
- f = imread('seed.tif');
- Gamma = 0.4;
- g2 = myExpEnhance(f,Gamma);
- figure();
-
subplot(221); imshow(f); xlabel('a).Original Image');
- subplot(222),imhist(f),title('原影象直方圖');%顯示原始影象直方圖
- subplot(223); imshow(g2); xlabel('b).Gamma Transformations \gamma = 0.4');
- subplot(224),imhist(g2),title('增強影象直方圖');%顯示原始影象直方圖
- function dst_img=myExpEnhance(src_img,Gamma)
-
src_img = mat2gray(src_img,[0 255]);%將影象矩陣A中介於amin和amax的資料歸一化處理, 其餘小於amin的元素都變為0, 大於amax的元素都變為1。
- C = 1;
- g2 = C*(src_img.^Gamma);
- %反歸一化
- max=255;
- min=0;
- dst_img=uint8(g2*(max-min)+min);
三,對數變換
對數變換主要用於將影象的低灰度值部分擴充套件,將其高灰度值部分壓縮,以達到強調影象低灰度部分的目的。變換方法由下式給出。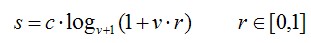
這裡的對數變換,底數為(v+1),實際計算的時候,需要用換底公式。其輸入範圍為歸一化的【0-1】,其輸出也為【0-1】。對於不同的底數,其對應的變換曲線如下圖所示。
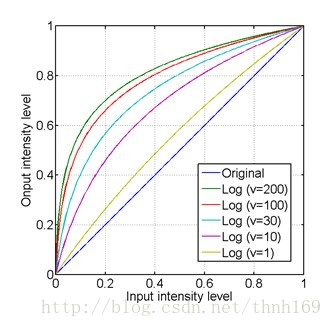
底數越大,對低灰度部分的強調就越強,對高灰度部分的壓縮也就越強。相反的,如果想強調高灰度部分,則用反對數函式就可以了。看下面的實驗就可以很直觀的理解,下圖是某影象的二維傅立葉變換影象,其為了使其灰度部分較為明顯,一般都會使用灰度變換處理一下。

參考程式碼:
- clc;
- close all;
- clear all;
- %-------------Log Transformations-----------------
- f = imread('seed.tif');
- g_1 = myLogEnhance(f,10);
- g_2 = myLogEnhance(f,100);
- g_3 = myLogEnhance(f,200);
- figure();
- subplot(2,2,1);
- imshow(f);xlabel('a).Original Image');
- subplot(2,2,2);
- imshow(g_1);xlabel('b).Log Transformations v=10');
- subplot(2,2,3);
- imshow(g_2);xlabel('c).Log Transformations v=100');
- subplot(2,2,4);
- imshow(g_3);
- xlabel('d).Log Transformations v=200');
對數變換核心函式
- function dst_img=myLogEnhance(src_img,v)
- c=1.0;
- src_img = mat2gray(src_img,[0 255]);
- g =c*log2(1 + v*src_img)/log2(v+1);
- %反歸一化
- max=255;
- min=0;
- dst_img=uint8(g*(max-min)+min);
四,灰度拉伸
灰度拉伸也用於強調影象的某個部分,與伽馬變換與對數變換不同的是,灰度拉昇可以改善影象的動態範圍。可以將原來低對比度的影象拉伸為高對比度影象。實現灰度拉昇的方法很多,其中最簡單的一種就是線性拉伸。而這裡介紹的方法稍微複雜一些。灰度拉伸所用數學式如下所示。
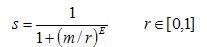
同樣的,其輸入r為【0-1】,其輸出s也為【0-1】。這個式子再熟悉不過了,跟巴特沃斯高通濾波器像極了,其輸入輸出關係也大致能猜到是個什麼形狀的。但是,這裡就出現一個問題了,輸入為0時候,式子無意義了。所以,在用Matlab計算的時候,將其變為如下形式。
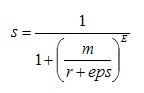
這裡的eps,就是Matlab裡面,一個很小數。如此做的話,式子變得有意義了。但是,其輸入範圍為【0-1】的時候,其輸出範圍變為了
 。輸出範圍大致為【0-1】,為了精確起見,使用mat2gray函式將其歸一化到精確的[0-1]。呼叫格式如下。
。輸出範圍大致為【0-1】,為了精確起見,使用mat2gray函式將其歸一化到精確的[0-1]。呼叫格式如下。
五,線性拉伸
為了突出感興趣的目標或者灰度區間,相對抑制那些不感興趣的灰度區域,可採用分段線性法,常用的是三段線性變換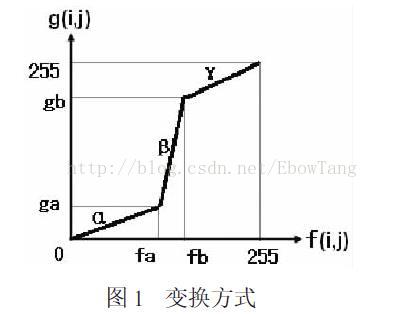
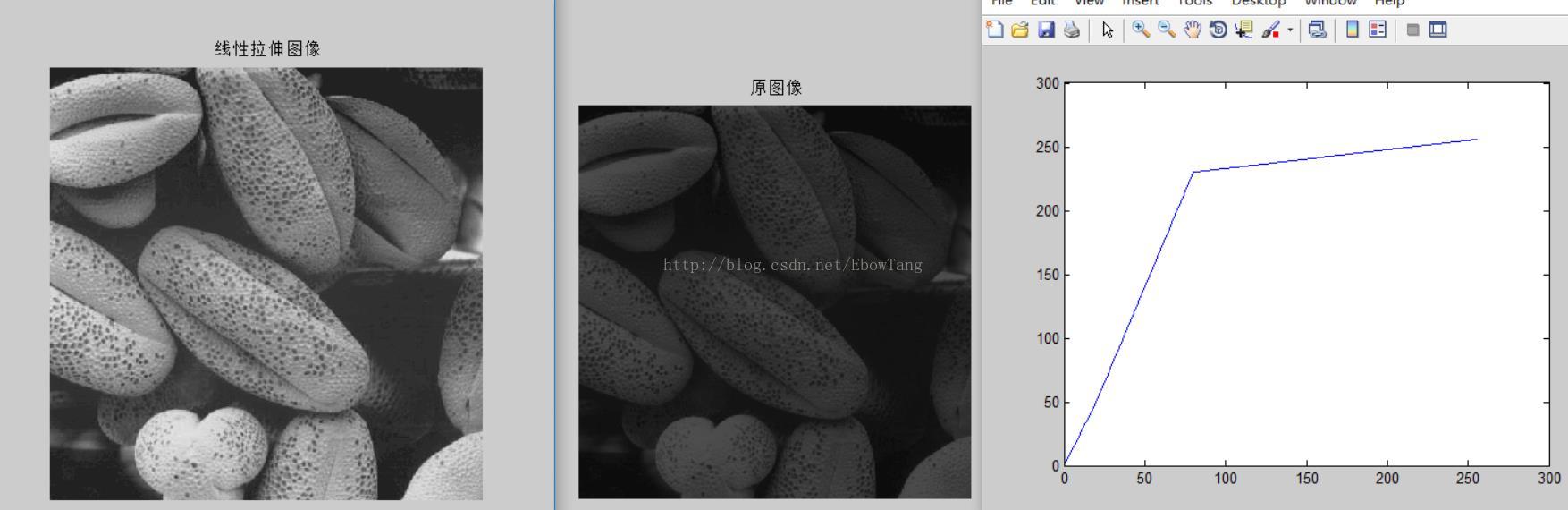
參考程式:
- clc;
- close all;
- clear all;
- I=imread('seed.tif');
- [m,n,k]=size(I);
- figure (1)
- imshow('seed.tif');title(' 原影象');
- mid=mean(mean(I));
- %橫軸
- fa=20; fb=80;
- %縱軸
- ga=50; gb=230;
- J=myLinearEnhance(I,fa,fb,ga,gb);
- figure (2)
- imshow(J);title(' 線性拉伸影象');
- pixel_f=1:256;
- pixel_g=zeros(1,256);
- %三段斜率,小於1表示該段將會被收縮
- k1=double(ga/fa);
- k2=(gb- ga)/(fb- fa);
- k3=(256- gb)/(256- fb);
- for i=1:256
- if i <= fa
- pixel_g(i)= k1*i;
- elseif fa < i && i <= fb
- pixel_g(i)= k2*( i- fa)+ ga;
- else
- pixel_g(i)= k3*( i - fb)+ gb;
- end
- end
- figure (3)
- plot(pixel_f,pixel_g);
核心函式:
- function dst_img=myLinearEnhance(src_img,fa,fb,ga,gb)
- [height,width] = size(src_img);
- dst_img=uint8(zeros(height,width));
- src_img=double(src_img);
- %三段斜率
- k1=ga/fa;
- k2=(gb- ga)/(fb- fa);
- k3=(255- gb)/(255- fb);
- for i=1:height
- for j=1:width
- if src_img(i,j) <= fa
- dst_img(i,j)= k1*src_img(i,j);
- elseif fa < src_img(i,j) && src_img(i,j) <= fb
- dst_img(i,j)= k2*( src_img(i,j)- fa)+ ga;
- else
- dst_img(i,j)= k3*( src_img(i,j)- fb)+ gb;
- end
- end
- end
- dst_img=uint8(dst_img);
附錄:
附錄網上的另一份講解:
直方圖均衡化演算法分為三個步驟,第一步是統計直方圖每個灰度級出現的次數,第二步是累計歸一化的直方圖,第三步是計算新的畫素值。
第一步:
for(i=0;i<height;i++)
for(j=0;j<width;j++)
n[s[i][j]]++;
for(i=0;i<L;i++)
p[i]=n[i]/(width*height);
這裡,n[i]表示的是灰度級為i的畫素的個數,L表示的是最大灰度級,width和height分別表示的是原始影象的寬度和高度,所以,p[i]表示的就是灰度級為i的畫素在整幅影象中出現的概率(其實就是p[]這個陣列儲存的就是這幅影象的歸一化之後的直方圖)。
第二步:
for(i=0;i<=L;i++)
for(j=0;j<=i;j++)
c[i]+=p[j];
c[]這個陣列儲存的就是累計的歸一化直方圖。
第三步:
max=min=s[0][0];
for(i=0;i<height;i++)
for(j=0;j<width;j++)
if(max<s[i][j]){
max=s[i][j];
}else if(min>s[i][j]){
min=s[i][j];
}
找出畫素的最大值和最小值。
for(i=0;i<height;i++)
for(j=0;j<width;j++)
t[i][j]=c[s[i][j]]*(max-min)+min;
t[][]就是最終直方圖均衡化之後的結果。
收錄優秀程式碼:
這份程式碼寫得不錯,學習了,原部落格地址見參考資源【3】!
-
相關推薦
增強影象對比度演算法原理及matlab程式碼實現
clc; close all; clear all; % -------------Gamma Transformations----------------- %f = imread('Fig0316(4)(bottom_left).tif');
影象去霧之何凱明暗通道先驗去霧演算法原理及c++程式碼實現
http://blog.csdn.net/s12244315/article/details/50292049 何凱明博士,2007年清華大學畢業,2011年香港中文大學博士畢業,可謂是功力深厚,感嘆於國內一些所謂博士的水平,何這樣的博士才可以真正叫做
最短路徑A*演算法原理及java程式碼實現(看不懂是我的失敗)
package astar; import java.util.ArrayList; import java.util.Collections; import java.util.Comparator; import java.util.HashMap; import java.util.List; imp
常見排序演算法原理及JS程式碼實現
[toc] `建立時間:2020-08-07` 本文只是將作者學習的過程以及演算法理解進行簡單的分享,提供多一個角度的理解說明,或許讓你的困惑能得以解決(**程式碼或說明若有問題,歡迎留言、聯絡更正!以免造成更多困惑**) 如果要更深入研究這些演算法的同學,社群中同類型更優秀,單個演算法更深入剖析的文章
區域生長演算法原理及MATLAB實現
% Segment based on area, Region Growing; clear all; close all; clc [fileName,pathName] = uigetfile('*.*','Please select an image');%檔案筐,選擇檔案 if(fileName)
人臉表情識別筆記(二)特徵提取之LBP(區域性二值模式)原理及MATLAB程式碼
一:原理部分 LBP(Local Binary Pattern,區域性二值模式)是一種用來描述影象區域性紋理特徵的運算元;它具有旋轉不變性和灰度不變性等顯著的優點。它是首先由T. Ojala, M.Pietikäinen, 和D. Harwood 在1994年提出,用
k-中心點演算法(k-medoids)及Matlab程式碼實現
k-中心點演算法(k-medoids)及Matlab程式碼 1. 提出: k-means演算法是每次選擇簇的均值作為新的中心點,迭代直到簇中心不再變化(趨於穩定)。其缺點是對離群點特別敏感,因為一個很大的極端值物件會扭曲資料分佈,使簇均值嚴重偏離;於是我
斯坦福機器學習筆記1:GDA高斯判別分析演算法的原理及matlab程式實現
ps:我本身沒有系統的學過matlab程式設計,所以有的方法,比如求均值用mean()函式之類的方法都是用很笨的方法實現的,所以有很多需要改進的地方,另外是自學實現的程式,可能有的地方我理解錯誤,如果有錯誤請提出來,大家一起學習,本人qq553566286 首先,本文用到的
LDA演算法原理及matlab實現
注:本文非筆者原創,原文轉載自:http://blog.csdn.net/porly/article/details/8020696 1. LDA是什麼 線性判別式分析(Linear Discriminant Analysis),簡稱為LDA。也稱為Fisher線性
資料探勘之clara演算法原理及例項(程式碼中有bug)
繼上兩篇文章介紹聚類中基於劃分思想的k-means演算法和k-mediod演算法 本文將繼續介紹另外一種基於劃分思想的k-mediod演算法-----clara演算法 clara演算法可以說是對k-mediod演算法的一種改進,就如同k-mediod演算法對 k-m
標記符控制的分水嶺演算法原理及matlab實現
-------------------------------------------------------------------------------------------------------------------- 附錄A 教程【3】給出的mat
深入淺出PID控制演算法(二)————PID演算法離散化和增量式PID演算法原理及Matlab實現
引言 上篇介紹了連續系統的PID演算法,但是計算機控制是一種取樣控制,他只能根據取樣時刻的偏差來計算控制量,因此計算機控制系統中,必須對公式進行離散化,具體就是用求和代替積分,用向後差分來代替微分,使模擬PID離散化為數字形式的差分方程。 準備工
STFT原理及MATLAB程式碼
原文地址:http://blog.csdn.net/shengzhadon/article/details/46811923 一、先說說STFT的理論 1.概念和特點 STFT(short-time Fourier transform,短時傅立葉變換
Canny邊緣檢測演算法原理及C語言實現詳解
Canny運算元是John Canny在1986年提出的,那年老大爺才28歲,該文章發表在PAMI頂級期刊上的(1986. A computational approach to edge detection. IEEE Transactions on Pattern Analy
熵值法的應用及matlab程式碼實現
熵值法是指用來判斷某個指標的離散程度的數學方法。離散程度越大,對該指標對綜合評價的影響越大。可以用熵值判斷某個指標的離散程度。 用 途判斷某個指標的 離散程度 離散程度越大該指標對綜合評價的影響越大 熵&nbs
機器學習系列文章:Apriori關聯規則分析演算法原理分析與程式碼實現
1.關聯規則淺談 關聯規則(Association Rules)是反映一個事物與其他事物之間的相互依存性和關聯性,如果兩個或多個事物之間存在一定的關聯關係,那麼,其中一個事物就能通過其他事物預測到。關聯規則是資料探勘的一個重要技術,用於從大量資料中挖掘出有價值的資料
歸併排序演算法原理分析與程式碼實現
歸併排序是建立在歸併操作上的一種有效的排序演算法。該演算法是採用分治法(Divide and Conquer)的一個非常典型的應用,歸併排序將兩個已排序的表合併成一個表。 歸併排序基本原理
利用霍夫變換做直線檢測的原理及OpenCV程式碼實現
說白了,以直線檢測為例,霍夫變換實際上就是把使每個畫素座標點經過變換都變成都直線特質有貢獻的統一度量(這種度量以我目前的理解與笛卡爾(極坐系)並無區別,即極半徑和極角),並對轉換後的度量進行累計(可以理解為投票),當一個波峰出現時候,說明有直線存在。如果要了解更詳細的,大
影象處理之直方圖均衡MATLAB程式碼實現
MATLAB畫灰度影象直方圖的程式碼 I=imread('cameraman.tif'); [M N]=size(I);%求出圖片大小 y=zeros(1,256) x=0:255; for t=0:255 for i=1:M for j=1:N
引導濾波原理及C++程式碼實現
前置內容 在學習引導濾波,最好對高斯濾波和雙邊濾波有過理解,對於高斯濾波: W i
