最小生成樹(1)--Kruskal演算法
圖的最小生成樹
圖的最小生成樹,是指用最小的邊讓圖連通,讓任意兩點之間可以互相到達。圖如果有n個頂點,則應該有n-1條邊。此時連通無向圖沒有迴路,就是一顆樹,所以稱為最小生成樹。
最小生成樹是讓邊的總長度之和最短,其中一種方法是可以選擇最短的邊,然後依次選擇次短的邊,直到選擇了n-1條邊為止。所以可以先將所有的邊按權值從小到大進行排序(為了排序方便可以用結構體儲存圖的邊值資料),然後再選擇,選擇n-1條邊讓整個圖連通。當然有的權值小的邊是不能選擇的,那些會形成迴路的邊不能選,只能跳過這條邊。
在這個過程中,最難實現的是判斷兩個頂點有沒有連通。可以使用深度優先搜尋或者廣度優先搜尋。不過有更方便的方法,判斷頂點是否連通,可以用並查集查頂點是否有同一個祖先,如果有同一個祖先,就是連通的,如果不是同樣的祖先,就表示沒有連通,就可以選擇這兩個頂點的邊。
舉個栗子:
比如下面的圖,用kruskal演算法找最小生成樹的方法如下。
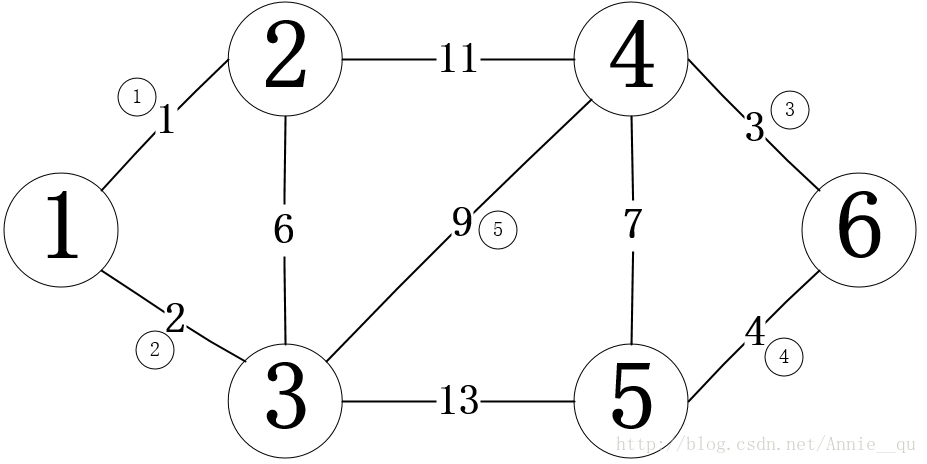
原圖:
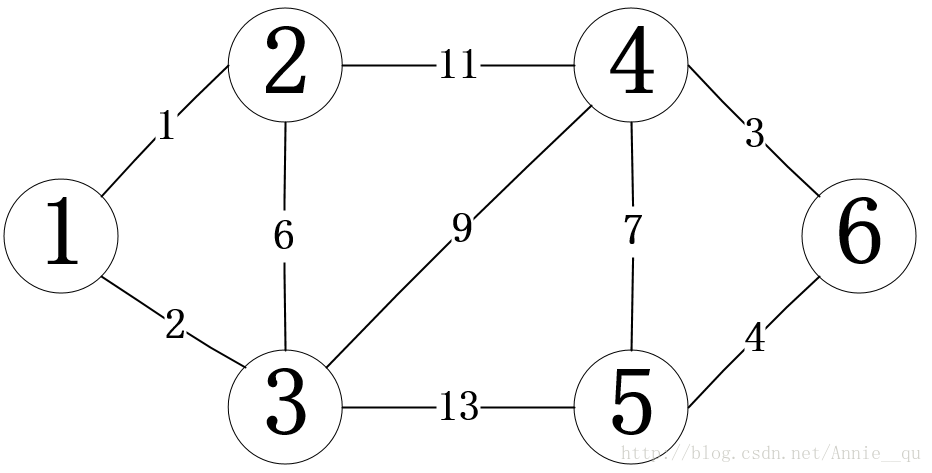
選擇就先找權值最小的邊,很明顯是頂點1和2的權值只有1,而且兩個頂點現在沒有連通,則選擇這條邊將1和2連通。接下來的選擇頂點1和3的邊,權值次小為2,而且此時1和3沒有連通。所以可以選這條邊。如此選擇下去,直到選滿n-1條邊,也就是5條結束。
注意在最後一條邊,也就是下圖的標號5的邊,是1、2、3連通,4、5、6連通時,本來按照從小到大應該玄子頂點4和5的邊為7,但是此時頂點4和5已經通過頂點6連通了,就不需要再選擇這條邊了,也就是我們之前說的通過並查集看是否連通要跳過邊的情況。
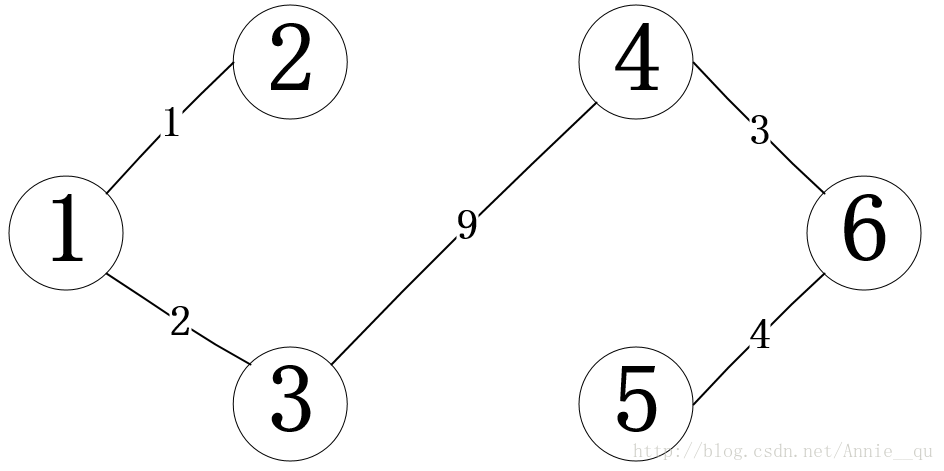
找完所有邊之後,形成的最小生成樹:
接下來小小的略微說一說並查集:
並查集
並查集就像是一片森林,不斷的合併成一棵大樹。要判斷兩個結點是否是同一棵樹,要注意必須求兩個結點的根源,也就是兩個結點的根結點是同一個則在同一個集合中。
所以我們用一個數組表示結點,用陣列的值記錄它的根結點可以不斷更新。首先,我們將結點都當成獨立的,也就是將陣列值初始化為它的下標,用之後按要求將結點合併。合併也就是建立並查集的過程。
怎麼實現呢?
兩個結點用遞迴先搜尋到它的根結點,比較兩個根結點是否相同。如果相同,就不用處理,若不相同,我們就規定靠左,也就是把陣列下標小的作為大的根,就是把陣列右邊的集合,作為左邊集合的子集合。用遞迴的好處還有,在每一次函式返回的時如果根結點有變,則順帶將之前同一棵樹下的結點都改成同一個根。
實現程式碼:
//遞迴尋求結點的祖先
int getf(int v)
{
if(f[v]==v)
return v;
else
{
f[v]=getf(f[v]);
return f[v];
}
}
//合併並查集兩子集
int merge(int u, int v)
{
int comp1,comp2;
comp1=getf(u);
comp2=getf(v);
if(comp1==comp2)
return 0;
else
{
f[comp1]=comp2;
return 1;
}
return 0;
}講好了並查集,我們就可以用並查集來做最小生成樹了。在這裡我們統計一下最小生成樹的邊權值總和。下面貼出例項程式碼:
#include <stdio.h>
#include <stdlib.h>
int n,m,sum,count;
struct edge
{
int u;
int v;
int w;
};
struct edge e[10];
int f[7]={0},book[10];
//快速排序
void quickSorted(int left, int right)
{
int i,j;
struct edge t;
if(left>right)
return;
i = left;
j = right;
while(i!=j)
{
//一定要先從右往左找
while(e[j].w>=e[left].w && i<j)
j--;
while(e[i].w<=e[left].w &&i<j)
i++;
//交換兩數的位置
if(i<j)
{
t=e[i];
e[i]=e[j];
e[j]=t;
}
}
//將基準數歸位
t=e[left];
e[left]=e[i];
e[i]=t;
quickSorted(left,i-1);//遞迴繼續處理左邊的序列
quickSorted(i+1,right);//遞迴繼續處理右邊的序列
return;
}
//遞迴尋求結點的祖先
int getf(int v)
{
if(f[v]==v)
return v;
else
{
f[v]=getf(f[v]);
return f[v];
}
}
//合併並查集兩子集
int merge(int u, int v)
{
int comp1,comp2;
comp1=getf(u);
comp2=getf(v);
if(comp1==comp2)
return 0;
else
{
f[comp1]=comp2;
return 1;
}
return 0;
}
//主程式
int main(void)
{
int i;
//讀入n,m表示頂點個數和邊的條數
printf("Please input the numbers of Graph' vertex and edge divided by a space:\n");
scanf("%d %d",&n,&m);
//輸入邊,儲存邊的關係
printf("Please input the two vertexes and their edge divided by space.\n");
for(i=1;i<=m;i++)
scanf("%d %d %d",&e[i].u,&e[i].v,&e[i].w);
quickSorted(1,m);//將邊進行排序
//並查集初始化
for(i=1;i<=n;i++)
f[i]=i;
//Kruskal演算法
for(i=1;i<=m;i++)
{
//判斷邊的兩個頂點是否連通
if(merge(e[i].u,e[i].v))
{
book[i]=1;//記錄哪些邊構成了最小生成樹
count++;
sum=sum+e[i].w;
}
if(count == n-1)
break;
}
//輸出最小生成樹的邊
printf("Print the smallest tree:\n");
for(i=1;i<=m;i++)
{
if(book[i]==1)
printf("%d %d %d\n",e[i].u,e[i].v,e[i].w);
else
continue;
}
printf("The wight of all: %d.\n",sum);
return 0;
}
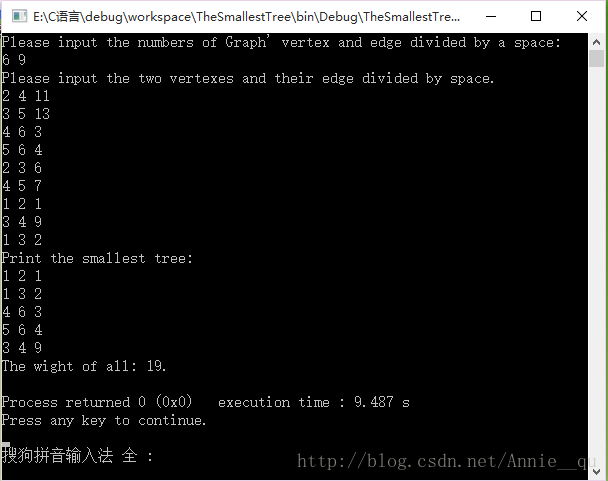
結果:
以上就是最小生成樹的kruskal演算法的內容啦,之後還有最小生成樹的另一種方法Prim演算法,這個和最短路徑的Dijkstra演算法很相似。待續…