最小-最大搜索和Alpha-beta剪枝搜尋
從淺顯的地方開始
在國際象棋裡,雙方棋手都知道每個棋子在哪裡,他們輪流走並且可以走任何合理的著法。下棋的目的就是將死對方,或者避免被將死,或者有時爭取和棋是最好的選擇。 國際象棋程式通過使用“搜尋”函式來尋找著法。搜尋函式獲得棋局資訊,然後尋找對於程式一方來說最好的著法。 一個淺顯的搜尋函式用“樹狀搜尋”(Tree-Searching)來實現。一個國際象棋棋局通常可以看作一個很大的n叉樹(“n叉樹”意思是樹的每個結點有任意多個分枝通向其他結點),棋盤上目前的局面就是“根局面”(Root Position)或“根結點”(Root Node)。從根局面走一步棋,局面就到達根局面的“分枝”(Branch),這些局面稱為“後續局面”(Successor Position)或“後續結點”(Successor Nodes)。每個後續局面後面還有一系列分枝,每個分枝就是這個局面的一個合理的著法。型別:全譯
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Alpha-Beta搜尋 Bruce Moreland / 文 最小-最大的問題 Alpha-Beta 同“最小-最大”非常相似,事實上只多了一條額外的語句。最小最大執行時要檢查整個博弈樹,然後儘可能選擇最好的線路。這是非常好理解的,但效率非常低。每次搜尋更深一層時,樹的大小就呈指數式增長。 通常一個國際象棋局面都有35個左右的合理著法,所以用最小-最大搜索來搜尋一層深度,就有35個局面要檢查,如果用這個函式來搜尋兩層,就有352個局面要搜尋。這就已經上千了,看上去還不怎樣,但是數字增長得非常迅速,例如六層的搜尋就接近是二十億,而十層的搜尋就超過兩千萬億了。 要想通過檢查搜尋樹的前面幾層,並且在葉子結點上用啟發式的評價,那麼做盡可能深的搜尋是很重要的。最小-最大搜索無法做到很深的搜尋,因為有效的分枝因子實在太大了。口袋的例子 幸運的是我們有辦法來減小分枝因子,這個辦法非常可靠,實際上這樣做絕對沒有壞處,純粹是個有益的辦法。這個方法是建立在一個思想上的,如果你已經有一個不太壞的選擇了,那麼當你要作別的選擇並知道它不會更好時,你沒有必要確切地知道它有多壞。有了最好的選擇,任何不比它更好的選擇就是足夠壞的,因此你可以撇開它而不需要完全瞭解它。只要你能證明它不比最好的選擇更好,你就可以完全拋棄它。 你可能仍舊不明白,那麼我就舉個例子。比如你的死敵面前有很多口袋,他和你打賭賭輸了,因此他必須從中給你一樣東西,而挑選規則卻非常奇怪: 每個口袋裡有幾件物品,你能取其中的一件,你來挑這件物品所在的口袋,而他來挑這個口袋裡的物品。你要趕緊挑出口袋並離開,因為你不願意一直做在那裡翻口袋而讓你的死敵盯著你。 假設你一次只能找一隻口袋,在找口袋時一次只能從裡面摸出一樣東西。 很顯然,當你挑出口袋時,你的死敵會把口袋裡最糟糕的物品給你,因此你的目標是挑出“諸多最糟的物品當中是最好的”那個口袋。 你很容易把最小-最大原理運用到這個問題上。你是最大一方棋手,你將挑出最好的口袋。而你的死敵是最小一方棋手,他將挑出最好的口袋裡儘可能差的物品。運用最小-最大原理,你需要做的就是挑一個有“最好的最差的”物品的口袋。 假設你可以估計口袋裡每個物品的準確價值的話,最小-最大原理可以讓你作出正確的選擇。我們討論的話題中,準確評價並不重要,因為它同最小-最大或Alpha-Beta的工作原理沒有關係。現在我們假設你可以正確地評價物品。 最小-最大原理剛才討論過,它的問題是效率太低。你必須看每個口袋裡的每件物品,這就需要花很多時間。 那麼怎樣才能做得比最小-最大更高效呢? 我們從第一個口袋開始,看每一件物品,並對口袋作出評價。比方說口袋裡有一隻花生黃油三明治和一輛新汽車的鑰匙。你知道三明治更糟,因此如果你挑了這隻口袋就會得到三明治。事實上只要我們假設對手也會跟我們一樣正確評價物品,那麼口袋裡的汽車鑰匙就是無關緊要的了。 現在你開始翻第二個口袋,這次你採取的方案就和最小-最大方案不同了。你每次看一件物品,並跟你能得到的最好的那件物品(三明治)去比較。只要物品比三明治更好,那麼你就按照最小-最大方案來辦——去找最糟的,或許最糟的要比三明治更好,那麼你就可以挑這個口袋,它比裝有三明治的那個口袋好。 比方這個口袋裡的第一件物品是一張20美元的鈔票,它比三明治好。如果包裡其他東西都沒比這個更糟了,那麼如果你選了這個口袋,它就是對手必須給你的物品,這個口袋就成了你的選擇。 這個口袋裡的下一件物品是六合裝的流行唱片。你認為它比三明治好,但比20美元差,那麼這個口袋仍舊可以選擇。再下一件物品是一條爛魚,這回比三明治差了。於是你就說“不謝了”,把口袋放回去,不再考慮它了。 無論口袋裡還有什麼東西,或許還有另一輛汽車的鑰匙,也沒有用了,因為你會得到那條爛魚。或許還有比爛魚更糟的東西(那麼你看著辦吧)。無論如何爛魚已經夠糟的了,而你知道挑那個有三明治的口袋肯定會更好。演算法 Alpha-Beta就是這麼工作的,並且只能用遞迴來實現。稍後我們再來談最小一方的策略,我希望這樣可以更明白些。 這個思想是在搜尋中傳遞兩個值,第一個值是Alpha,即搜尋到的最好值,任何比它更小的值就沒用了,因為策略就是知道Alpha的值,任何小於或等於Alpha的值都不會有所提高。 第二個值是Beta,即對於對手來說最壞的值。這是對手所能承受的最壞的結果,因為我們知道在對手看來,他總是會找到一個對策不比Beta更壞的。如果搜尋過程中返回Beta或比Beta更好的值,那就夠好的了,走棋的一方就沒有機會使用這種策略了。 在搜尋著法時,每個搜尋過的著法都返回跟Alpha和Beta有關的值,它們之間的關係非常重要,或許意味著搜尋可以停止並返回。 如果某個著法的結果小於或等於Alpha,那麼它就是很差的著法,因此可以拋棄。因為我前面說過,在這個策略中,局面對走棋的一方來說是以Alpha為評價的。 如果某個著法的結果大於或等於Beta,那麼整個結點就作廢了,因為對手不希望走到這個局面,而它有別的著法可以避免到達這個局面。因此如果我們找到的評價大於或等於Beta,就證明了這個結點是不會發生的,因此剩下的合理著法沒有必要再搜尋。 如果某個著法的結果大於Alpha但小於Beta,那麼這個著法就是走棋一方可以考慮走的,除非以後有所變化。因此Alpha會不斷增加以反映新的情況。有時候可能一個合理著法也不超過Alpha,這在實戰中是經常發生的,此時這種局面是不予考慮的,因此為了避免這樣的局面,我們必須在博弈樹的上一個層局面選擇另外一個著法。 在第二個口袋裡找到爛魚就相當於超過了Beta,如果口袋裡沒有爛魚,那麼考慮六盒裝流行唱片的口袋會比三明治的口袋好,這就相當於超過了Alpha(在上一層)。演算法如下,醒目的部分是在最小-最大演算法上改過的:int AlphaBeta(int depth, int alpha, int beta) { if (depth == 0) { return Evaluate(); } GenerateLegalMoves(); while (MovesLeft()) { MakeNextMove(); val = -AlphaBeta(depth - 1, -beta, -alpha); UnmakeMove(); if (val >= beta) { return beta; } if (val > alpha) { alpha = val; } } return alpha;} 把醒目的部分去掉,剩下的就是最小-最大函式。可以看出現在的演算法沒有太多的改變。 這個函式需要傳遞的引數有:需要搜尋的深度,負無窮大即Alpha,以及正無窮大即Beta:val = AlphaBeta(5, -INFINITY, INFINITY); 這樣就完成了5層的搜尋。我在寫最小-最大函式時,用了一個訣竅來避免用了“Min”還用“Max”函式。在那個演算法中,我從遞迴中返回時簡單地對返回值取了負數。這樣就使函式值在每一次遞迴中改變評價的角度,以反映雙方棋手的交替著子,並且它們的目標是對立的。 在Alpha-Beta函式中我們做了同樣的處理。唯一使演算法感到複雜的是,Alpha和Beta是不斷互換的。當函式遞迴時,Alpha和Beta不但取負數而且位置交換了,這就使得情況比口袋的例子複雜,但是可以證明它只是比最小-最大演算法更好而已。 最終出現的情況是,在搜尋樹的很多地方,Beta是很容易超過的,因此很多工作都免去了。可能的弱點 這個演算法嚴重依賴於著法的尋找順序。如果你總是先去搜索最壞的著法,那麼Beta截斷就不會發生,因此該演算法就如同最小-最大一樣,效率非常低。該演算法最終會找遍整個博弈樹,就像最小-最大演算法一樣。 如果程式總是能挑最好的著法來首先搜尋,那麼數學上有效分枝因子就接近於實際分枝因子的平方根。這是Alpha-Beta演算法可能達到的最好的情況。 由於國際象棋的分枝因子在35左右,這就意味著Alpha-Beta演算法能使國際象棋搜尋樹的分枝因子變成6。 這是很大的改進,在搜尋結點數一樣的情況下,可以使你的搜尋深度達到原來的兩倍。這就是為什麼使用Alpha-Beta搜尋時,著法順序至關重要的原因。 型別:全譯+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Alpha-Beta搜尋 David Eppstein */文 * 加州愛爾文大學(UC Irvine)資訊與計算機科學系 淺的裁剪 假設你用最小-最大搜索(前面講到的)來搜尋下面的樹: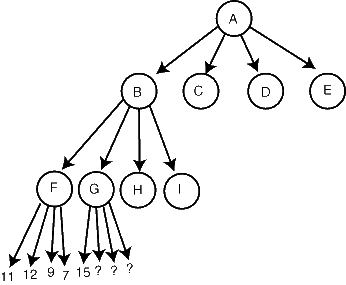 你搜索到F,發現子結點的評價分別是11、12、7和9,在這層是棋手甲走,我們希望他選擇最好的值,即12。所以,F的最小-最大值是12。 現在你開始搜尋G,並且第一個子結點就返回15。一旦如此,你就知道G的值至少是15,可能更高(如果另一個子結點比G更好)。這就意味著我們不指望棋手乙走G這步了,因為就棋手乙看來,F的評價12要比G的15(或更高)好,因此我們知道G不在主要變例上。我們可以裁剪(Prune)結點G下面的其他子結點,而不要對它們作出評價,並且立即從G返回,因為對G作更好的評價只是浪費時間。 一般來說,像G一樣只要有一個子結點返回比G的兄弟結點更好的值(對於結點G要走棋的一方而言),就可以進行裁剪。深的裁剪 我們來討論更復雜的可能裁剪的情況。例如在同一棵搜尋樹中,我們評價的G、H和I都比12好,因此12就是結點B的評價。現在我們來搜尋結點C,在下面兩層我們找到了評價為10的結點N:
你搜索到F,發現子結點的評價分別是11、12、7和9,在這層是棋手甲走,我們希望他選擇最好的值,即12。所以,F的最小-最大值是12。 現在你開始搜尋G,並且第一個子結點就返回15。一旦如此,你就知道G的值至少是15,可能更高(如果另一個子結點比G更好)。這就意味著我們不指望棋手乙走G這步了,因為就棋手乙看來,F的評價12要比G的15(或更高)好,因此我們知道G不在主要變例上。我們可以裁剪(Prune)結點G下面的其他子結點,而不要對它們作出評價,並且立即從G返回,因為對G作更好的評價只是浪費時間。 一般來說,像G一樣只要有一個子結點返回比G的兄弟結點更好的值(對於結點G要走棋的一方而言),就可以進行裁剪。深的裁剪 我們來討論更復雜的可能裁剪的情況。例如在同一棵搜尋樹中,我們評價的G、H和I都比12好,因此12就是結點B的評價。現在我們來搜尋結點C,在下面兩層我們找到了評價為10的結點N:
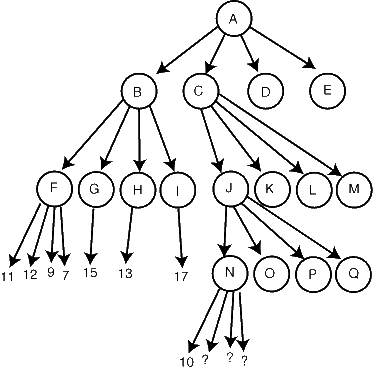 我們能用更為複雜的路線來作裁剪。我們知道N會返回10或更小(輪到棋手乙走棋,需要挑最小的)。我們不知道J能否返回10或更小,也不知道J的哪個子結點會更好。如果從J返回到C的是10或者更小的值,那麼我們可以在結點C上作裁剪,因為它有更好的兄弟結點B。因此在這種情況下,繼續找N的子結點就毫無意義。考慮其他情況,J的其他子結點返回比10更好的值,此時搜尋N也是毫無意義的。所以我們只要看到10,就可以放心地從N返回。Alpha-Beta的虛擬碼 一般來說,如果返回值比偶數層的兄弟結點好,我們就可以立即返回。如果我們在搜尋過程中,把這些兄弟結點的最小值Beta作為引數來傳遞,我們就可以進行非常有效的裁剪。我們還用另一個引數Alpha來儲存奇數層的結點。用這兩個引數來進行裁剪是非常有效的,程式碼就寫在下邊。像上次一樣,我們用負值最大(Negamax)的形式,即搜尋樹的層數改變時取負值。double alphabeta(int depth, double alpha, double beta) { if (depth <= 0 || 棋局結束) { return evaluation(); } 就當前局面,生成並排序一系列著法; for (每個著法 m) { 執行著法 m; double val = -alphabeta(depth - 1, -beta, -alpha); 撤消著法 m; if (val >= beta) { return val; } if (val > alpha) { alpha = val; } } return alpha;} 下次我們會解釋為什麼排序這一步是很重要的。期望搜尋 在根結點上我們如何為Alpha和Beta設定初值? Alpha和Beta定義了一個評價的實數區間(Alpha, Beta),這個區間是我們“感興趣的”。如果某值比Beta大我們就會做裁剪並立即返回,因為我們知道它不是主要變例的一部分,我們對它的準確值不感興趣,只需要知道它比Beta大。如果某值比Alpha小,我們不作裁剪,但是仍然對它不感興趣,因為我們知道搜尋樹裡肯定有一個著法會更好。 但是在搜尋樹的根結點,我們不知道感興趣的評價是在哪個範圍內,如果我們要保證不會因為意外而裁剪掉重要的部分,我們就設Alpha = -Infinity,Beta = Infinity(無窮大)。 但是,如果我們使用迭代加深,就可能有辦法知道主要變例是怎麼樣的。假設我們猜其值為x(例如x就是前一次搜尋到D -1深度時的值),並設Epsilon為一個很小的值,它代表從D -1深度到D深度搜索評價的期望變化範圍。我們可以嘗試呼叫alphabeta(D, x - Epsilon, x +
Epsilon),那麼可能發生三種情況: (1) 搜尋的返回值會落在區間(x - Epsilon, x + Epsilon)內。這種情況下,我們知道它返回的是正確值,我們就能放心地選擇這個著法,在搜尋樹中這個著法指向具有返回值的那個結點。 (2) 搜尋會返回一個值v > x + Epsilon。這種情況下,我們知道搜尋結果也至少是 x + Epsilon,但是我們不知道它到底是幾(正確的主要變例可能被裁剪掉了,因為我們看到有別的著法的值大於Beta)。我們必須把我們所猜的值x調整得更高,然後再試一次(可能還要用更大的Epsilon)。這種情況稱為“高出邊界”(Fail
High)。 (3) 搜尋會返回一個值v < x - Epsilon。這種情況下,我們知道搜尋結果也最多是 x + Epsilon,但是我們不知道它到底是幾。我們必須把我們所猜的值x調整得更低,然後再試一次(可能還要用更大的Epsilon)。這種情況稱為“低出邊界”(Fail Low)。 即便有兩種可能失敗的情況,使用期望搜尋(用一個比(-Infinity, Infinity)更小的區間(Alpha, Beta))總體來說效率會有所提高,因為它作了更多的裁剪。分析 讓我們對Alpha-Beta搜尋作一下分析,來知道它為什麼是個很有用的演算法。跟普通的演算法不同,我們採用“Beta情況的分析”,即假設任何可能的情況下都會發生Alpha-Beta裁剪。下一次我們會知道如何讓Alpha-Beta搜尋接近我們的所分析的情況。在這裡我只考慮淺的裁剪,因為它會讓分析變得更加簡單。 在最好的情況下,除了主要變例上的結點不會裁剪外(如果這個結點也被裁剪了,那麼整個演算法會高出邊界或低出邊界,這當然不是最好的情況),在裁剪前,深D -1層的每個結點只會搜尋一個深D層的子結點。 但是在深D -2層時,誰也沒有被裁剪,因為所有的子結點都返回大於或等於Beta的值,而D -2層是要取負數,因此它們都小於或等於Alpha。 繼續朝樹根走,D -3層的每個結點(除了主要變例外)都被裁剪,而D -4層誰也沒被裁剪,等等。 因此,如果搜尋樹的分枝因子是B,那麼在搜尋樹一半的深度上,結點以因子B作增長,而在另一半的深度上則保持不變(我們忽略了主要變例)。所以這個搜尋樹所有要搜尋的結點數,粗略地寫成BD/2 = sqrt(B)D。因此Alpha-Beta搜尋最終可以將分枝因子減少為原來的平方根那麼多,因此它可以讓我們搜尋原來兩倍的深度。正因為這個原因,它是所有基於最小-最大策略的棋類對弈程式的最重要的演算法。 【譯註:原作者一開始提到的“淺的裁剪”和“深的裁剪”這兩個概念,實際上包含了Alpha-Beta搜尋的兩個層次,前者只是用過傳遞引數Beta對搜尋樹作了部分裁剪,可以稱為Beta搜尋,而後者增加一個傳遞引數Alpha,使得裁剪更加充分,這就形成了Alpha-Beta搜尋。Beta搜尋的虛擬碼是:double alphabeta(int depth, double beta) { if (depth <= 0 || 棋局結束) { return evaluation(); } 就當前局面,生成並排序一系列著法; double alpha = -infty; for (每個著法 m) { 執行著法 m; double val = -alphabeta(depth - 1, -alpha); 撤消著法 m; if (val >= beta) { return val; } if (val > alpha) { alpha = val; } } return alpha;}對紅色部分加一些改進,就變成Alpha-Beta搜尋的虛擬碼了。】
我們能用更為複雜的路線來作裁剪。我們知道N會返回10或更小(輪到棋手乙走棋,需要挑最小的)。我們不知道J能否返回10或更小,也不知道J的哪個子結點會更好。如果從J返回到C的是10或者更小的值,那麼我們可以在結點C上作裁剪,因為它有更好的兄弟結點B。因此在這種情況下,繼續找N的子結點就毫無意義。考慮其他情況,J的其他子結點返回比10更好的值,此時搜尋N也是毫無意義的。所以我們只要看到10,就可以放心地從N返回。Alpha-Beta的虛擬碼 一般來說,如果返回值比偶數層的兄弟結點好,我們就可以立即返回。如果我們在搜尋過程中,把這些兄弟結點的最小值Beta作為引數來傳遞,我們就可以進行非常有效的裁剪。我們還用另一個引數Alpha來儲存奇數層的結點。用這兩個引數來進行裁剪是非常有效的,程式碼就寫在下邊。像上次一樣,我們用負值最大(Negamax)的形式,即搜尋樹的層數改變時取負值。double alphabeta(int depth, double alpha, double beta) { if (depth <= 0 || 棋局結束) { return evaluation(); } 就當前局面,生成並排序一系列著法; for (每個著法 m) { 執行著法 m; double val = -alphabeta(depth - 1, -beta, -alpha); 撤消著法 m; if (val >= beta) { return val; } if (val > alpha) { alpha = val; } } return alpha;} 下次我們會解釋為什麼排序這一步是很重要的。期望搜尋 在根結點上我們如何為Alpha和Beta設定初值? Alpha和Beta定義了一個評價的實數區間(Alpha, Beta),這個區間是我們“感興趣的”。如果某值比Beta大我們就會做裁剪並立即返回,因為我們知道它不是主要變例的一部分,我們對它的準確值不感興趣,只需要知道它比Beta大。如果某值比Alpha小,我們不作裁剪,但是仍然對它不感興趣,因為我們知道搜尋樹裡肯定有一個著法會更好。 但是在搜尋樹的根結點,我們不知道感興趣的評價是在哪個範圍內,如果我們要保證不會因為意外而裁剪掉重要的部分,我們就設Alpha = -Infinity,Beta = Infinity(無窮大)。 但是,如果我們使用迭代加深,就可能有辦法知道主要變例是怎麼樣的。假設我們猜其值為x(例如x就是前一次搜尋到D -1深度時的值),並設Epsilon為一個很小的值,它代表從D -1深度到D深度搜索評價的期望變化範圍。我們可以嘗試呼叫alphabeta(D, x - Epsilon, x +
Epsilon),那麼可能發生三種情況: (1) 搜尋的返回值會落在區間(x - Epsilon, x + Epsilon)內。這種情況下,我們知道它返回的是正確值,我們就能放心地選擇這個著法,在搜尋樹中這個著法指向具有返回值的那個結點。 (2) 搜尋會返回一個值v > x + Epsilon。這種情況下,我們知道搜尋結果也至少是 x + Epsilon,但是我們不知道它到底是幾(正確的主要變例可能被裁剪掉了,因為我們看到有別的著法的值大於Beta)。我們必須把我們所猜的值x調整得更高,然後再試一次(可能還要用更大的Epsilon)。這種情況稱為“高出邊界”(Fail
High)。 (3) 搜尋會返回一個值v < x - Epsilon。這種情況下,我們知道搜尋結果也最多是 x + Epsilon,但是我們不知道它到底是幾。我們必須把我們所猜的值x調整得更低,然後再試一次(可能還要用更大的Epsilon)。這種情況稱為“低出邊界”(Fail Low)。 即便有兩種可能失敗的情況,使用期望搜尋(用一個比(-Infinity, Infinity)更小的區間(Alpha, Beta))總體來說效率會有所提高,因為它作了更多的裁剪。分析 讓我們對Alpha-Beta搜尋作一下分析,來知道它為什麼是個很有用的演算法。跟普通的演算法不同,我們採用“Beta情況的分析”,即假設任何可能的情況下都會發生Alpha-Beta裁剪。下一次我們會知道如何讓Alpha-Beta搜尋接近我們的所分析的情況。在這裡我只考慮淺的裁剪,因為它會讓分析變得更加簡單。 在最好的情況下,除了主要變例上的結點不會裁剪外(如果這個結點也被裁剪了,那麼整個演算法會高出邊界或低出邊界,這當然不是最好的情況),在裁剪前,深D -1層的每個結點只會搜尋一個深D層的子結點。 但是在深D -2層時,誰也沒有被裁剪,因為所有的子結點都返回大於或等於Beta的值,而D -2層是要取負數,因此它們都小於或等於Alpha。 繼續朝樹根走,D -3層的每個結點(除了主要變例外)都被裁剪,而D -4層誰也沒被裁剪,等等。 因此,如果搜尋樹的分枝因子是B,那麼在搜尋樹一半的深度上,結點以因子B作增長,而在另一半的深度上則保持不變(我們忽略了主要變例)。所以這個搜尋樹所有要搜尋的結點數,粗略地寫成BD/2 = sqrt(B)D。因此Alpha-Beta搜尋最終可以將分枝因子減少為原來的平方根那麼多,因此它可以讓我們搜尋原來兩倍的深度。正因為這個原因,它是所有基於最小-最大策略的棋類對弈程式的最重要的演算法。 【譯註:原作者一開始提到的“淺的裁剪”和“深的裁剪”這兩個概念,實際上包含了Alpha-Beta搜尋的兩個層次,前者只是用過傳遞引數Beta對搜尋樹作了部分裁剪,可以稱為Beta搜尋,而後者增加一個傳遞引數Alpha,使得裁剪更加充分,這就形成了Alpha-Beta搜尋。Beta搜尋的虛擬碼是:double alphabeta(int depth, double beta) { if (depth <= 0 || 棋局結束) { return evaluation(); } 就當前局面,生成並排序一系列著法; double alpha = -infty; for (每個著法 m) { 執行著法 m; double val = -alphabeta(depth - 1, -alpha); 撤消著法 m; if (val >= beta) { return val; } if (val > alpha) { alpha = val; } } return alpha;}對紅色部分加一些改進,就變成Alpha-Beta搜尋的虛擬碼了。】
型別:全譯加譯註
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Alpha-Beta剪枝演算法(Alpha Beta Pruning)
Alpha-Beta剪枝用於裁剪搜尋樹中沒有意義的不需要搜尋的樹枝,以提高運算速度。
假設α為下界,β為上界,對於α ≤ N ≤ β:
若 α ≤ β 則N有解。
若 α > β 則N無解。
下面通過一個例子來說明Alpha-Beta剪枝演算法。

上圖為整顆搜尋樹。這裡使用極小極大演算法配合Alpha-Beta剪枝演算法,正方形為自己(A),圓為對手(B)。
初始設定α為負無窮大,β為正無窮大。

對於B(第四層)而已,儘量使得A獲利最小,因此當遇到使得A獲利更小的情況,則需要修改β。這裡3小於正無窮大,所以β修改為3。

(第四層)這裡17大於3,不用修改β。

對於A(第三層)而言,自己獲利越大越好,因此遇到利益值大於α的時候,需要α進行修改,這裡3大於負無窮大,所以α修改為3

B(第四層)擁有一個方案使得A獲利只有2,α=3, β=2, α > β, 說明A(第三層)只要選擇第二個方案, 則B必然可以使得A的獲利少於A(第三層)的第一個方案,這樣就不再需要考慮B(第四層)的其他候選方案了,因為A(第三層)根本不會選取第二個方案,多考慮也是浪費.

B(第二層)要使得A利益最小,則B(第二層)的第二個方案不能使得A的獲利大於β, 也就是3. 但是若B(第二層)選擇第二個方案, A(第三層)可以選擇第一個方案使得A獲利為15, α=15, β=3, α > β, 故不需要再考慮A(第三層)的第二個方案, 因為B(第二層)不會選擇第二個方案.

A(第一層)使自己利益最大,也就是A(第一層)的第二個方案不能差於第一個方案, 但是A(第三層)的一個方案會導致利益為2, 小於3, 所以A(第三層)不會選擇第一個方案, 因此B(第四層)也不用考慮第二個方案.

當A(第三層)考慮第二個方案時,發現獲得利益為3,和A(第一層)使用第一個方案利益一樣.如果根據上面的分析A(第一層)優先選擇了第一個方案,那麼B不再需要考慮第二種方案,如果A(第一層)還想進一步評估兩個方案的優劣的話, B(第二層)則還需要考慮第二個方案,若B(第二層)的第二個方案使得A獲利小於3,則A(第一層)只能選擇第一個方案,若B(第二層)的第二個方案使得A獲利大於3,則A(第一層)還需要根據其他因素來考慮最終選取哪種方案.
