郵箱:[email protected]
阿新 • • 發佈:2019-01-24
題意:
一些村莊被建立在一條筆直的高速公路邊上,我們用一條座標軸來描述這條高速公路,每一個村莊的座標都是整數,沒有兩個村莊座標相同。兩個村莊間的距離,定義為它們的座標值差的絕對值。我們需要在一些村莊建立郵局——當然,並不是每一個村莊都必須建立郵局,郵局必須被建立在村莊裡,因此它的座標和它所在的村莊座標相同。每個村莊使用離它最近的那個
郵局,建立這些郵局的原則是:所有村莊到各自所使用的郵局的距離總和最小。
你的任務是編寫一個程式,在給定了每個村莊座標和將要建立的郵局數之後,按照上述原則,合理地選擇這些郵局的位置。
求出的所有村莊到距離它最近的郵局的距離總和.
解析:
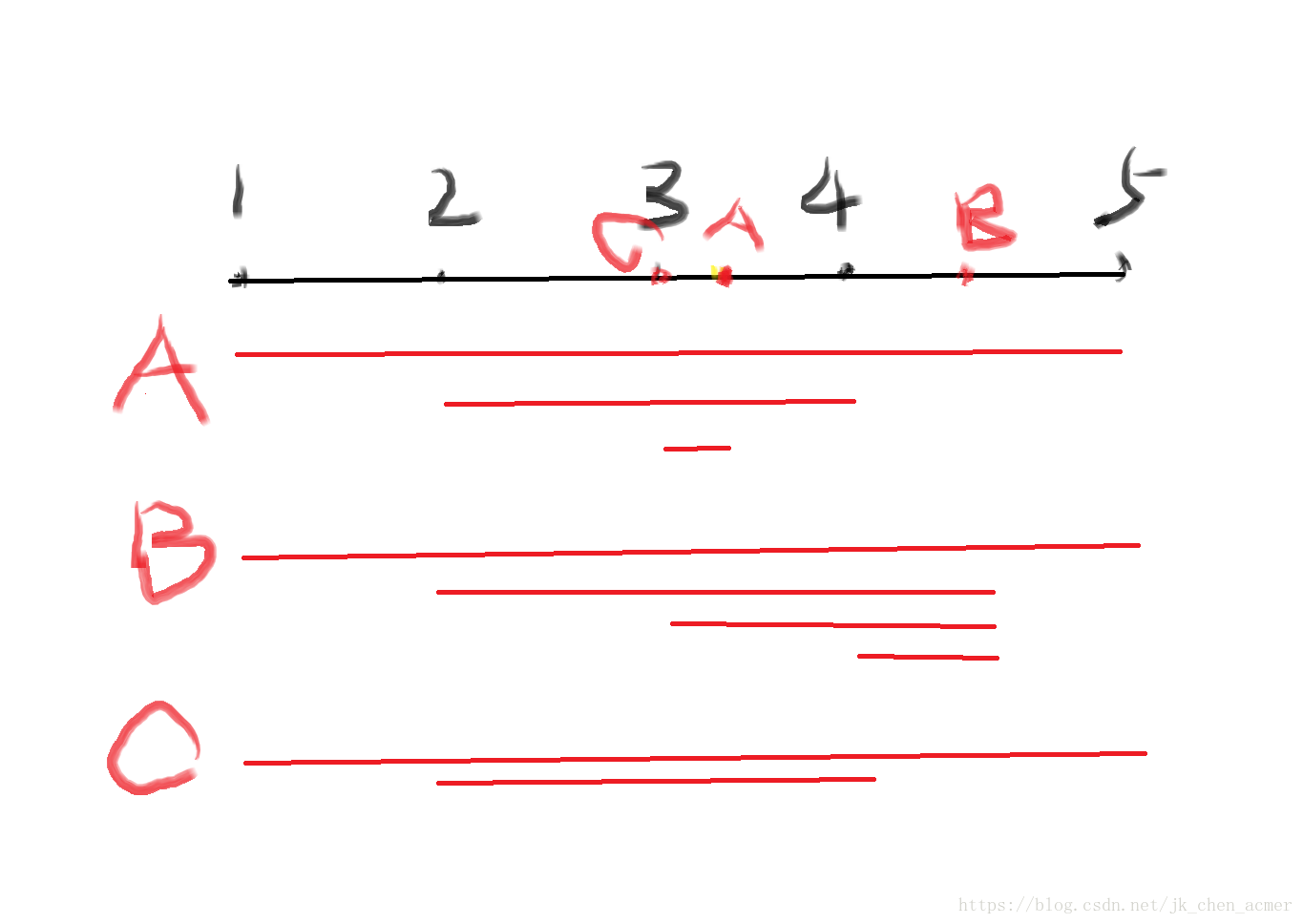
首先要知道點L到點R間放一個郵局的最短距離:
很明顯奇數個時當取最中間的那個點的時候最短(不是座標的中間,而是下標的中間),同理,偶數個時取中間兩個點之間的任何位置都可以。
對於這題我們需要預處理點L和點R之間建立一個郵局的最短距離和w[l][r],狀態轉移方程為w[l][r] = w[l][r-1]+a[r]-a[(r+l)>>1]
上圖解釋:
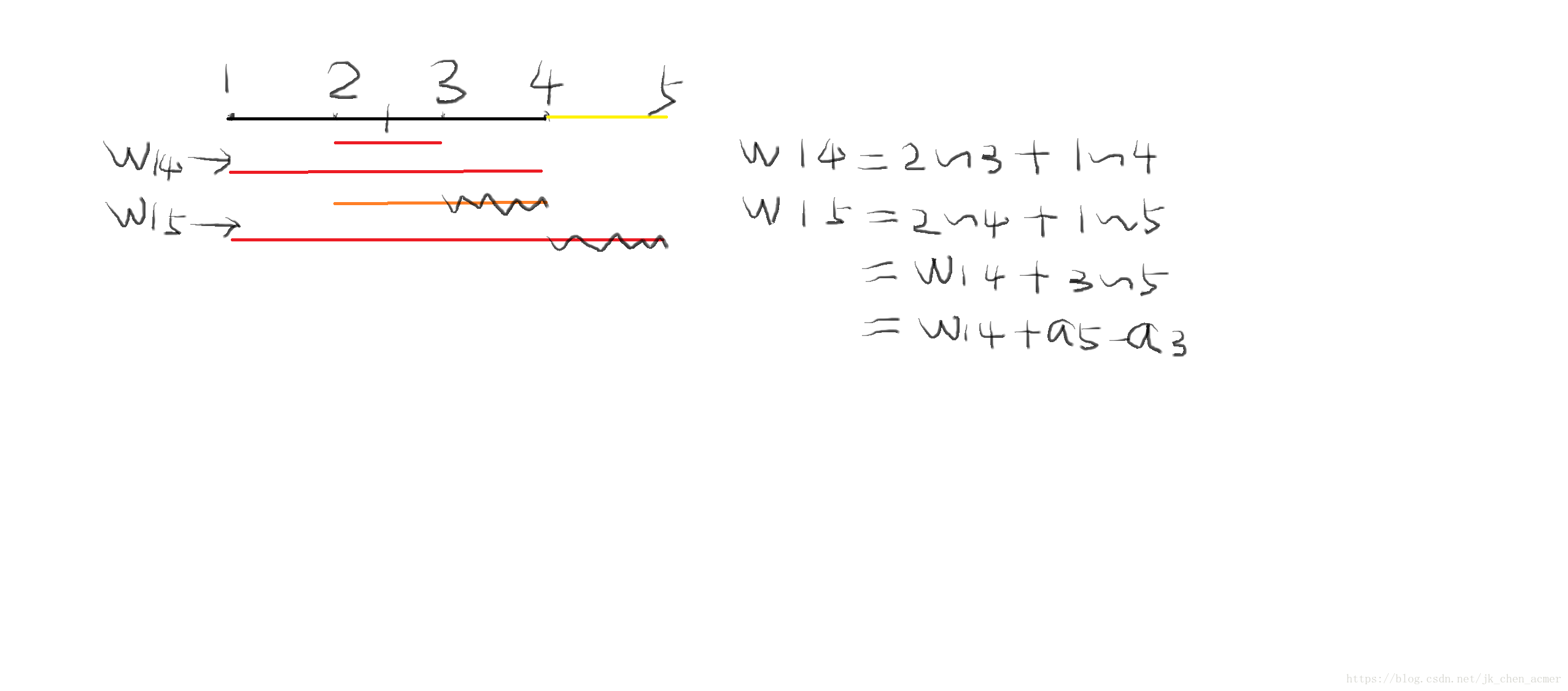
由前面講的知識可以得到1~5的距離和==1~4的距離和+a[5]-a[3],再畫一下1~6的==1~5的+a[6]-a[3],總結為w[l][r] = w[l][r-1]+a[r]-a[(r+l)>>1]
最後是dp陣列dp[i][j]代表從起點到i點間建立j個郵局的情況
是不是就有dp[i][j]=min(dp[i][j],dp[k][j-1]+w[k+1][i])
eg: dp[10][3]=dp[6][2]+w[7][10],1~10建3個郵局可以由1~6建2個郵局加上7~10建一個郵局轉化而來
程式碼:
#include<iostream>
#include<stdio.h>
#include<string.h>
using namespace std;
const int INF = ~0U>>1;
int a[309];
int dp[309][39];
int w[309][309];
int n,m;
int main(){
while(cin>>n>>m){
for