淺談LCA的線上演算法ST表
阿新 • • 發佈:2019-01-24
求LCA(最近公共祖先)的演算法有好多,按線上和離線分為線上演算法和離線演算法。
離線演算法有基於搜尋的Tarjan演算法比較好,而線上演算法則是基於dp的ST演算法比較好。
這次先講一下ST演算法。
這個演算法是基於RMQ(區間最大最小值編號)的,而求LCA就是把樹通過深搜得到一個序列,然後轉化為求區間的最小編號。
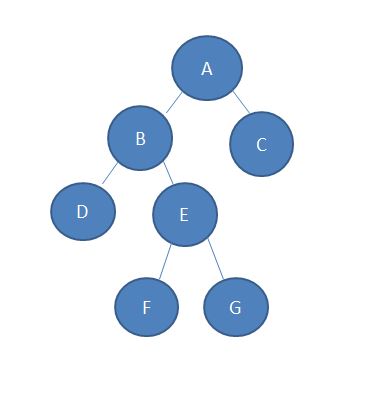
比如說給出這樣一棵樹。
通過深搜可以得到這樣一個序列:
節點ver: 1 2 1 3 4 3 5 6 5 7(左到右)
深度 R : 1 2 1 2 3 2 3 4 3 4
首位first:1 2 4 5 7 8 10 (即這個數第一次出現的位置)
或者這樣:
那麼就可以這樣寫深搜程式碼:
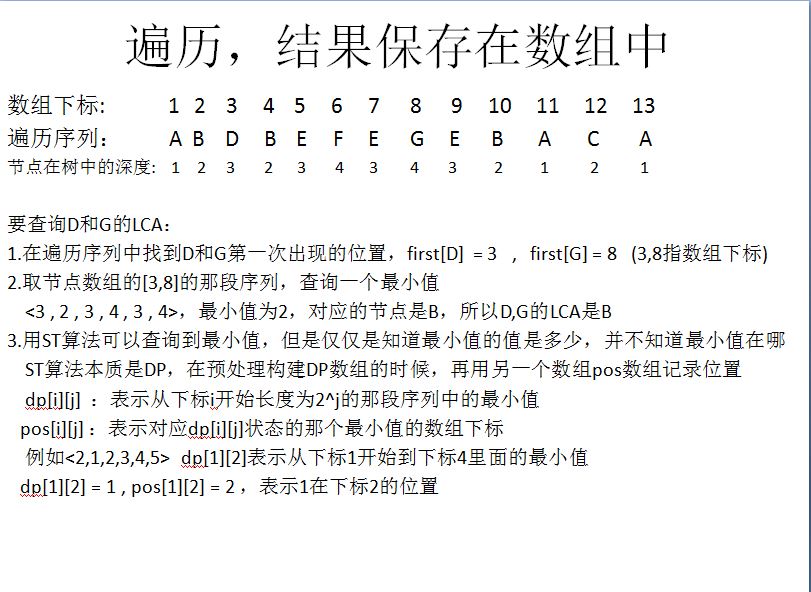
搜尋得到序列之後假如我們想求4 和7的 LCA。(最醜那幅圖。。。)int tot,head[N],ver[2*N],R[2*N],first[N],dir[N]; //ver:節點編號 R:深度 first:點編號第一次位置 dir:距離 void dfs(int u ,int dep) { vis[u] = true; ver[++tot] = u; first[u] = tot; R[tot] = dep; for(int k=head[u]; k!=-1; k=e[k].next) if( !vis[e[k].v] ) { int v = e[k].v , w = e[k].w; dir[v] = dir[u] + w; dfs(v,dep+1); //下面兩句表示dfs的時候還要回溯到上面 ver[++tot] = u; R[tot] = dep; } }
那麼我們找4和7在序列中的位置通過first 陣列查詢發現在5---10的ver陣列的範圍
即4 3 5 6 5 7 在上面圖上找發現正好是以3為根的子樹。而我們只要找到其中一個深度最小的編號即 3 就可以了。
這時候我們就用到了RMQ演算法。
維護一個dp陣列儲存其區間深度最小的下標,查詢的時候返回就可以了。
比如上面我們找到深度最小的為點3,返回其在ver陣列中的下標 6 即可。
程式碼可以這樣寫:
void ST(int n) { for(int i=1;i<=n;i++) dp[i][0] = i; for(int j=1;(1<<j)<=n;j++) { for(int i=1;i+(1<<j)-1<=n;i++) { int a = dp[i][j-1] , b = dp[i+(1<<(j-1))][j-1]; dp[i][j] = R[a]<R[b]?a:b; } } } //中間部分是交叉的。 int RMQ(int l,int r) { int k=0; while((1<<(k+1))<=r-l+1) k++; int a = dp[l][k], b = dp[r-(1<<k)+1][k]; //儲存的是編號 return R[a]<R[b]?a:b; } int LCA(int u ,int v) { int x = first[u] , y = first[v]; if(x > y) swap(x,y); int res = RMQ(x,y); return ver[res]; }