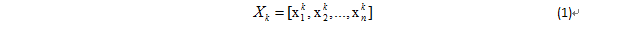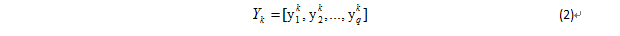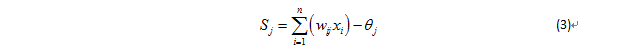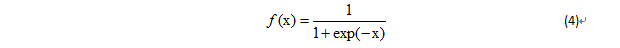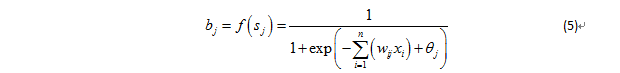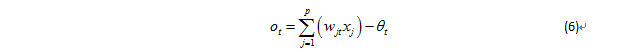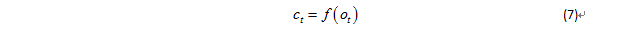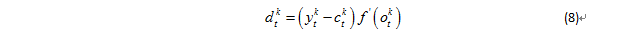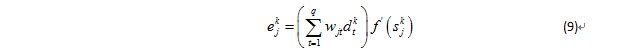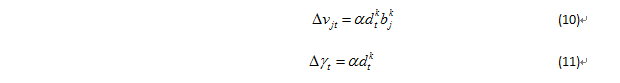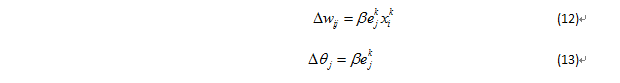BP神經網絡公式推導及實現 MNIST

阿新 • • 發佈：2019-01-24

result protect 包括狀態集合 bp算法 print rate error

BP神經網絡的基礎介紹見：http://blog.csdn.net/fengbingchun/article/details/50274471，這裏主要以公式推導為主。

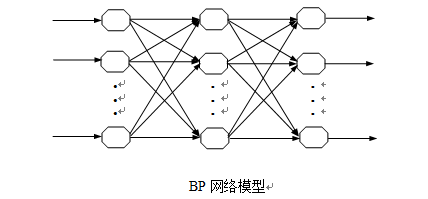
BP神經網絡又稱為誤差反向傳播網絡，其結構如下圖。這種網絡實質是一種前向無反饋網絡，具有結構清晰、易實現、計算功能強大等特點。

技術分享圖片

BP神經網絡有一個輸入層，一個輸出層，一個或多個隱含層。每一層上包含了若幹個節點，每個節點代表一個神經元，同一層上各節點之間無任何耦合連接關系，層間各神經元之間實現全連接，即後一層(如輸入層)的每一個神經元與前一層(如隱含層)的每一個神經元實現全連接。網絡按照監督學習的方式學習，當信息被輸入網絡後神經元受到刺激，激活值從輸入層依次經過各隱含層節點，最後在輸出層的各節點獲得網絡的輸入響應。

BP神經網絡的基本思想：BP神經網絡的學習采用誤差反向傳播算法，BP算法是一種有監督的學習方法，其主要思想是把整個學習過程分為正向傳播、反向(逆向)傳播和記憶訓練三個部分。正向傳播時，輸入樣本從輸入層輸入，經各隱含層處理後傳向輸出層，每一層神經元的狀態只影響下一層神經元的狀態。如果在輸出層得不到期望的輸出，則轉入誤差的反向傳播階段，將輸出誤差以某種形式通過隱含層向輸入層反傳，並將誤差分攤給各層的所有單元，從而獲得各層單元的誤差信號並將其作為修正各單元權值的依據。這種網絡的信號正向傳播與誤差反向傳播是反復交替進行的，權值的不斷調整就是網絡的記憶訓練過程。網絡的記憶訓練過程一直進行到網絡趨向收斂，即輸出誤差達到要求的標準。

三層BP神經網絡的學習算法：為了使BP網絡具有某種功能，完成某項任務，必須調整層間連接權值和節點閾值，使所有樣品的實際輸出和期望輸出之間的誤差穩定在一個較小的值之內。三層BP網絡學習過程主要由四部分組成：(1)、輸入模式順傳播(輸入模式由輸入層經隱含層向輸出層傳播計算)；(2)、輸出誤差逆傳播(輸出的誤差由輸出層經隱含層傳向輸入層)；(3)、循環記憶訓練(模式順傳播與誤差逆傳播的計算過程反復交替循環進行)；(4)、學習結果判別(判定全局誤差是否趨向極小值或是否已達到設定的最大叠代次數)。

(1)、輸入模式順傳播：這一過程主要是利用輸入模式求出它所對應的實際輸出。

確定輸入向量X_k：

技術分享圖片

式中，k=1,2,…,m；m是學習模式對數(訓練模式對數)；n是輸入層單元數。

確定期望輸出向量Y_k：

技術分享圖片

式中，k=1,2,…,m；m是學習模式對數(訓練模式對數)；q為輸出層單元數。

計算隱含層各神經元的激活值s_j：

技術分享圖片

式中，n是輸入層單元數；w_ij是輸入層至隱含層的連接權值；θ_j是隱含層單元的閾值；j=1,2…p，p是隱含層單元數。

激活函數采用s型函數：

技術分享圖片

計算隱含層j單元的輸出值：將上面的激活值即公式(3)代入激活函數即公式(4)中可得隱含層j單元的輸出值：

技術分享圖片

閾值θ_j在學習過程中與權值w_ij一樣也不斷地被修正。

計算輸出層第t個單元的激活值o_t：

技術分享圖片

計算輸出層第t個單元的實際輸出值c_t：

技術分享圖片

式中，w_jt是隱含層至輸出層的權值；θ_t是輸出層單元閾值；j=1,2…p，p是隱含層單元數；x_j為隱含層第j個節點的輸出值；f是s型激活函數，t=1,2…,q，q為輸出層單元數。

利用以上各公式就可以計算出一個輸入模式的順傳播過程。

(2)、輸出誤差的逆傳播：在第一步的模式順傳播計算中得到了網絡的實際輸出值，當這些實際的輸出值與希望的輸出值不一樣或者誤差大於所限定的數值時，就要對網絡進行校正。

這裏的校正是從前往後進行的，所以叫做誤差逆傳播，計算時是從輸出層到隱含層，再從隱含層到輸入層。

輸出層的校正誤差：

技術分享圖片

式中，t=1,2,…,q，q是輸出層單元數；k=1,2,…,m，m是訓練(學習)模式對數；y_t^k是希望輸出；c_t^k是實際輸出；f^’(.)是對輸出函數的導數。

隱含層各單元的校正誤差：

技術分享圖片

式中，t=1,2,…,q，q是輸出層單元數；j=1,2,…,p; p是隱含層單元數；k=1,2,…,m，m是訓練(學習)模式對數。

對於輸出層至隱含層連接權和輸出層閾值的校正量：

技術分享圖片

式中，b_j^k是隱含層j單元的輸出；d_t^k是輸出層的校正誤差；j=1,2…,p；t=1,2,…,q；k=1,2,…,m； α>0(輸出層至隱含層學習率)。

隱含層至輸入層的校正量：

技術分享圖片

式中，e_j^k是隱含層j單元的校正誤差；x_i^k是標準輸入，i=1,2,…,n ，n是輸入層單元數；0<β<1(隱含層至輸入層學習率)。

(3)、循環記憶訓練：為使網絡的輸出誤差趨向於極小值，對於BP網輸入的每一組訓練模式，一般要經過數百次甚至上萬次的循環記憶訓練，才能使網絡記住這一模式。這種循環記憶實際上就是反復重復上面介紹的輸入模式順傳播和輸出誤差逆傳播。

(4)、學習結果的判別：當每次循環記憶訓練結束後，都要進行學習結果的判別。判別的目的主要是檢查輸出誤差是否已經小到可以允許的程度。如果小到可以允許的程度，就可以結束整個學習過程，否則還要繼續進行循環訓練。

確定隱含層節點數：一般有3個經驗公式：

技術分享圖片

式中，m為要設置的隱含層節點數；n為輸入層節點數；l為輸出層節點數；α為1至10之間的常數。

以下按照上面的公式實現的BP，通過MNIST庫測試，識別率可以達到96.5%以上。

BP.hpp:

#ifndef _BP_HPP_
#define _BP_HPP_

namespace ANN {

#define num_node_input_BP	784 //輸入層節點數
#define width_image_BP		28 //歸一化圖像寬
#define height_image_BP		28 //歸一化圖像高
#define num_node_hidden_BP	120 //隱含層節點數
#define num_node_output_BP	10 //輸出層節點數
#define alpha_learning_BP	0.8 //輸出層至隱含層學習率
#define beta_learning_BP	0.6 //隱含層至輸入層學習率
#define patterns_train_BP	60000 //訓練模式對數(總數)
#define patterns_test_BP	10000 //測試模式對數(總數)
#define iterations_BP		10000 //最大訓練次數
#define accuracy_rate_BP	0.965 //要求達到的準確率

class BP {
public:
	BP();
	~BP();

	void init(); //初始化，分配空間
	bool train(); //訓練
	int predict(const int* data, int width, int height); //預測
	bool readModelFile(const char* name); //讀取已訓練好的BP model

protected:
	void release(); //釋放申請的空間
	bool saveModelFile(const char* name); //將訓練好的model保存起來，包括各層的節點數，權值和閾值
	bool initWeightThreshold(); //初始化，產生[-1, 1]之間的隨機小數
	bool getSrcData(); //讀取MNIST數據
	void calcHiddenLayer(const int* data); //計算隱含層輸出
	void calcOutputLayer(); //計算輸出層輸出
	void calcAdjuctOutputLayer(const int* data); //計算輸出層校正誤差
	void calcAdjuctHiddenLayer(); //計算隱含層校正誤差
	float calcActivationFunction(float x); //計算激活函數，對數S形函數
	void updateWeightThresholdOutputLayer(); //更新輸出層至隱含層權值和閾值
	void updateWeightThresholdHiddenLayer(const int* data); //更新隱含層至輸入層權值和閾值
	float test(); //訓練完一次計算一次準確率

private:
	float weight1[num_node_input_BP][num_node_hidden_BP]; //輸入層至隱含層連接權值
	float weight2[num_node_hidden_BP][num_node_output_BP]; //隱含層至輸出層連接權值
	float threshold1[num_node_hidden_BP]; //隱含層閾值
	float threshold2[num_node_output_BP]; //輸出層閾值
	float output_hiddenLayer[num_node_hidden_BP]; //順傳播，隱含層輸出值
	float output_outputLayer[num_node_output_BP]; //順傳播，輸出層輸出值
	float adjust_error_outputLayer[num_node_output_BP]; //逆傳播，輸出層校正誤差
	float adjust_error_hiddenLayer[num_node_hidden_BP]; //逆傳播，隱含層校正誤差

	int* data_input_train; //原始標準輸入數據，訓練
	int* data_output_train; //原始標準期望結果，訓練
	int* data_input_test; //原始標準輸入數據，測試
	int* data_output_test; //原始標準期望結果，測試
};

}

#endif //_BP_HPP_

BP.cpp:

#include <assert.h>
#include <time.h>
#include <iostream>
#include <fstream>
#include <algorithm>
#include <windows.h>

#include "BP.hpp"

namespace ANN {

BP::BP()
{
	data_input_train = NULL;
	data_output_train = NULL;
	data_input_test = NULL;
	data_output_test = NULL;
}

BP::~BP()
{
	release();
}

void BP::release()
{
	if (data_input_train) {
		delete[] data_input_train;
	}
	if (data_output_train) {
		delete[] data_output_train;
	}
	if (data_input_test) {
		delete[] data_input_test;
	}
	if (data_output_test) {
		delete[] data_output_test;
	}
}

bool BP::initWeightThreshold()
{
	srand(time(0) + rand());

	for (int i = 0; i < num_node_input_BP; i++) {
		for (int j = 0; j < num_node_hidden_BP; j++) {
			weight1[i][j] = -1 + 2 * ((float)rand()) / RAND_MAX; //[-1, 1]
		}
	}

	for (int i = 0; i < num_node_hidden_BP; i++) {
		for (int j = 0; j < num_node_output_BP; j++) {
			weight2[i][j] = -1 + 2 * ((float)rand()) / RAND_MAX;
		}
	}

	for (int i = 0; i < num_node_hidden_BP; i++) {
		threshold1[i] = -1 + 2 * ((float)rand()) / RAND_MAX;
	}

	for (int i = 0; i < num_node_output_BP; i++) {
		threshold2[i] = -1 + 2 * ((float)rand()) / RAND_MAX;
	}

	return true;
}

static int reverseInt(int i)
{
	unsigned char ch1, ch2, ch3, ch4;
	ch1 = i & 255;
	ch2 = (i >> 8) & 255;
	ch3 = (i >> 16) & 255;
	ch4 = (i >> 24) & 255;
	return((int)ch1 << 24) + ((int)ch2 << 16) + ((int)ch3 << 8) + ch4;
}

static void readMnistImages(std::string filename, int* data_dst, int num_image)
{
	std::ifstream file(filename, std::ios::binary);
	assert(file.is_open());

	int magic_number = 0;
	int number_of_images = 0;
	int n_rows = 0;
	int n_cols = 0;
	file.read((char*)&magic_number, sizeof(magic_number));
	magic_number = reverseInt(magic_number);
	file.read((char*)&number_of_images, sizeof(number_of_images));
	number_of_images = reverseInt(number_of_images);
	assert(number_of_images == num_image);
	file.read((char*)&n_rows, sizeof(n_rows));
	n_rows = reverseInt(n_rows);
	file.read((char*)&n_cols, sizeof(n_cols));
	n_cols = reverseInt(n_cols);
	assert(n_rows == height_image_BP && n_cols == width_image_BP);

	for (int i = 0; i < number_of_images; ++i) {
		for (int r = 0; r < n_rows; ++r) {
			for (int c = 0; c < n_cols; ++c) {
				unsigned char temp = 0;
				file.read((char*)&temp, sizeof(temp));
				//data_dst[i * num_node_input_BP + r * n_cols + c] = (int)temp; //formula[1]
				if (temp > 128) {
					data_dst[i * num_node_input_BP + r * n_cols + c] = 1;
				} else {
					data_dst[i * num_node_input_BP + r * n_cols + c] = 0;
				}
			}
		}
	}
}

static void readMnistLabels(std::string filename, int* data_dst, int num_image)
{
	std::ifstream file(filename, std::ios::binary);
	assert(file.is_open());

	int magic_number = 0;
	int number_of_images = 0;
	file.read((char*)&magic_number, sizeof(magic_number));
	magic_number = reverseInt(magic_number);
	file.read((char*)&number_of_images, sizeof(number_of_images));
	number_of_images = reverseInt(number_of_images);
	assert(number_of_images == num_image);

	for (int i = 0; i < number_of_images; ++i) {
		unsigned char temp = 0;
		file.read((char*)&temp, sizeof(temp));
		data_dst[i * num_node_output_BP + temp] = 1; //formula[2]
	}
}

bool BP::getSrcData()
{
	assert(data_input_train && data_output_train && data_input_test && data_output_test);

	std::string filename_train_images = "D:/Download/MNIST/train-images.idx3-ubyte";
	std::string filename_train_labels = "D:/Download/MNIST/train-labels.idx1-ubyte";
	readMnistImages(filename_train_images, data_input_train, patterns_train_BP);
	/*unsigned char* p = new unsigned char[784];
	memset(p, 0, sizeof(unsigned char) * 784);
	for (int j = 0, i = 59998 * 784; j< 784; j++, i++) {
		p[j] = (unsigned char)data_input_train[i];
	}
	delete[] p;*/
	readMnistLabels(filename_train_labels, data_output_train, patterns_train_BP);
	/*int* q = new int[10];
	memset(q, 0, sizeof(int) * 10);
	for (int j = 0, i = 59998 * 10; j < 10; j++, i++) {
		q[j] = data_output_train[i];
	}
	delete[] q;*/

	std::string filename_test_images = "D:/Download/MNIST/t10k-images.idx3-ubyte";
	std::string filename_test_labels = "D:/Download/MNIST/t10k-labels.idx1-ubyte";
	readMnistImages(filename_test_images, data_input_test, patterns_test_BP);
	readMnistLabels(filename_test_labels, data_output_test, patterns_test_BP);

	return true;
}

void BP::init()
{
	data_input_train = new int[patterns_train_BP * num_node_input_BP];
	memset(data_input_train, 0, sizeof(int) * patterns_train_BP * num_node_input_BP);
	data_output_train = new int[patterns_train_BP * num_node_output_BP];
	memset(data_output_train, 0, sizeof(int) * patterns_train_BP * num_node_output_BP);
	data_input_test = new int[patterns_test_BP * num_node_input_BP];
	memset(data_input_test, 0, sizeof(int) * patterns_test_BP * num_node_input_BP);
	data_output_test = new int[patterns_test_BP * num_node_output_BP];
	memset(data_output_test, 0, sizeof(int) * patterns_test_BP * num_node_output_BP);

	initWeightThreshold();
	getSrcData();
}

float BP::calcActivationFunction(float x)
{
	return 1.0 / (1.0 + exp(-x)); //formula[4] formula[5] formula[7]
}

void BP::calcHiddenLayer(const int* data)
{
	for (int i = 0; i < num_node_hidden_BP; i++) {
		float tmp = 0;
		for (int j = 0; j < num_node_input_BP; j++) {
			tmp += data[j] * weight1[j][i];
		}

		tmp -= threshold1[i]; //formula[3]
		output_hiddenLayer[i] = calcActivationFunction(tmp);
	}
}

void BP::calcOutputLayer()
{
	for (int i = 0; i < num_node_output_BP; i++) {
		float tmp = 0;
		for (int j = 0; j < num_node_hidden_BP; j++) {
			tmp += output_hiddenLayer[j] * weight2[j][i];
		}

		tmp -= threshold2[i]; //formula[6]
		output_outputLayer[i] = calcActivationFunction(tmp);
	}
}

void BP::calcAdjuctOutputLayer(const int* data)
{
	for (int i = 0; i < num_node_output_BP; i++) {
		adjust_error_outputLayer[i] = (data[i] - output_outputLayer[i]) *
			output_outputLayer[i] * (1.0 - output_outputLayer[i]); //formula[8], f‘(x)= f(x)*(1. - f(x))
	}
}

void BP::calcAdjuctHiddenLayer()
{
	for (int i = 0; i < num_node_hidden_BP; i++) {
		float tmp = 0;
		for (int j = 0; j < num_node_output_BP; j++) {
			tmp += weight2[i][j] * adjust_error_outputLayer[j];
		}

		adjust_error_hiddenLayer[i] = tmp * (output_hiddenLayer[i] * (1.0 - output_hiddenLayer[i])); //formula[9]
	}
}

void BP::updateWeightThresholdOutputLayer()
{
	for (int i = 0; i < num_node_output_BP; i++) {
		for (int j = 0; j < num_node_hidden_BP; j++) {
			weight2[j][i] += (alpha_learning_BP * adjust_error_outputLayer[i] * output_hiddenLayer[j]); //formula[10]
		}

		threshold2[i] += (alpha_learning_BP * adjust_error_outputLayer[i]); //formula[11]
	}
}

void BP::updateWeightThresholdHiddenLayer(const int* data)
{
	for (int i = 0; i < num_node_hidden_BP; i++) {
		for (int j = 0; j < num_node_input_BP; j++) {
			weight1[j][i] += (beta_learning_BP * adjust_error_hiddenLayer[i] * data[j]); //formula[12]
		}

		threshold1[i] += (beta_learning_BP * adjust_error_hiddenLayer[i]); //formula[13]
	}
}

float BP::test()
{
	int count_accuracy = 0;

	for (int num = 0; num < patterns_test_BP; num++) {
		int* p1 = data_input_test + num * num_node_input_BP;
		calcHiddenLayer(p1);
		calcOutputLayer();

		float max_value = -9999;
		int pos = -1;

		for (int i = 0; i < num_node_output_BP; i++) {
			if (output_outputLayer[i] > max_value) {
				max_value = output_outputLayer[i];
				pos = i;
			}
		}

		int* p2 = data_output_test + num * num_node_output_BP;
		if (p2[pos] == 1) {
			count_accuracy++;
		}
		Sleep(1);
	}

	return (count_accuracy * 1.0 / patterns_test_BP);
}

bool BP::saveModelFile(const char* name)
{
	FILE* fp = fopen(name, "wb");
	if (fp == NULL) {
		return false;
	}

	int num_node_input = num_node_input_BP;
	int num_node_hidden = num_node_hidden_BP;
	int num_node_output = num_node_output_BP;
	fwrite(&num_node_input, sizeof(int), 1, fp);
	fwrite(&num_node_hidden, sizeof(int), 1, fp);
	fwrite(&num_node_output, sizeof(int), 1, fp);
	fwrite(weight1, sizeof(weight1), 1, fp);
	fwrite(threshold1, sizeof(threshold1), 1, fp);
	fwrite(weight2, sizeof(weight2), 1, fp);
	fwrite(threshold2, sizeof(threshold2), 1, fp);

	fflush(fp);
	fclose(fp);

	return true;
}

bool BP::readModelFile(const char* name)
{
	FILE* fp = fopen(name, "rb");
	if (fp == NULL) {
		return false;
	}

	int num_node_input, num_node_hidden, num_node_output;

	fread(&num_node_input, sizeof(int), 1, fp);
	assert(num_node_input == num_node_input_BP);
	fread(&num_node_hidden, sizeof(int), 1, fp);
	assert(num_node_hidden == num_node_hidden_BP);
	fread(&num_node_output, sizeof(int), 1, fp);
	assert(num_node_output == num_node_output_BP);
	fread(weight1, sizeof(weight1), 1, fp);
	fread(threshold1, sizeof(threshold1), 1, fp);
	fread(weight2, sizeof(weight2), 1, fp);
	fread(threshold2, sizeof(threshold2), 1, fp);

	fflush(fp);
	fclose(fp);

	return true;
}

int BP::predict(const int* data, int width, int height)
{
	assert(data && width == width_image_BP && height == height_image_BP);

	const int* p = data;
	calcHiddenLayer(p);
	calcOutputLayer();

	float max_value = -9999;
	int ret = -1;

	for (int i = 0; i < num_node_output_BP; i++) {
		if (output_outputLayer[i] > max_value) {
			max_value = output_outputLayer[i];
			ret = i;
		}
	}

	return ret;
}

bool BP::train()
{
	int i = 0;
	for (i = 0; i < iterations_BP; i++) {
		std::cout << "iterations : " << i;

		float accuracyRate = test();
		std::cout << ",    accuray rate: " << accuracyRate << std::endl;
		if (accuracyRate > accuracy_rate_BP) {
			saveModelFile("bp.model");
			std::cout << "generate bp model" << std::endl;
			break;
		}

		for (int j = 0; j < patterns_train_BP; j++) {
			int* p1 = data_input_train + j * num_node_input_BP;
			calcHiddenLayer(p1);
			calcOutputLayer();

			int* p2 = data_output_train + j * num_node_output_BP;
			calcAdjuctOutputLayer(p2);
			calcAdjuctHiddenLayer();

			updateWeightThresholdOutputLayer();
			int* p3 = data_input_train + j * num_node_input_BP;
			updateWeightThresholdHiddenLayer(p3);
		}
	}

	if (i == iterations_BP) {
		saveModelFile("bp.model");
		std::cout << "generate bp model" << std::endl;
	}

	return true;
}

}

test.cpp:

#include <iostream>
#include "BP.hpp"
#include <opencv2/opencv.hpp>

int test_BP();

int main()
{
	test_BP();
	std::cout << "ok!" << std::endl;
}

int test_BP()
{
	//1. bp train
	ANN::BP bp1;
	bp1.init();
	bp1.train();

	//2. bp predict
	ANN::BP bp2;
	bool flag = bp2.readModelFile("bp.model");
	if (!flag) {
		std::cout << "read bp model error" << std::endl;
		return -1;
	}

	int target[10] = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 };
	std::string path_images = "../../../../test-images/";

	int* data_image = new int[width_image_BP * height_image_BP];

	for (int i = 0; i < 10; i++) {
		char ch[15];
		sprintf(ch, "%d", i);
		std::string str;
		str = std::string(ch);
		str += ".jpg";
		str = path_images + str;

		cv::Mat mat = cv::imread(str, 2 | 4);
		if (!mat.data) {
			std::cout << "read image error" << std::endl;
			return -1;
		}

		if (mat.channels() == 3) {
			cv::cvtColor(mat, mat, cv::COLOR_BGR2GRAY);
		}

		if (mat.cols != width_image_BP || mat.rows != height_image_BP) {
			cv::resize(mat, mat, cv::Size(width_image_BP, height_image_BP));
		}

		memset(data_image, 0, sizeof(int) * (width_image_BP * height_image_BP));

		for (int h = 0; h < mat.rows; h++) {
			uchar* p = mat.ptr(h);
			for (int w = 0; w < mat.cols; w++) {
				if (p[w] > 128) {
					data_image[h* mat.cols + w] = 1;
				}
			}
		}

		int ret = bp2.predict(data_image, mat.cols, mat.rows);
		std::cout << "correct result: " << i << ",    actual result: " << ret << std::endl;
	}

	delete[] data_image;

	return 0;
}

train結果如下圖所示：

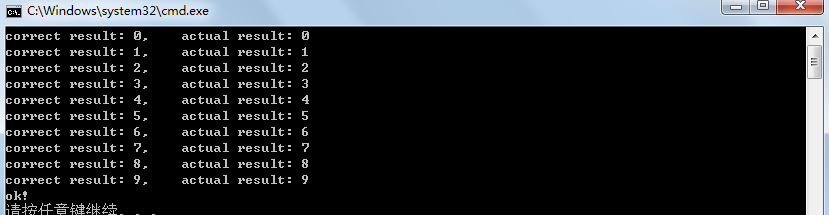
predict結果如下圖所示，測試圖像是從MNIST test集合中選取的：

技術分享圖片

GitHub：https://github.com/fengbingchun/NN

再分享一下我老師大神的人工智能教程吧。零基礎！通俗易懂！風趣幽默！還帶黃段子！希望你也加入到我們人工智能的隊伍中來！https://blog.csdn.net/jiangjunshow

BP神經網絡公式推導及實現 MNIST

result protect 包括狀態集合 bp算法 print rate error BP神經網絡的基礎介紹見：http://blog.csdn.net/fengbingchun/article/details/50274471，這裏主要以公式推導為主。 BP神經網

BP神經網絡公式推導及實現 MNIST

BP神經網絡公式推導及實現 MNIST

bp神經網絡模型推導與c語言實現（轉載）

BP神經網絡（原理及MATLAB實現）

詳細MATLAB 中BP神經網絡算法的實現

bp神經網絡的實現C++

Javascript實現BP神經網絡

logistic邏輯迴歸公式推導及R語言實現

最小二乘法擬合圓公式推導及vc實現[r]

二維空間點到直線垂足計算公式推導及Java實現——學習筆記

感知器和神經網路訓練（公式推導及C++實現）

Python實現——二層BP神經網絡

邏輯迴歸(Logistic Regression)詳解,公式推導及程式碼實現

BP神經網絡（手寫數字識別）

BP神經網絡

為什麽說BP神經網絡就是人工神經網絡的一種？

最簡單的神經網絡-感知器-python實現

Matlab-bp神經網絡

python構建bp神經網絡_鳶尾花分類(一個隱藏層)__1.數據集

KVM虛擬化的四種簡單網絡模型介紹及實現（一）

KVM虛擬化的四種簡單網絡模型介紹及實現（二）

BP神經網絡公式推導及實現 MNIST

相關推薦