Logistic邏輯迴歸

Logistic邏輯迴歸模型

線性迴歸模型簡單，對於一些線性可分的場景還是簡單易用的。Logistic邏輯迴歸也可以看成線性迴歸的變種，雖然名字帶回歸二字但實際上他主要用來二分類，區別於線性迴歸直接擬合目標值，Logistic邏輯迴歸擬合的是正類和負類的對數機率。

假設有一個二分類問題，輸出為y∈{0,1}

定義sigmoid函式:

用sigmoid函式的輸出是0，1之間，用來擬合y=1的概率，其函式R語言畫圖如下：

x = seq(-5, 5, 0.1)
y = 1 / (1 + exp(-1*x))
plot(x, y, type="line")

logistic邏輯迴歸可以擬合因變數為1的概率,最終分類的時候，我們可以一個閾值，比如0.5，大於閾值的都分為正類，向量化公式如下：

還可以換一種方式理解logistic邏輯迴歸，他是用多元線性函式去擬合因變數為正例與反例的比值的自然對數，推導如下：

Logistic邏輯迴歸演算法

• 假設自變數維度為N
• W為自變數的係數，下標0 - N
• X為自變數向量或矩陣，X維度為N,為了能和W0對應，X需要在第一行插入一個全是1的列。
• Y為因變數
• W為未知數待求解

最大似然估計法

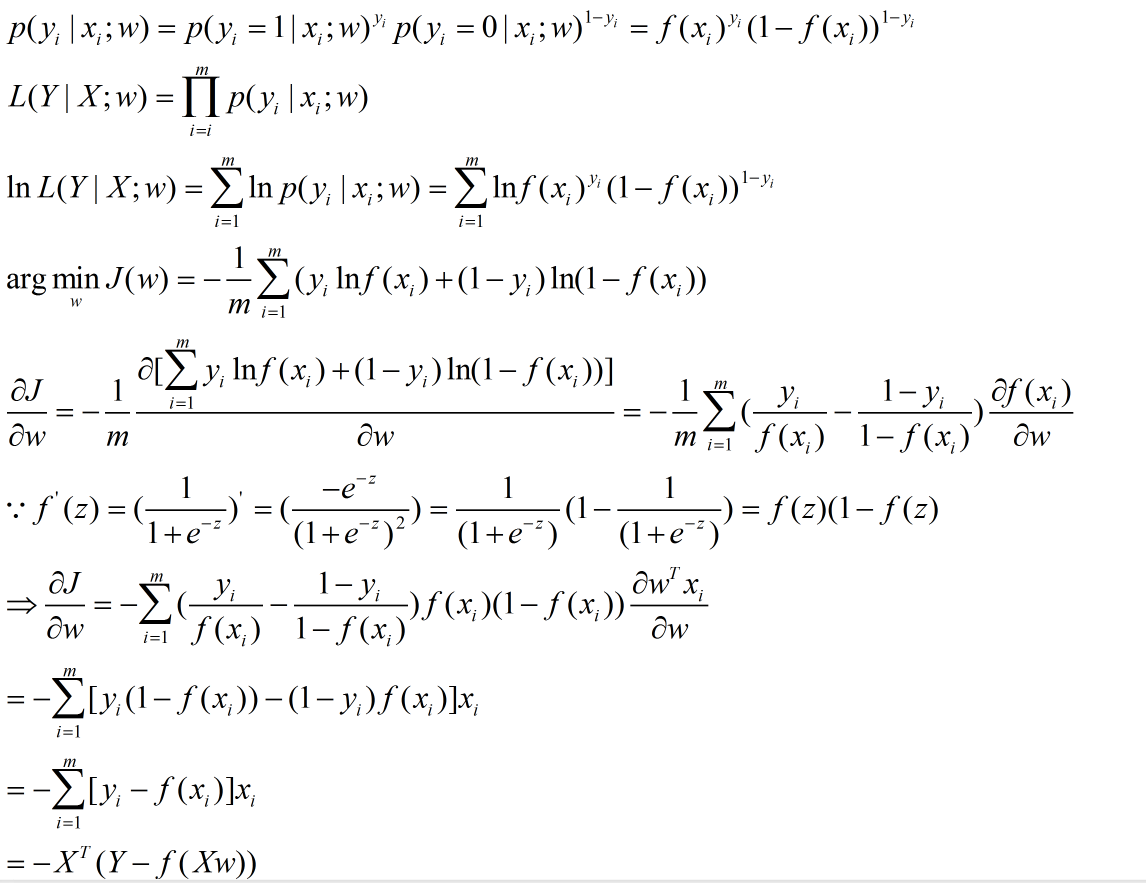
梯度下降法迭代公式

R語言實現

使用iris資料集

> head(iris)
  Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1          5.1         3.5          1.4         0.2  setosa
2          4.9         3.0          1.4         0.2  setosa
3          4.7         3.2          1.3         0.2  setosa
4          4.6         3.1          1.5         0.2  setosa
5          5.0         3.6          1.4         0.2  setosa
6          5.4         3.9          1.7         0.4  setosa
 

將資料分為訓練資料和測試資料

R語言使用批量梯度下降法迭代求解

iris2 = rbind(subset(iris, Species=='setosa'), subset(iris, Species=='versicolor'))
X <- cbind(rep(1, nrow(iris2)), iris2$Sepal.Length, iris2$Sepal.Width, iris2$Petal.Length, iris2$Petal.Width)
Y <- as.numeric(iris2$Species) - 1
maxIterNum <- 2000;
step <- 0.05;
W <- rep(0, ncol(X))
m = nrow(X)
sigmoid <- function(z) { 1 / (1 + exp(-z))}
for (i in 1:maxIterNum){
    grad <- t(X) %*% (sigmoid(X %*% W)-Y);
    if (sqrt(as.numeric(t(grad) %*% grad)) < 1e-8){
        print(sprintf('iter times=%d', i));
        break;
    }
    W <- W - grad * step;
}
print(W);
hfunc <- function(a) {if (a > 0.5) return(1) else return (0);}
myY = apply(sigmoid(X %*% W), 1, hfunc)
print(cbind(Y, myY))
 

輸出後，可以看到擬合完全正確，因為本文只是為了推導一下邏輯迴歸的演算法，所以直接用全部資料擬合，沒有再抽出一部分做測試資料。

總結

• 應該增加一部分訓練資料，驗證模型的正確性
• 應該增加正則項避免過擬合，比如L2正則