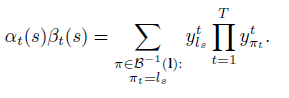論文筆記:Connectionist Temporal Classification: Labelling Unsegmented Sequence
標記未分割的序列資料是現實世界序列學習中普遍存在的問題,並且在一些感知任務中是普遍實用的,例如手寫字型識別,語音識別,手勢識別(gesture recognition)。在感知任務中,帶有噪聲的實值輸入流用一串離散的標籤進行標註。例如字母或者單詞。
當前,圖模型,例如HMM,CRFs和他們的變體是序列標註的主要框架,而這些方法已經被證明對很多問題有用,但他們也有一些缺點:
(1) 這些模型通常需要大量與任務相關的專業知識,例如設計HMMs的狀態模型,選擇CRFs的輸入特徵。
(2) 模型需要明顯的依賴假設使得推理可行(tractable,即多項式時間內可解)的,例如HMMs的觀察狀態的獨立性假設。
(3) 對於標準的HMMs,是生成式的訓練,但是序列標註是判別式的。
迴圈神經網路(RNNs),不需要任何先驗知識,出了輸入和輸出的表示之外,他們可以進行判別式訓練,他們的內部狀態提供了一個強有力且通用的機制為時間序列建模。另外,他們對於時間和空間的噪聲都是健壯的。
現在,對於序列標註,使用RNNs的方式是讓它結合HMMs構成的混合方法(hybrid approach),混合系統使用HMMs去為長序列結構(long-range sequential structure)的資料進行建模,神經網路提供區域性的分類。HMMs元件可以自動在訓練中切分序列,把網路分類轉換成標籤序列(labelsequences)。由於HMMs本身具有前述的侷限性,混合系統(hybrid systems)未能完全利用RNNs的序列建模的潛能。
貢獻
這篇文章提出了一個用RNNs標記序列資料的新方法,移除了預先分割訓練資料和後處理輸出的必要,模型只用了一個網路結構就能處理序列的所有問題。基本想法是在給定輸入序列的情況下,把網路的輸出作為所有可能標記序列的概率分佈。給定這個分佈,目標函式目標函式就可以直接得到最大概率的正確標記,目標函式是判別式的,所以這個網路可以用標準的反向傳播進行訓練。
Temporal Classification(時間分類)
S是一個服從一個固定分佈DX*Z的訓練樣例集合.輸入空間X=(Rm)*是一個集合所有序列的m維實數值向量.目標空間Z=L*是所有字母L的標記序列的集合。通常,我們把L*作為標記序列或者標籤,每一個S中的樣例由一對(x,z)序列組成.目標序列為z=(z1,z2,…,zU)最多和輸入序列x=(x1,x2,…,xT)一樣長,例如U<=T.因為輸入序列和目標序列通常不是一樣長的,所以沒有任何先驗的方式去對齊。
使用S去訓練一個時間分類器h:X->Z的目的是分類原先未見過的輸入序列,使得一些與任務相關的誤差評估最小。
Label Error Rate
給定一個測試集S’⸦DX*Z, S‘和S集合不相交,定義一個時間分類h的labelerror rate(LER)為平均歸一化編輯距離,編輯距離在S’上的分類和目標進行的。

ED(p,q)是序列p和q的編輯距離,即把p變為q所需要的插入,替換,刪除的最少次數。
最小編輯距離的實現就是一個遞迴,如果讀者不懂,可以自行百度了。Connectionist Temporal Classification
一個CTC網路有一個softmax輸出層,出了序列的輸出外,還增加了一個額外的輸出單元,最開始激勵的|L|個單元被解釋成在這個時刻對應標籤的觀察概率,激勵的額外的單元是一個空白的觀察概率或者無標籤的觀察概率。這些輸出定義為在給定輸入序列的情況下,所有可能的對齊所有標記序列的方式。標記序列的概率是所有可能對齊方式的概率和。
更正式的講,輸入序列x,長度為T,定義一個RNN,有m個輸入,n個輸出,權重向量w作為一個連續對映Nw:(Rm)->(Rn)T.讓y=Nw(x)為網路的序列輸出,ykt是單元k在時刻t的激勵。Ykt解釋為時刻t標記k的觀察概率,這定義了一個在集合L’T的長度為T的序列分佈,L’=L+{blank}:

L’T的所有元素,我們成為路徑,L‘T是所有路徑的集合,π表示其中的一個路徑。上式隱含的有一個假設,給定網路的內部狀態,網路在不同時刻的輸出是條件獨立的。這就要求輸出層沒有反饋連線到他自身或者網路。
下一步是定義多到一的對映β:L’T->L<=T,L<=T是可能標記的集合。我們簡單的移除所有的空白(blanks)和重複的標籤。
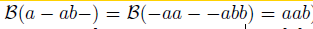
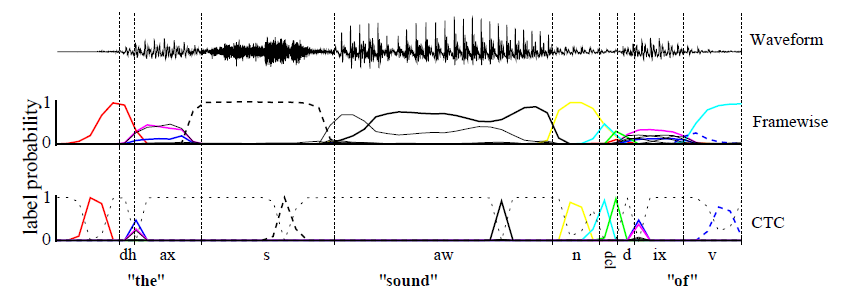
上圖是幀級(Framewise)和CTC網路分類一個語音訊號,陰影線是輸出激勵,對應特定時刻的音素的觀察概率,CTC僅僅預測音素序列(典型的一系列的尖狀物(a series of spikes),用blank分開了,或者沒有預測),幀級網路(framewise network)嘗試和人工分割的邊緣對齊(垂直的線)。幀級網路接收了一個錯誤的對齊邊界,雖然它預測了正確的音素(dh).當一個音素一直出現並靠近另一個音素時(dcl總是以d結尾),CTC預測的是一個雙尖狀物(a double spike)。標記的選擇可以直接從CTC的輸出進行得到,而幀級網路必須經過後處理(post-processed)才能獲得。
最終,β定義為一個給定序列l屬於L<=T的條件概率,條件概率是所有路徑的概率和。公式如下:

構造分類器
分類器的輸出應該是在給定輸入序列下的最可能的標記輸出,
利用HMMs,我們把尋找這個標記過程記為解碼,但是我們找不到一個通用並且tractable的解碼演算法,下面是兩個近似的演算法,在實踐中給出了良好的結果。
第一個方法是最佳路徑解碼(best path decoding),基於的假設:最可能的路徑會對應最可能表標籤,

最佳路徑解碼非常容易計算,π*僅僅就是每個時間步的最可能輸出的連線。但是它不能保證找到最有可能的標記。
第二種方法是字首查詢解碼(prefix search decoding),通過修改前向後向演算法(forward-backward algorithm),我們可以高效的計算出標記字首的後繼拓展的概率。

如圖,字首查詢解碼字母X,Y.每個節點要麼以“e”結尾,要麼從父節點進行拓展字首,在每個end節點上面的數字是單個標記重點在父節點的概率(The number above an end node is the probability of the single labelling ending at its parent,翻譯得雲裡霧裡,我就直接上原文了,看圖相信就會懂了),在每一次迭代中,對最可能留下字首的拓展進行探索。當有一個標記(這裡是’XY’)比其他標記的概率更大時,搜尋就終止了。
一個訓練的CTC網路的輸出傾向於形成一系列的尖狀物(spikes),尖狀物被預測的blanks分隔開,我們把輸出的序列分為幾部分,這幾個部分可能都是是以一個blank開始和結尾。我們選擇邊界點,這些邊界點的是blank標記的觀察概率超過一個給定的閾值,然後我們對每個部分計算器最可能的標記序列,然後把他們連線起來得到最終的分類。
實踐中,字首搜尋在這個啟發式下工作得很好,通常超過了最佳路徑解碼,但是在有些情況下,效果不佳,例如,當相同的標籤在一個部分邊界的兩側都概率很低(if the same label is
predicted weakly on both sides of a section boundary,這個我也不是很明白,直接上原文)。
網路訓練
目標函式是從最大似然估計的規則中衍生出來的,即最小化log似然估計目標序列。給定目標函式,它的導數和網路輸出有關,因此我們可以通過標準的反向傳播計算權重梯度,網路通過任何基於梯度優化演算法進行訓練,
前向後向演算法
我們需要一個高效的方式去計算每一個標記的條件概率p(l|x),乍一看,對一個給定標籤的所有路徑求和似乎有些不可能,通常,路徑太多了。
這個問題可以用動態規劃演算法(dynamic programming algorithm)解決,類似於HMMs的前向後向演算法,核心思想是對一個標記的所有路徑求和可以被分解為一個迭代路徑的求和,路徑對應標記的字首,這個迭代過程可以用遞迴的前向和後向變數高效的計算。
對於一些長度為r的序列q,用q1:p表示開始的p個符號,qr-p:r表示最後的p個符號。然後對於一個標記l,定義前向變數αt(s),表示在時刻t,l1:s的概率和。

Αt(s)可以遞迴的用αt-1(s)和αt-1(s-1)進行遞迴計算。
考慮到輸出路徑中海油空白(blanks),我們在每一對標籤之間插入了空白,在開始和末尾也加入了空白,這樣我們用l‘表示這個新的標記,l’的長度就為2|l|+1’.在計算l’字首的概率中,我們允許空白和非空白標籤之間轉移,我們允許所有的字首要麼以一個空白(b)開始,要麼是l(l1)的第一個標籤開始.
公式如下:


加這個條件是因為這些變數對應的狀態沒有留下足夠的時間步去完成這個序列,如下圖右上角未連線的圓圈:

前向後向演算法運用到標記‘CAT’序列的例子,黑圈代表標籤(labels),白圈代表空白。箭頭代表允許的轉移。前向變數王箭頭方向進行跟新,後向變數往箭頭的反方向更新。
L的概率是l’所有概率的求和,並且去除了T時刻的最後的blank得到的。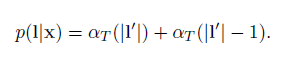
同樣,後向變數βt(s)是t時刻ls:|s|的概率和,

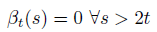


實際上,上面的遞迴將會迅速導致任何電腦的下溢,因此,我們需要變換一下。用α^代替α,用β^代替β


為了評估最大似然誤差,我們需要用到自然對數。
極大似然訓練(一大波公式來襲,不過按照它的推導 也很容易)
訓練的目標是同時最大化訓練集上所有正確分類的log概率,意味著優化下式:

為了用梯度下降訓練網路,我們需要就網路輸出進行微分(differentiate),訓練樣例是獨立地,我們可以單獨來考慮
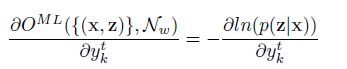
我們可以用前向後向演算法計算上式。主要思想是:對於一個標記l,在給定s和t的情況下,前向和後向變數的內積是對應l所有可能路徑的概率。表示式為: