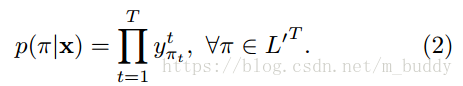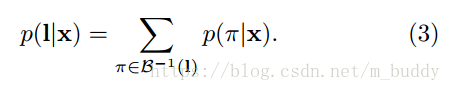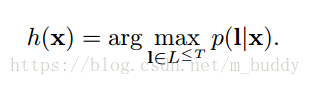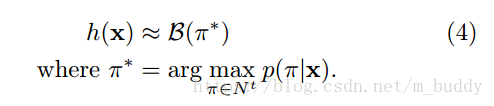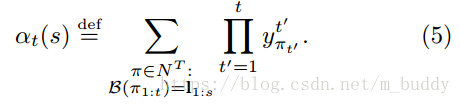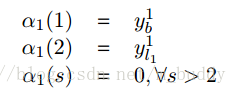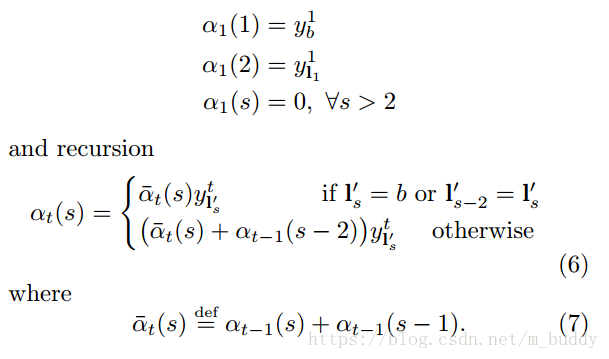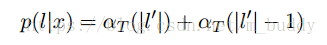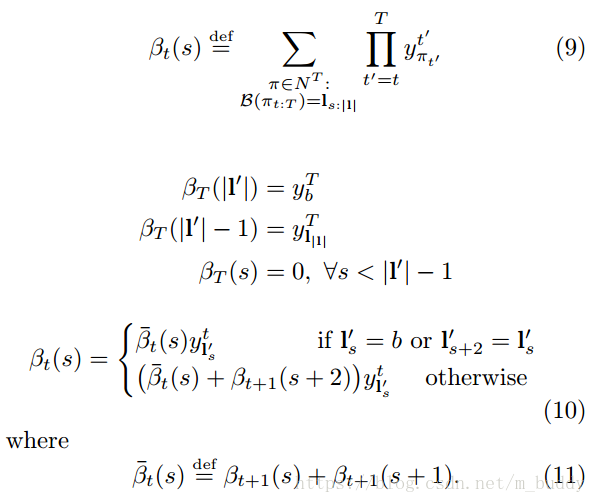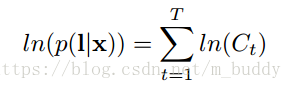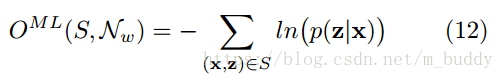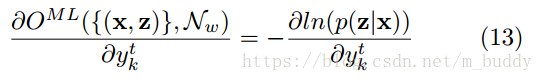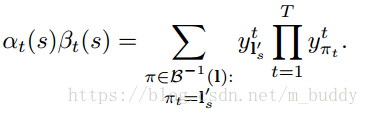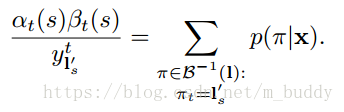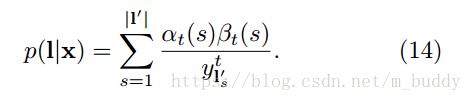1. 思想

序列學習任務需要從未分割的輸入資料中預測序列的結果。HMM模型與CRF模型是序列標籤任務中主要使用的框架，這些方法對於許多問題已經獲得了較好的效果，但是它們也有缺點：
（1）需要大量任務相關的知識，例如，HMM中的狀態模型，CRF中的輸入特徵選擇；
（2）需要有獨立性假設作為支撐；
（3）對於標準的HMM模型，它是生成式的，但是序列標籤時判別式的。

RNN網路除了出入與輸出的表達方式需要選擇之外不需要任何資料的先驗。它可以進行判別訓練，它的內部狀態為構建時間序列提供了強大的通用機制。此外，其對時間和空間噪聲具有很強的魯棒性。

但是對於RNN呢，它是不能拿來做序列預測的，這是因為RNN只能去預測一些獨立標籤的分類，因而就需要進行序列預分割。要解決該問題，那麼將RNN與HMM結合起來被稱之為hybrid approach。在該方法中使用HMM為長序列結構資料建立模型，神經網路就提供區域性分類。加入HMM之後可以使得在訓練中自動分割序列，並且將原本的網路分類轉換到標籤序列。然而，它並沒有避免上訴內容中HMM使用缺點。

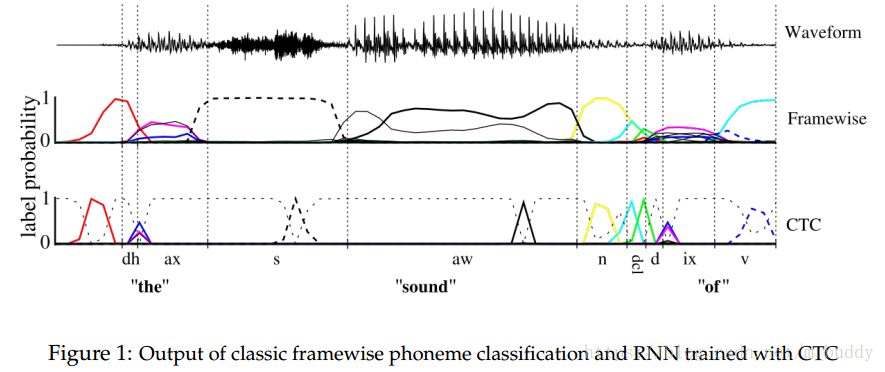
這篇文章提出了CTC( Connectionist Temporal Classification)，可以解決前面提到的兩點侷限，直接使用序列進行訓練。CTC引入了一個新的損失函式，可以使得RNN網路可以直接使用未切分的序列記性訓練。為了使用這個損失函式，為RNN引入其可以輸出的“blank”標籤。RNN的輸出是所有標籤的概率。

RNN可以輸出“blank”的好處：
（1）RNN可以選擇任意時刻給出一個標籤，例如在沒有資訊輸入的音訊空白時間給“blank”標籤，其它則出處對應的標籤；
（2）“blank”標籤可以在某一時刻對一個正確的標籤給一個很高的概率，在之前我們是檢視此時所有標籤的概率分佈。

2. Temporal Classification

這裡將Temporal Classification定義為 $h$，訓練資料集合 $S$中資料是成對存在的 $($

x , z ) (x, z) ，其中 $x$是訓練的時序資料， $z$是標籤資料。目標就是找到一個時序分類器 $h$使得 $S$中的 $x$被分類到 $z$。訓練這個分類器，就需要一個錯誤度量，這裡就借鑑了ED距離度量，而引入了label error rate（LER）。在這裡還對其進行了歸一化，從而得到了如下的形式：
$LER(h,S^{,})=\frac{1}{Z} \sum_{(x,z) \in S^{'}}ED(h(x))------(1)$

3. 時序分類器

這一部分是最為關鍵的一步，將網路輸出轉換成為基於標籤序列的條件概率，從而可以使用分類器對輸入按照概率大小進行分類。

3.1 從網路輸出到連續標籤

在CTC網路中擁有一個softmax輸出層，其輸出的個數為 $|L|+1$， $L$是標籤元素的集合，額外的一個那當然就是“blank”標籤了。這些輸出定義了將所有可能的標籤序列與輸入序列對齊的所有可能路徑的概率。任何一個標籤序列的總概率可以通過對其不同排列的概率求和得到。

首先，對於一條可行的路徑 $p(\pi |x)$被定義為，對應路徑上各個時刻輸出預測概率的乘積。其定義如下：

對於預測結果中的一條路徑的標籤，在論文中假設的是這些不同時刻網路的輸出是相互獨立的，而這是通過輸出層與自身或網路之間不存在反饋連線來確保實現的。

在此基礎上還定義了對映函式 $B$，它的職責就是去除“blank”與重複的標籤。因而給定的一個標籤其輸出概率就可以描述為幾個可行路徑相加和的形式：

3.2 構建分類器

在上面的內容中已經得到了一個序列標籤的輸出條件概率，那麼怎麼才能找到輸入資料最匹配的標籤呢？最為直觀的便是求解 $argmax$了

在給定輸入情況下找到其最可能的標籤序列，這樣的過程使用HMM中的術語叫做解碼。目前，還沒有一種通過易理解的解碼演算法，但下面的兩種方法在實踐過程中也取得了不錯的效果。

3.2.1 最佳路徑解碼

該方法是建立在概率最大的路徑與最可能的標籤時對應的，因而分類器就被描述為如下形式：

從上面的形式中就可以看出，最佳路徑解碼的計算式很容易的，因為最佳路徑中的元素是各個時刻輸出的級聯。但是呢，這是不能保證找到最可能的標籤的。

3.2.2 字首解碼

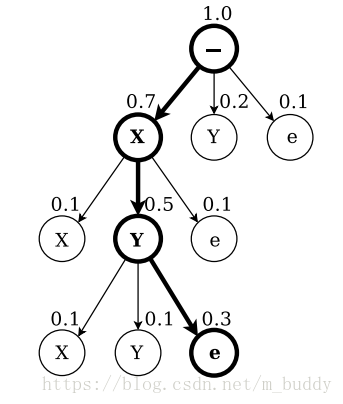
通過修改論文中4.2節的前向和後向演算法，便可以有效計算標籤字首的連續擴充套件概率，見下圖

字首解碼在足夠時間的情況下會找到最可能的標籤，但是隨著輸入序列長度的增強時間也會指數增加。如果輸入的概率分佈是尖狀的，那麼可以在合理的時間內找到最可能的路徑。

實踐中，字首搜尋在這個啟發式下工作得很好，通常超過了最佳路徑解碼，但是在有些情況下，效果不佳。

4. 網路訓練

目標函式是由極大似然原理匯出的。也就是說，最小化它可以最大化目標標籤的對數可能性。有了損失函式之後就可以使用依靠梯度進行優化的演算法進行最優化。

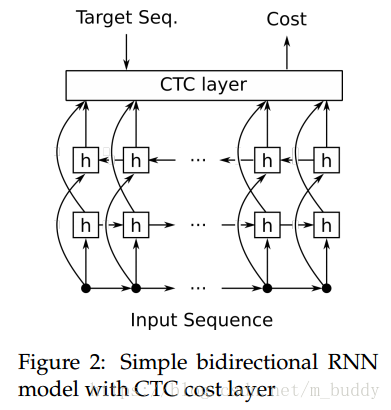
4.1 CTC的網路結構

在下圖中給出了CTC放置的位置，其放置在雙向遞迴網路的後面作為序列預測的損失來源。CTC會在RNN網路中傳播梯度，進而使得其學習一條好路徑。

4.2 CTC前向傳播演算法與反向傳播演算法

4.2.1 前向傳播

需要一種有效的方法來計算單個標籤的條件概率 $p(l|x)$。對於這樣問題，其實是對應於給定標籤的所有路徑的總和，通常有很多這樣的路徑。這裡採用使用動態規劃演算法計算所有可能路徑的概率和，其思想是，與標籤對應的路徑和可以分解為與標籤字首對應的路徑的迭代和。
然後，可以使用遞歸向前和向後變數有效地計算迭代。

以下是本文設計到的一些符號定義：
$y_{k}^{t}$，時刻 $t$的輸出字元 $k$
$l$，標籤序列對應的損失
$l^{'}$，相同的標籤序列，但是在字元之間添加了“blank”標籤

其中， $B$是移除所有“blank”與重複字元的變換； $\pi \in N^T:B(\pi _{1:t}=l_{1:s}^{'}$是時刻1到t的預測矩陣中，給出經過變換 $B$之後與標籤有前s個一致的所有可行路徑； $y^{t^{'}}$是指時刻 $t^{'}$時RNN的輸出。而且 $\alpha_{t}(s)$可以通過 $\alpha_{t-1}(s)$與 $\alpha_{t-1}(s-1)$迭代計算出來。

圖3中描述的狀態轉移圖與上面公式的含義是相同的。為了能夠在輸出路徑中出現“blank”標籤，將標籤修改成了 $l^{'}$，也就是在標籤的前後與字元之前插入空白標籤，因而生成的標籤長度就變成了 $2|l|+1$的長度，使其可以再空白標籤與非空白標籤之間轉換，也可以使非空白標籤之間發生轉換。

上面的公式1中已經給出了其計算的內容，但其計算並不具有可行性。但是可以根據圖3中 $\alpha_{t}(s)$的遞迴定義使用動態規劃演算法去解決該問題，仔細看這幅圖，是不是有點像HMM的前向計算過程。

對於解決該問題使用動態規劃的演算法進行解決，首先來分析時刻1時候的情況：

對於後序狀態的關係推導

最後就可以得到一個序列的輸出概率

4.2.1 反向傳播

反向傳播的變數 $\beta_{t}(s)$被定義為 $t$時刻 $l_{s:|l|}$的總概率

注意： $\beta_{t}(2)=0 \forall s \gt 2t and s \gt |l^{’}|$，可見與圖3的左下角處未連線的圓圈。在實踐中上述的計算過程通常會導致數值下溢，其中的一種解決辦法就是對其進行歸一化操作，對於前向傳播演算法這裡定義瞭如下作

對於反向傳播演算法中，也是有類似的定義的

最後的最大似然誤差，也是建立在此基礎之上的

4.3 最大似然訓練

最大似然訓練的目的是同時最大化訓練集中所有正確分類的對數概率。因而這裡可以將損失函式定義為：

為了使用梯度進行網路訓練，因而就需要對網路的輸出進行微分，且訓練樣本是相互獨立的，也就是說可以單獨考慮了，因而可以將微分寫為：

這裡可以用前向後向演算法計算上式。主要思想是：對於一個標記l，在給定s和t的情況下，前向和後向變數的內積是對應l所有可能路徑的概率。表示式為：

且根據上面的公式（2）聯合可以得到：

再與前面的公式（3）聯合可以得到

由於網路的輸出是條件獨立的，我們需要考慮路徑在時刻t經過標記k，得到 $p(l|t)$的偏導數，這是對於 $y_k^t$而言的，注意到相同的標籤肯能會重複幾次再一個標記l中，我們定義了一個位置集合，標籤k出現，記為 $lab(l,k)={s:l_s^{'}=k}$

相關推薦