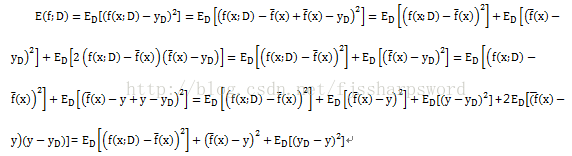2.模型評估與選擇

2.1經驗誤差和過擬合

不同學習演算法及其不同引數產生的不同模型，涉及到模型選擇的問題，關係到兩個指標性，就是經驗誤差和過擬合。

1）經驗誤差

錯誤率(errorrate)：分類錯誤的樣本數佔樣本總數的比例。如果在m個樣本中有a個樣本分類錯誤，則錯誤率E=a/m，相應的，1-a/m稱為精度（accuracy），即精度=1-錯誤率。

誤差(error)：學習器的實際預測輸出和樣本的真實輸出之間的差異。訓練誤差或經驗誤差：學習器在訓練集上的誤差；泛化誤差：學習器在新樣本上的誤差。

自然，理想情況下，泛化誤差越小的學習器越好，但現實中，新樣本是怎樣的並不知情，能做的就是針對訓練集的經驗誤差最小化。

那麼，在訓練集上誤差最小、甚至精度可到100%的分類器，是否在新樣本預測是最優的嗎？

我們可以針對已知訓練集設計一個完美的分類器，但新樣本卻是未知，因此同樣的學習器（模型）在訓練集上表現很好，但卻未必在新樣本上同樣優秀。

2）過擬合

學習器首先是在訓練樣本中學出適用於所有潛在樣本的普遍規律，用於正確預測新樣本的類別。這會出現兩種情況，導致訓練集上表現很好的學習器未必在新樣本上表現很好。

過擬合(overfitting)：學習器將訓練樣本的個體特點上升到所有樣本的一般特點，導致泛化效能下降。

欠擬合(underfitting)：學習器未能從訓練樣本中學習到所有樣本的一般特點。

通俗地說，過擬合就是把訓練樣本中的個體一般化，而欠擬合則是沒學習到一般特點。一個是過猶不及；一個是差之毫釐。過擬合是學習能力太強，欠擬合是學習能力太弱。

欠擬合通過調整模型引數可以克服，但過擬合確實無法徹底避免。機器學習的問題是NP難，有效的學習演算法可在多項式時間內完成，如能徹底避免過擬合，則通過經驗誤差最小化就能獲得最優解，這樣構造性證明P=NP，但實際P≠NP，過擬合不可避免。

總結，在模型選擇中，理想的是對候選模型的泛化誤差進行評估，選擇泛化誤差最小的模型，但實際上無法直接獲得泛化誤差，需要通過訓練誤差來評估，但訓練誤差存在過擬合現象也不適合作為評估標準，如此，如何進行模型評估和選擇呢？

2.2評估方法

評估模型既然不能選擇泛化誤差，也不能選擇訓練誤差，可以選擇測試誤差。所謂測試誤差，就是建立測試樣本集，用來測試學習器對新樣本的預測能力，作為泛化誤差的近似。

測試集，也是從真實樣本分佈中獨立同分布取樣而得，和訓練集互斥。通過測試集的測試誤差來評估模型，作為泛化誤差的近似，是一個合理的方法。對資料集D={（x₁,y₁）, （x₂,y₂）,…, （x_m,y_m）}進行分隔，產生訓練集S和測試集T，通過訓練集生成模型，並應用測試集評估模型。文中有個很好的例子，就是訓練集相當於測試題、而測試集相當於考試題。

現在我們將問題集中在測試集的測試誤差上，用以評估模型。那重要的是，對資料集D如何劃分成訓練集和測試集從而獲得測試誤差？

1）留出法

留出法(hold-out)將資料集D劃分為兩個互斥的集合，其中一個集合用作訓練集S，另一個作為測試集T，即D=SUT，S∩T=∅。在S上訓練出的模型，用T來評估其測試誤差，作為對泛化誤差的近似估計。

以二分類任務為例。假定D包含1000個樣本，將其劃分為700個樣本的訓練集S和300個樣本的測試集T。用S訓練後，模型在T上有90個樣本分類錯誤，那麼測試誤差就是90/300=30%，相應地，精度為1-30%=70%。

留出法就是把資料集一分為不同比例的二，這裡面就有兩個關鍵點，一個就是如何分？另一個就是分的比例是多少？

如何分呢？訓練集和測試集的劃分要保持資料分佈的一致性。何意？分層取樣，保持樣本的類別比例相似，就是說樣本中的各類別在S和T上的分佈要接近，比如A類別的樣本的比例是S:T=7:3，那麼B類別也應該接近7:3這個分佈。

在分層取樣之上，也存在不同的劃分策略，導致不同的訓練集和測試集。顯然，單次使用留出法所得到的估計結果不夠穩定可靠，一般情況下采用若干次隨機劃分、重複進行試驗評估後取平均值作為評估結果。

S和T各自分多少呢？若訓練集S過多而測試集T過小，S越大越接近D，則訓練出的模型更接近於D訓練出的模型，但T小，評估結果可能不夠穩定準確；若訓練集S偏小而測試集T偏多，S和D差距過大，S訓練的模型將用於評估，該模型和D訓練出的模型可能有較大差別，從而降低評估結果的保證性（fidelity）。S和T各自分多少，沒有完美解決方法，通常做法是二八開。

2）交叉驗證法

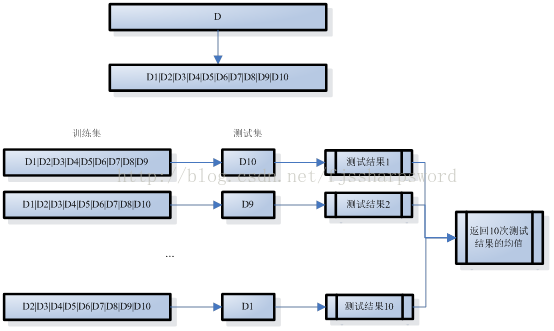
交叉驗證法(crossvalidation)將資料集D劃分為k個大小相似的互斥子集，即D=D₁UD₂U…UD_k，D_i∩D_j=∅（i≠j）；每個子集D_i都儘可能保持資料分佈的一致性，即從D中通過分層取樣所得。訓練時，每次用k-1個子集的並集作為訓練集，餘下的一個子集作為測試集；如此，可獲得k組訓練集和測試集，從而進行k次訓練和測試，最終返回k次測試結果的均值。k值決定了交叉驗證法評估結果的穩定性和保真性，因此也稱為k折交叉驗證或k倍交叉驗證，k常取值10、5、20，10折交叉驗證示意圖如下：

和留出法一樣，將資料集D劃分為k個子集也是多樣劃分方式，為減小樣本劃分不同而發生的差別，k折交叉驗證通常隨機使用不同的劃分重複p次，最後評估結果是這p次k折交叉驗證結果的均值，如10次10折交叉驗證。

典型的劃分特例留一法(Leave-One-Out，LOO)，假設資料集D中包含m個樣本，令k=m，就是每個子集只包含一個樣本。這個特例，不受隨機樣本劃分方式的影響，且訓練集S只比資料集D少一個樣本，其實際訓練出的模型和期望評估的用D訓練出的模型相似，其評估結果比較準備。當然，問題就是一個樣本一個子集，一旦樣本過大，訓練的模型所需開銷也是極其龐大，且其評估結果也未必比其他方法準確。

實際，所有演算法都是如此，有其優點有其缺點，各有適用場合，符合價效比原則。比如留一法，為了提升理論上的準確性，而犧牲相對明確龐大的開銷，效益上是否可取，那要看場合了。

3）自助法

在留出法和交叉驗證法中，訓練集S的樣本數是小於資料集D，因樣本規模不同會導致所訓練的模型及評估結果偏差。留一法雖然S只少一個樣本，但計算規模龐大。那麼有沒辦法避免樣本規模影響且能高效計算呢？

自助法，基於自助取樣獲取訓練集和測試集。給定包含m個樣本的資料集 ,如何通過自助取樣（可重複取樣或有放回取樣）產生資料集D’呢？自助取樣基本過程是：每次隨機從D中選一個樣本，放入D’，然後將該樣本放回初始資料集D中，使得該樣本在下次取樣時仍有可能被採到；這個過程重複執行m次後，就得到了包含m個樣本的資料集D’，規模和D一樣，不同的是，D’中部分樣本可能重複也有部分樣本可能不出現。一個樣本在m次自助取樣中都沒有被採到的概率是(1-1/m)^m，取極限得到：

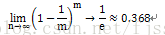
即通過自助取樣，初始資料集D中約有36.8%的樣本未出現在取樣資料集D’中。自助取樣後 ，將樣本規模和資料集D一樣的取樣資料集D’作為訓練集S=D’，將T=D-D’作為測試集（不在D’中的樣本作為測試集）。如此，實際評估的模型（訓練集S訓練出的）與期望評估的模型（資料集 D訓練出的）使用了同樣的樣本規模（m個樣本），同時又有大概36.8%的樣本（未在取樣資料集D’中）作為測試集T用於測試，產生的測試結果，稱為包外估計（out-of-bag estimate）。

每個演算法都有自己的使用場合，並不是萬能性地好用高效。自助法自助取樣產生的資料集D’也是改變了初始資料集D的分佈，也會引入估計偏差。自助法適用於資料集較小、難以有效劃分訓練集和測試。在初始資料量足夠時，留出法和交叉驗證法更常用一些。

為更好地對模型（學習器）進行泛化效能評估，提出了近似的測試誤差來評估泛化誤差，也就衍生出了留出法、交叉驗證法、自助法的資料集劃分方法。實際上，演算法還需要調參，不同的引數配置，模型的效能會有一定差別。在進行模型評估和選擇時，除了選擇演算法還有資料集劃分方法外，還需要對演算法引數進行設定或說是調節。每一個演算法都有引數設定空間，假定演算法有3個引數，每個引數有5個可選值，對每一組訓練集/測試集來說就有5³=125個模型需要考察。

實際的學習過程中，對給定包含m個樣本的資料集D，先選定學習演算法及其引數，然後劃分資料集訓練和測試，直至選定演算法和引數，再應用資料集D來重新訓練模型。在研究對比不同演算法的泛化效能時，用測試集上的判別效果來評估模型在實際使用中的泛化能力，而把訓練資料另外劃分為訓練集和驗證集，基於驗證集上的效能進行模型選擇和調參。

梳理下幾個要點：1）將資料集劃分為：訓練集、驗證集、測試集；2）訓練集用於訓練出模型，驗證集用於模型選擇和調參，測試集用於近似評估泛化誤差；3）模型評估方法有留出法、交叉驗證法、自助法，用於演算法選擇及引數設定。

2.3效能度量

通過在訓練過程中的評估方法來判定學習器的泛化效能，還需要通過效能度量來考察。換句話來說，選什麼模型，通過訓練集、驗證集、測試集來實驗評估選定並輸出；而所輸出的模型，在測試集中實的泛化能力，需要通過效能度量工具來度量。這樣理解，基於測試誤差近似泛化誤差的認定，通過劃分資料集為訓練集、驗證集、測試集，並選擇不同的評估方法和調整演算法引數來輸出的模型，需要通過效能度量的工具來量化評估。

不同的效能度量，在對比不同模型能力時，會導致不同評判結果，因為模型的好壞是相對的。實際模型的好壞，取決於演算法和資料，取決於訓練中調參和實驗評估方法，也取決於當前任務的實際資料。

模型訓練出來後，進行預測時，給定樣例集D={（x₁,y₁）, （x₂,y₂）,…, （x_m,y_m）}，其中y_i是示例x_i的真實標記，要評估學習器f的效能，把學習器預測結果f(x)與真實標記y進行比較。

預測迴歸任務最常用的效能度量是均方誤差(mean squared error)：

真實情況	預測結果
	正例	反例
正例	TP（真正例）	FN（假反例）
反例	FP（假正例）	TN（真反例）

查準率P和查全率R分別定義為：

P=TP/(TP+FP)

R=TP/(TP+FN)

查準率和查全率是一對矛盾的度量，一般來說，查準率高時，查全率往往偏低；而查全率高時，查準率往往偏低。在資訊檢索中，查準率就是檢索出的資訊有多少比例是使用者感興趣的；查全率則是使用者感興趣的資訊有多少被檢索出來。查準率分母中就包含了那些不是使用者感興趣的資訊，但仍被預測為是使用者感興趣的而被檢索出來；查全率分母中則包含了那些是使用者感興趣的資訊，但為被預測為使用者感興趣而被拋棄未檢索出來。

可根據學習器的預測結果對樣例進行排序，排在前面的是學習器認為最可能是正例的樣本，排在最後的則是學習器認為最不可能是正例的樣本。按此順序逐個把樣本作為正例進行預測，則每次可以計算出當前的查全率、查準率，並以查準率為縱軸、查全率為橫軸構造查準率-查全率曲線，簡稱P-R曲線。

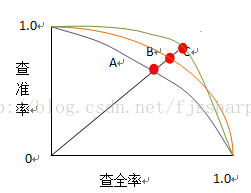
P-R曲線是非單調、不平滑的。P-R曲線可用來評估學習器的優劣。若一個學習器的P-R曲線被另一個學習器的P-R曲線完全包住，則後者的效能優於前者。如果兩個學習器的曲線發生交叉，則通過二者面積的大小來比較，面積大的表示查全率和查準率雙高比較優秀，但不太容易計算曲線（不平滑）的面積，因此通過平衡點（Break-Even Point，簡稱BEP）來度量。BEP是座標上查準率等於查全率時的點，平衡點值越大，學習器越優秀。

用了簡單的圖來說明，紅色的點就是三條P-R曲線的BEP點，學習器A的曲線被C包住，C比較優秀，而C和B交叉，用面積計算難以估算，但C的BEP值大於B，所以C比較優秀。

ERP過於簡化，定義F1常量來比較學習器P-R曲線的效能：

F1=2*P*R/P+R=2*TP/(樣例總數+TP-TN)

不同的應用場合，對查全率和查準率的側重不同，如在商品推薦中，為儘可能少打擾使用者，希望推薦的內容卻是使用者所感興趣的，查準率更重要；在逃犯資訊檢索中，希望儘可能少漏掉逃犯，此時查全率更重要。對查準率和查全率的不同偏好，可用F1度量的一般形式F_β，定義為：

F_β=(1+β²)*P*R/((β²*P)+R)

其中β>0度量了查全率對查準率的相對重要性；β=1時就是標準的F1；β>1時偏好查全率；β<1時偏好查準率。

F1是基於查準率和查全率的調和平均（harmonic mean）定義：

1/F1=1/2*(1/P+1/R)

F_β則是加權調和平均：

1/ F_β=1/(1+β²)*(1/P+β²/R)

與算術平均（P+R）/2和幾何平均 相比，調和平均更重視較小值。

幾何平均數：N個數據的連乘積的開N次方根。

算術平均數：一組資料的代數和除以資料的項數所得的平均數.

調和平均數：一組資料的倒數和除資料的項數的倒數。

平方平均數：一組資料的平方和除以資料的項數的開方。

對同一資料，調和≤幾何≤算術≤平方。

進行多次訓練和測試、在多個數據集上進行訓練和測試、執行多分類任務時每兩兩類別組合對應的混淆矩陣，這些情況系下產生的多個混淆矩陣，需要估計演算法的全域性效能，即在n個二分類混淆矩陣上考察查準率和查全率，從而評估模型效能。這個有兩種做法，一個是求得P和R再平均；另一個是直接對TP、FP、TN、FN求取平均值後再得P和R值；分別為巨集查全率和巨集查準率、微查全率和微查準率。

3）ROC與AUC

很多學習期為測試樣本產生一個實值或概率預測，然後將這個預測值和分類閾值進行比較，若大於閾值則分類正類，否則為反類。對測試樣本的實值或概率預測結果進行排序，最可能是正例的排在最前面，最不可能是正例的排在最後面。分類過程就相當於在這個排序中以某個截斷點將樣本分為兩部分，前一部分判為正例，後一部分則判為反例。

在不同的應用任務中，可根據任務需求來採用不同的截斷點，選擇排序中靠前的位置進行截斷重視查準率；選擇靠後的位置進行截斷則重視查全率。排序本身的質量好壞，體現了學習器在不同任務下的期望泛化效能的好壞，或者說，一般情況下泛化效能的好壞。ROC曲線正是考量期望泛化效能的效能度量工具，適用於產生實值或概率預測結果的學習器評估。

ROC（ReceiverOperating Characteristic，受試者工作特徵），根據學習器的預測結果對樣例進行排序，按此順序逐個把樣本作為正例進行預測，每次計算出兩個重要量的值，分別作為橫、縱座標，即得到ROC曲線。

ROC曲線的縱軸是真正例率（The Positive Rate,TPR），橫軸是假正例率（FalsePositive Rate,FPR），分別定義為：

真正例率：TPR=TP/(TP+FN)，預測的真正例數和實際的正例數比值，有多少真正的正例預測準確；

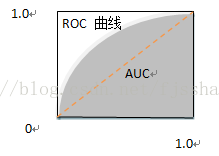
假正例率：FPR=FP/(TN+FP)，預測的假正例數和實際的反例數比值，有多少反例被預測為正例；

從圖中可以看出ROC曲線的對角線對應於隨機猜測模型，而點（0，1）則對應於將正例排在所有反例之前的理想模型，真正例率是100%。

在實際任務中，樣本是有限的，所以不能產生光滑的ROC曲線，而是帶有齒狀的近似ROC曲線。有限個測試樣例ROC圖繪製方法：給定m⁺個正例和m^-個反例，根據學習器預測結果對樣例進行排序，開始把分類閾值設為最大（所有樣例均預測為反例），此時真正例率和假正例率均為0，在座標（0,0）處標記一個點；然後，依次將分類閾值設為每個樣例的預測值（依次將每個樣例劃分為正例），並求解真正例率和假正例率，在相應的座標處標記一個點。設前一個標記點座標為（x,y），當前若為真正例，則對應比較點的座標為（x,y+1/ m⁺）；當前若為假正例，則對應標記的點的座標為（x+1/ m^-，y），最後用線段把相鄰的點連線起來即得近似ROC曲線。

接著，自然是要說到用ROC曲線怎麼比較學習器的優劣呢？和P-R曲線相似，若一個學習器的ROC曲線被另一個學習器的曲線完成包住，則後者的效能優於前者。若兩個學習器的ROC曲線發生交叉，要進行比較的話，就需要比較ROC曲線下的面積，即AUC（AreaUnder ROC Curve）。

AUC可通過對ROC曲線下各部分的面積求和而得。假定ROC曲線是由座標為{（x₁,y₁）, （x₂,y₂）,…, （x_m,y_m）}的點按序連結而形成（x₁=0，x_m=1），則AUC估算為：

真實類別	預測類別
	第0類	第1類
第0類	0	cost01
第1類	Cost10	0

如上表，整體學習器效能評估上，不是考慮最小化錯誤次數，而是最小化總體代價。假設上表的第0類為正類，第1類為反類，令D⁺和D^-分別表示正、反例集合，則代價敏感（cost-sensitive）錯誤率為：

其中FPR是假正例率，FNR=1-TPR是假反例率。代價曲線的繪製：ROC曲線上的每一點對應了代價平面上的一條線段，設ROC曲線上點的座標為（TPR,FPR），則可相應計算出FNR，然後在代價平面上繪製一條從（0,FPR）到（1,FNR）的線段，線段下的面積表示了該條件下的期望總體代價。如此，將ROC曲線上的每個點轉化為代價平面上的一條線段，然後去所有線段的下界，圍城的面積即為在所有條件下學習器的期望總體代價。

5）總結

對學習器的效能度量是選擇學習器的參考，下面對幾個效能度量指標進行分類：

類別	效能度量指標
	均等代價	非均等代價
預測分類的學習器	P-R曲線和F1	代價敏感錯誤率
預測實值的學習器	ROC曲線和AUC	代價曲線

對於常用的錯誤率和精度，也是用於預測分類的學習器效能度量。實際上，不同的任務需要採用不同的指標來度量，同時在指標上具體的側重也不同。

2.4比較檢驗

對學習器的效能評估，基於測試集已經給出了評估方法和衡量模型泛化能力的效能度量工具，那麼是否就可以通過對效能度量的值比較來評估學習器優劣呢？顯然答案不是那麼肯定，因為測試集上的效能評估方法和度量工具始終還是測試集上的，與測試集本身的選擇有關係，且機器學習演算法本身存在一定隨機性。統計假設檢驗（hypothesis test）為學習器效能比較提供了重要依據。

基於假設檢驗結果可推斷出，在測試集上觀察到的學習器A優於B，則A的泛化效能是否在統計意義上好於B，以及這個判定的準確度。也就是說，在測試集上的評估和度量，放在統計意義上進一步檢驗。以錯誤率為效能度量工具，用e表示，介紹假設檢驗方法。

1）單個學習器的假設檢驗

假設檢驗中的假設是對學習器泛化錯誤率分佈的某種判斷或猜想。在統計意義上，對泛化錯誤率的分佈進行假設檢驗。現實任務中，只知測試錯誤率，而不知泛化錯誤率，二者有差異，但從直觀上，二者接近的可能性較大，而相差很遠的可能性很小，因此可基於測試錯誤率推出泛化錯誤率的分佈。

實際上，評估方法和效能度量，正式基於上面這一統計分佈直觀思維來開展，這裡更是通過假設檢驗來進一步肯定測試錯誤率和泛化錯誤率二者接近。

資料集	演算法A	演算法B	演算法C
D1	1	2	3
D2	1	2.5	2.5
D3	1	2	3
D4	1	2	3
平均序值	1	2.125	2.875

2.5偏差與方差

通過實驗方法估計的泛化效能，還需要解釋其具有這樣效能的原因，回答為什麼具有這樣的效能。偏差-方差分解是解釋學習演算法泛化效能的一種重要工具。

梳理下模型評估與選擇的整個思路：首先模型評估面臨經驗誤差和過擬合現象，因此引入測試集，通過測試誤差率近似泛化誤差率來評估模型，提出了評估方法，並量化度量效能，在此基礎上通過假設檢驗為效能度量提供依據，最後解釋效能，即偏差-方差分解。

偏差-方差分解對學習演算法的期望泛化錯誤率進行拆解。演算法在不同訓練集上學得的結果很可能不同，即便這些訓練集是來自同一分佈。對測試樣本x，令y_D為x在資料集中的標記，y為x的真實標記，f(x;D)為訓練集D上學得模型f在x上的預測輸出。以為迴歸任務為例，學習演算法的期望預測為：

正好分解為：偏差、方差和噪聲之和。

偏差度量了學習演算法的期望預測與真實結果的偏離程度，即刻畫了學習演算法本身的擬合能力；方差度量了同樣大小的訓練集的電動所導致的學習效能的變化，即刻畫了資料擾動所造成的影響；噪聲則表達了當前任務上任何學習演算法所能達到的期望泛化誤差的下界，即刻畫了學習問題本身的難度。偏差-分差分解說明，泛化效能是由演算法的能力、資料的充分性以及學習任務本身的難度所共同決定的。給定學習任務，為取得較好的泛化效能，需使偏差較小，即能否重複擬合數據，並使方差較小，即使資料擾動產生的影響小。

然而，偏差和方差是有衝突的，稱為偏差-方差窘境（bias-variance dilemma）。給定學習任務並假定學習演算法的訓練程度，在訓練不足時，學習器的擬合能力不夠強，訓練資料的擾動不足以使學習器產生顯著變化，此時偏差主導泛化錯誤率；隨著訓練程度的加深，學習器的擬合能力逐漸增強，訓練資料所發生的擾動漸漸被學習器學到，方差逐漸主導了泛化錯誤率；在訓練程度充足後，學習器的擬合能力已非常強，訓練資料發生的輕微擾動都會導致學習器發生顯著變化，若訓練資料自身的、非全域性的特性被學習器學到了，將發生過擬合。