一個小測試，測試寫的函式對不對

首先是初始化

    input_size = 4
    hidden_size = 10
    num_classes = 3
    num_inputs = 5

    def init_toy_model():
      np.random.seed(0)
      return TwoLayerNet(input_size, hidden_size, num_classes, std=1e-1)

    def init_toy_data():
      np.random.seed(1)
      X = 10 * np.random.randn(num_inputs, input_size)
      y = np.array([0
 
, 1, 2, 2, 1])
      return X, y

    net = init_toy_model()
    X, y = init_toy_data()
    print X.shape, y.shape

初始化

class TwoLayerNet(object):
          def __init__(self, input_size, hidden_size, output_size, std=1e-4):
        """
        Initialize the model. Weights are initialized to small random values and
        biases are initialized to zero. Weights and biases are stored in the
        variable self.params, which is a dictionary with the following keys:

        W1: First layer weights; has shape (D, H)
        b1: First layer biases; has shape (H,)
        W2: Second layer weights; has shape (H, C)
        b2: Second layer biases; has shape (C,)

        Inputs:
        - input_size: The dimension D of the input data.
        - hidden_size: The number of neurons H in the hidden layer.
        - output_size: The number of classes C.
        """
 

        self.params = {}
        self.params['W1'] = std * np.random.randn(input_size, hidden_size)
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = std * np.random.randn(hidden_size, output_size)
        self.params['b2'] = np.zeros(output_size)

對於W1的維數，即將輸入樣本的個數每個分配一個權重，最後輸出相當於是hidden_size個分數，然後這些分數和啟用函式相比較，b1應該是比較的閾值吧（自己覺得），有些分數就不會起作用。這樣得到處理後的分數，在與W2相乘，與啟用函式相比較，可以看到，W2輸出是output_size，也就是說，輸出的分數和類別數一樣，即最終的分數。這裡初始化這四個引數的意思大概就是這樣子。

X的大小X.shape = (5, 4)
y的大小y.shape = (5, )
net.params[‘W1’].shape = (4, 10)
net.params[‘b1’].shape = (10, )
net.params[‘W2’].shape = (10, 3)
net.params[‘b2’].shape = (3, )
知道了維數關係，也就清楚了是 X*W 而不是 W*X，這個按實際去寫，不要硬記。

計算loss和grad

def loss(self, X, y=None, reg=0.0):
    """
    Compute the loss and gradients for a two layer fully connected neural network.

    Inputs:
    - X: Input data of shape (N, D). Each X[i] is a training sample.
    - y: Vector of training labels. y[i] is the label for X[i], and each y[i] is
      an integer in the range 0 <= y[i] < C. This parameter is optional; if it
      is not passed then we only return scores, and if it is passed then we
      instead return the loss and gradients.
    - reg: Regularization strength.

    Returns:
    If y is None, return a matrix scores of shape (N, C) where scores[i, c] is
    the score for class c on input X[i].

    If y is not None, instead return a tuple of:
    - loss: Loss (data loss and regularization loss) for this batch of training
      samples.
    - grads: Dictionary mapping parameter names to gradients of those parameters
      with respect to the loss function; has the same keys as self.params.
    """
    # Unpack variables from the params dictionary
    W1, b1 = self.params['W1'], self.params['b1']
    W2, b2 = self.params['W2'], self.params['b2']
    N, D = X.shape

    # Compute the forward pass
    scores = None
    # Perform the forward pass, computing the class scores for the input.
    # score.shape (N, C).
    h_output = np.maximum(0, X.dot(W1) + b1)  # (N,D) * (D,H) = (N,H)
    scores = h_output.dot(W2) + b2

    # If the targets are not given then jump out, we're done
    if y is None:
      return scores

    # Compute the loss
    loss = None

    #Finish the forward pass, and compute the loss. 
    shift_scores = scores - np.max(scores, axis=1).reshape(-1, 1)
    softmax_output = np.exp(shift_scores) / np.sum(np.exp(shift_scores), axis=1).reshape(-1, 1)
    loss = -np.sum(np.log(softmax_output[range(N), list(y)]))
    loss /= N
    loss += 0.5 * reg * (np.sum(W1 * W1) + np.sum(W2 * W2))

    # Backward pass: compute gradients
    grads = {}

    # Compute the backward pass, computing the derivatives of the weights #
    # and biases. Store the results in the grads dictionary. For example,       #
    # grads['W1'] should store the gradient on W1, and be a matrix of same size #
    dscores = softmax_output.copy()
    dscores[range(N), list(y)] -= 1
    dscores /= N
    grads['W2'] = h_output.T.dot(dscores) + reg * W2
    grads['b2'] = np.sum(dscores, axis=0)

    dh = dscores.dot(W2.T)
    dh_ReLu = (h_output > 0) * dh
    grads['W1'] = X.T.dot(dh_ReLu) + reg * W1
    grads['b1'] = np.sum(dh_ReLu, axis=0)
    return loss, grads

得分scores的計算,由之前權重W和輸入X的shape可知，

h_output = np.maximum(0, X.dot(W1) + b1) #第一層網路，啟用函式為max().
scores = h_output.dot(W2) + b2 #第二層網路，最後得到每個樣本的分數

損失loss的計算，這裡用的是softmax的損失函式，所以，要先減去最大值，歸一化，達到數值穩定。最後取了平均並且加了1/2的正則化項。

shift_scores = scores - np.max(scores, axis=1).reshape(-1, 1) #為了數值穩定
softmax_output = np.exp(shift_scores) / np.sum(np.exp(shift_scores), axis=1).reshape(-1, 1)#算了所有的 分數/sum
loss = -np.sum(np.log(softmax_output[range(N), list(y)])) #損失是正確的分類的分數/sum
loss /= N #compute average
loss += 0.5 * reg * (np.sum(W1 * W1) + np.sum(W2 * W2))#加正則項，這些可以參考之前的softmax

對於梯度的計算，對分類正確的Wyi分類器求導要多一個-Xi（具體求導可以參考上篇softmax部落格），所以這是下面第三行-1的原因。但是為什麼沒有乘以X呢(⊙o⊙)?，求解答
反向傳播計算線路參考圖

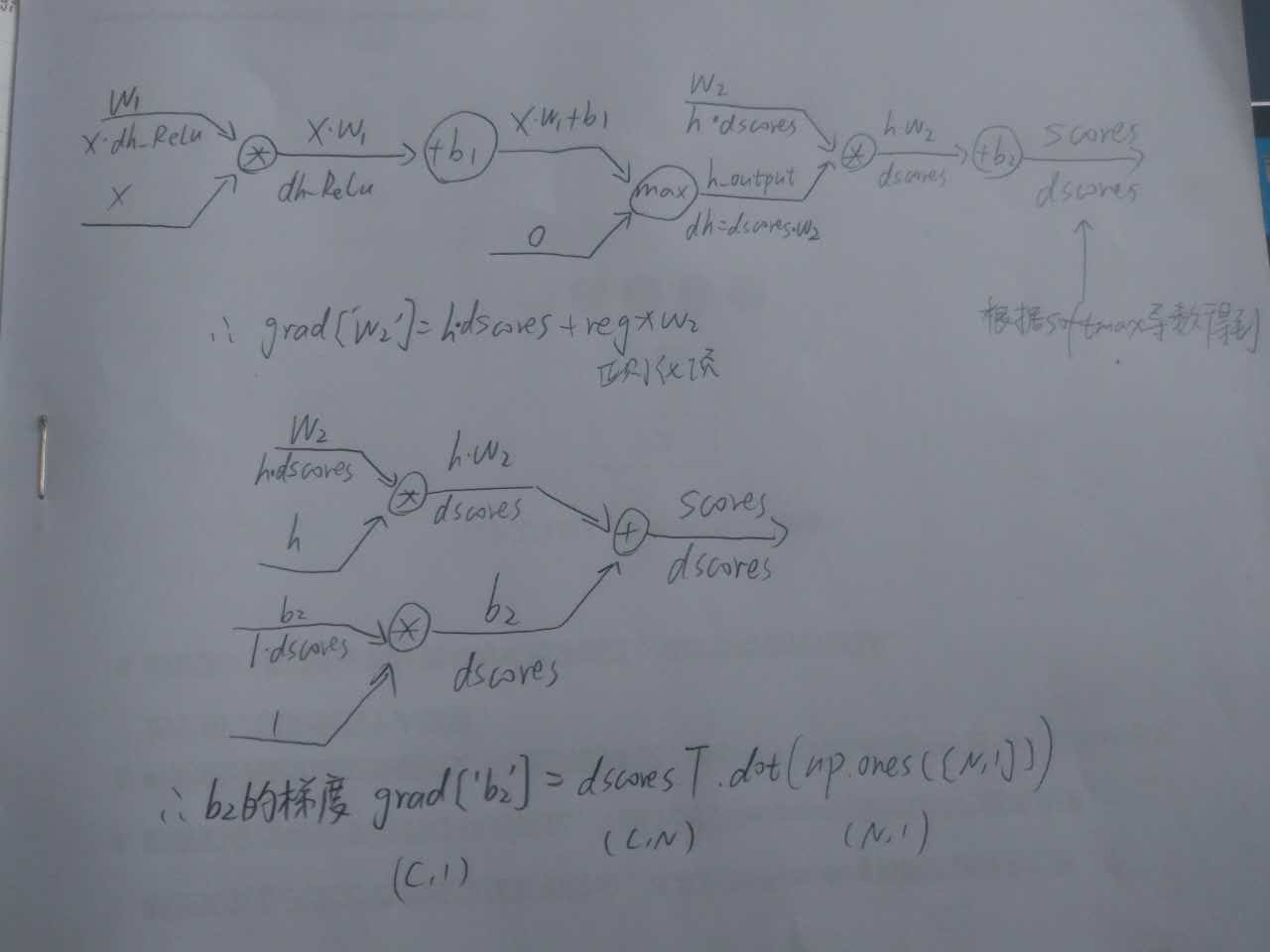
具體對應的程式碼

    grads = {}
    dscores = softmax_output.copy()
    dscores[range(N), list(y)] -= 1
    dscores /= N
    grads['W2'] = h_output.T.dot(dscores) + reg * W2
    grads['b2'] = np.sum(dscores, axis=0)
    dh = dscores.dot(W2.T)
    dh_ReLu = (h_output > 0) * dh
    grads['W1'] = X.T.dot(dh_ReLu) + reg * W1
    grads['b1'] = np.sum(dh_ReLu, axis=0)

最後的測試結果，和提供的正確資料幾乎一致

W1 max relative error: 3.561318e-09
W2 max relative error: 3.440708e-09
b2 max relative error: 4.447625e-11
b1 max relative error: 2.738421e-09

訓練

def train(self, X, y, X_val, y_val,
            learning_rate=1e-3, learning_rate_decay=0.95,
            reg=1e-5, num_iters=100,
            batch_size=200, verbose=False):
    """
    Train this neural network using stochastic gradient descent.

    Inputs:
    - X: A numpy array of shape (N, D) giving training data.
    - y: A numpy array f shape (N,) giving training labels; y[i] = c means that
      X[i] has label c, where 0 <= c < C.
    - X_val: A numpy array of shape (N_val, D) giving validation data.
    - y_val: A numpy array of shape (N_val,) giving validation labels.
    - learning_rate: Scalar giving learning rate for optimization.
    - learning_rate_decay: Scalar giving factor used to decay the learning rate
      after each epoch.
    - reg: Scalar giving regularization strength.
    - num_iters: Number of steps to take when optimizing.
    - batch_size: Number of training examples to use per step.
    - verbose: boolean; if true print progress during optimization.
    """
    num_train = X.shape[0]
    iterations_per_epoch = max(num_train / batch_size, 1)

    # Use SGD to optimize the parameters in self.model
    loss_history = []
    train_acc_history = []
    val_acc_history = []

    for it in xrange(num_iters):
      X_batch = None
      y_batch = None

      # Create a random minibatch of training data and labels, storing  #
      # them in X_batch and y_batch respectively.                             #

      idx = np.random.choice(num_train, batch_size, replace=True)
      X_batch = X[idx]
      y_batch = y[idx]

      # Compute loss and gradients using the current minibatch
      loss, grads = self.loss(X_batch, y=y_batch, reg=reg)
      loss_history.append(loss)

       # Use the gradients in the grads dictionary to update the         #
      # parameters of the network (stored in the dictionary self.params)      #
      # using stochastic gradient descent. You'll need to use the gradients   #
      # stored in the grads dictionary defined above.                         #
     self.params['W2'] += - learning_rate * grads['W2']
      self.params['b2'] += - learning_rate * grads['b2']
      self.params['W1'] += - learning_rate * grads['W1']
      self.params['b1'] += - learning_rate * grads['b1']

      if verbose and it % 100 == 0:
        print 'iteration %d / %d: loss %f' % (it, num_iters, loss)

      # Every epoch, check train and val accuracy and decay learning rate.
      if it % iterations_per_epoch == 0:
        # Check accuracy
        train_acc = (self.predict(X_batch) == y_batch).mean()
        val_acc = (self.predict(X_val) == y_val).mean()
        train_acc_history.append(train_acc)
        val_acc_history.append(val_acc)

        # Decay learning rate
        learning_rate *= learning_rate_decay

    return {
      'loss_history': loss_history,
      'train_acc_history': train_acc_history,
      'val_acc_history': val_acc_history,
    }

訓練基本和之前的softmax和svm一樣，取小樣本，計算損失和梯度，用SGD更新W和b（在svm中，W增加了一列，放b）。
最後的幾句程式碼，計算了預測準確率，並且學習率在不停的減小。

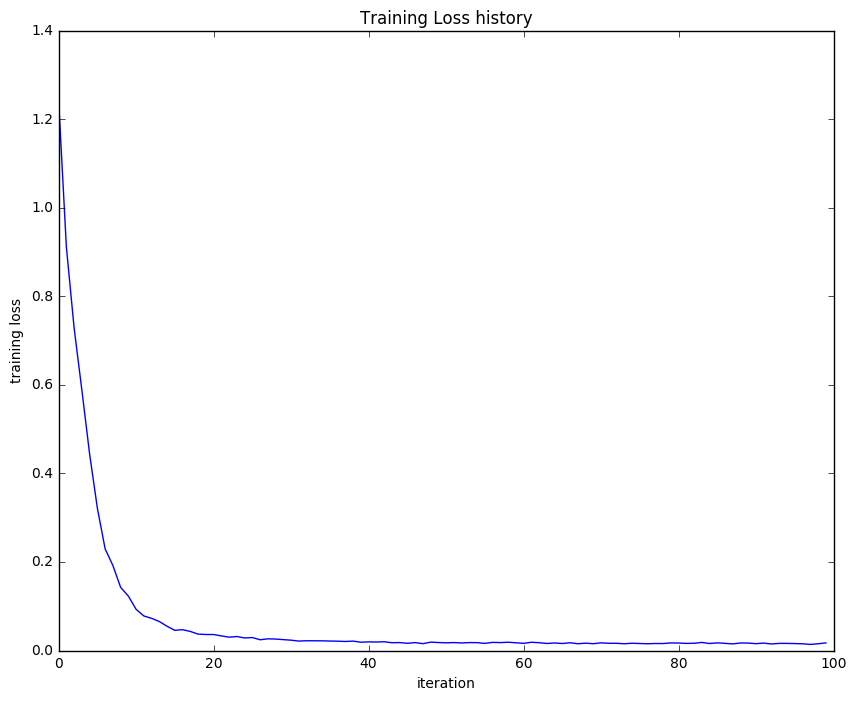
畫出loss_history與迭代次數的曲線，可以看到20次後loss基本不變。

開始用CIFAR10資料實戰

測試小例子很成功呀，是時候開始用CIFAR10資料來實驗。

    input_size = 32 * 32 * 3
    hidden_size = 50
    num_classes = 10
    net = TwoLayerNet(input_size, hidden_size, num_classes)

    # Train the network
    stats = net.train(X_train, y_train, X_val, y_val,
            num_iters=1000, batch_size=200,
            learning_rate=1e-4, learning_rate_decay=0.95,
            reg=0.5, verbose=True)

    # Predict on the validation set
    val_acc = (net.predict(X_val) == y_val).mean()
    print 'Validation accuracy: ', val_acc

輸出結果

iteration 0 / 1000: loss 2.302954
iteration 100 / 1000: loss 2.302550
iteration 200 / 1000: loss 2.297648
iteration 300 / 1000: loss 2.259602
iteration 400 / 1000: loss 2.204170
iteration 500 / 1000: loss 2.118565
iteration 600 / 1000: loss 2.051535
iteration 700 / 1000: loss 1.988466
iteration 800 / 1000: loss 2.006591
iteration 900 / 1000: loss 1.951473
Validation accuracy: 0.287
訓練集的準確率只有28.7%，不太理想呀

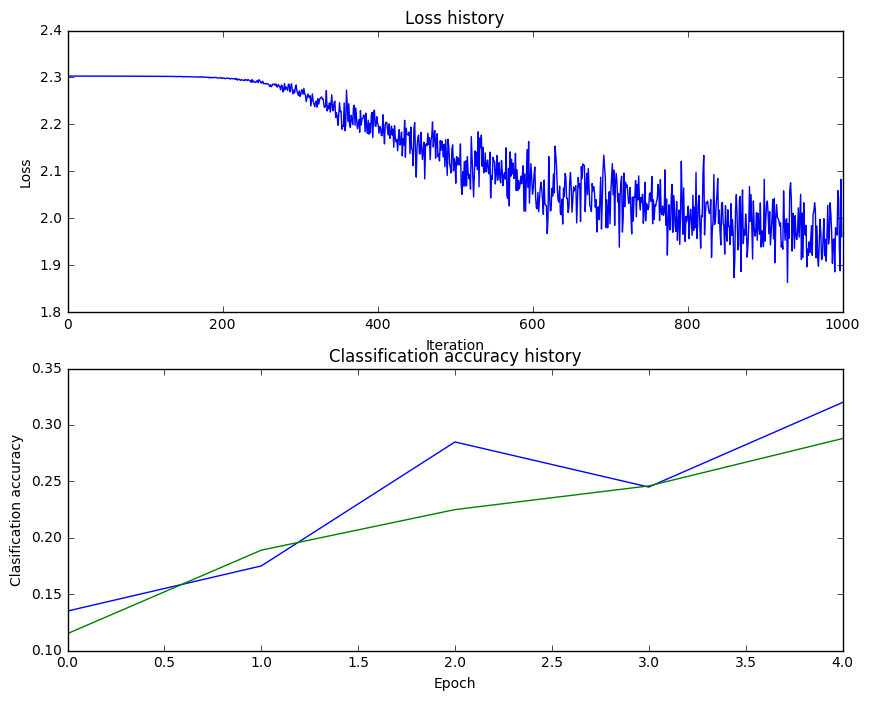
藍線為 train_acc_history，綠線為 val_acc_history

hidden_size = [75, 100, 125]
learning_rates = np.array([0.7, 0.8, 0.9, 1, 1.1])*1e-3
regularization_strengths = [0.75, 1, 1.25]
hs 100 lr 1.100000e-03 reg 7.500000e-01 val accuracy: 0.502000
best validation accuracy achieved during cross-validation: 0.502000
用了三層for迴圈，硬生生找了三個較好的引數，準確率達到了50.2%

hint裡提示用PCA降維，adding dropout, 或者adding features to the solver來到達更好的效果，這些先放著以後試吧（加粗防忘記）

參考

(對了如果想儲存網頁內容，可以用chrome瀏覽器，右鍵列印，儲存為pdf，可以選擇儲存的頁數，再打印出來看，對著電腦看眼睛吃不消了)