Lecture 7  Training Neural Networks 2

課堂筆記參見：https://zhuanlan.zhihu.com/p/21560667?refer=intelligentunit

本節課主要講述比較常用的優化演算法，正則化方法以及遷移學習。 

一、        優化：

隨機梯度下降演算法是有一些問題的，如圖所示，如果目標類似於山坡的最低點，而我們的權重方向W1,W2正好一個豎直，一個水平，對應海森矩陣的最大奇異值和最小奇異值，那麼Loss將會對水平更新非常不敏感。這是我們的SGD演算法會有什麼表現呢？就像如圖所示的之字形軌跡一樣，一遍遍地越過等高線而不能做到沿著曲面下降。因為SGD演算法是沿著超平面上下降最快的方向走的，這個方向可能並沒有指向最優點。這張圖中下降最快的方向明顯是豎直方向，水平方向對Loss的貢獻度低導致水平方向基本不移動，這就導致軌跡總是在上下跳動而並沒有向最優點顯著移動。

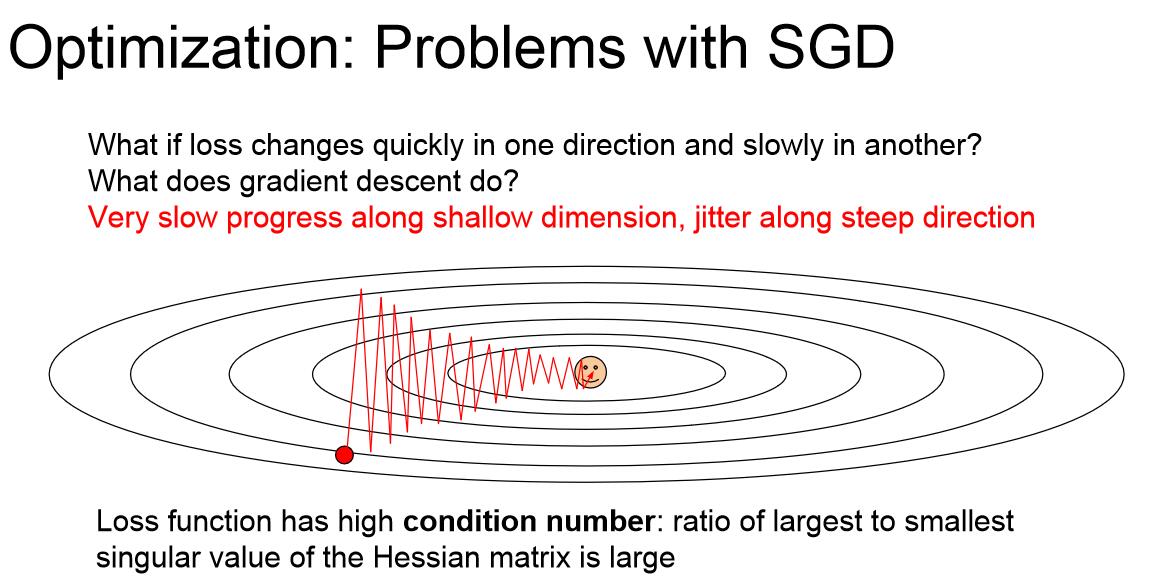
SGD的第二個問題是容易陷入區域性極小值。另外對於鞍點（斜率為0）來說，SGD同樣會導致函式卡在這一點。在高維問題中，鞍點意味著在當前點上某些方向的損失會增加，某些方向的損失會減小，這種情況在你的引數非常多時是很常見的，而區域性極小值意味著在所有方向上行進損失都會增加，在高維網路中這種情況反而並不常見。問題更多地出現在鞍點上。在鞍點附近，梯度值非常小，所以梯度更新會變得異常緩慢。

第三個SGD的問題來源於Stochastic，我們通常不用全部資料來計算Loss，因為每一次迭代都意味著巨大的計算量，我們往往在每一個小batch上計算Loss和梯度作為估計值，這時如果我們在網路中加入隨機噪聲，我們會發現隨機噪聲的影響會變得很大，因為梯度下降的隨機性可能會使選擇出來的資料中噪聲成分偏多。在使用所有資料時，這種隨機性依然會導致結果受到網路中噪聲的影響。

這三個問題都能用一個簡單的技巧解決，就是在SGD中加入動量項。

當然這種動量法並不是純粹物理意義上的動量，而是說梯度更新項會在一定程度上保持原有的趨勢（不再是SGD的任意變化），ρ可以理解為是摩擦係數，表示對原梯度值項的衰減因子。這個策略基本解決了我們剛才討論的所有問題。速度項一般初始化為0。

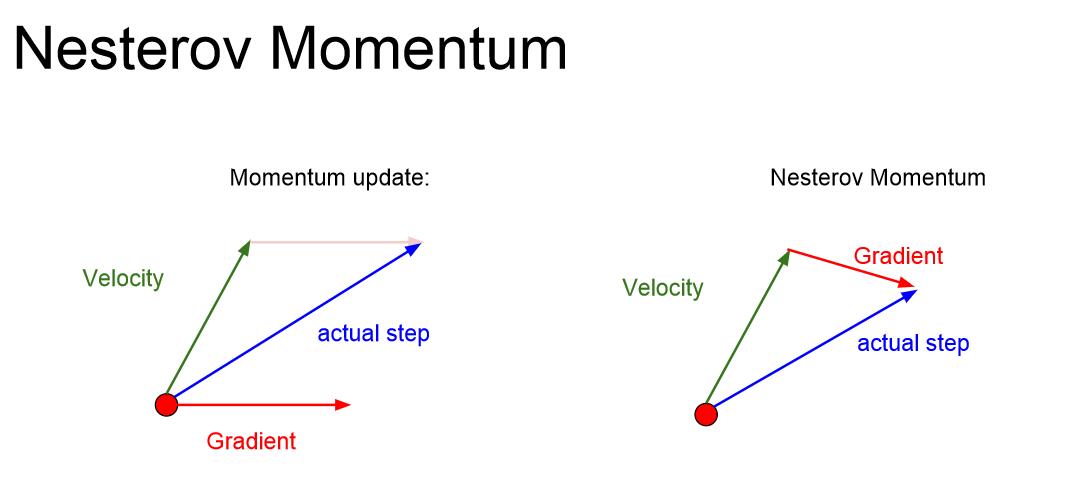
另一種動量方法的思路是Nesterov Momentum:

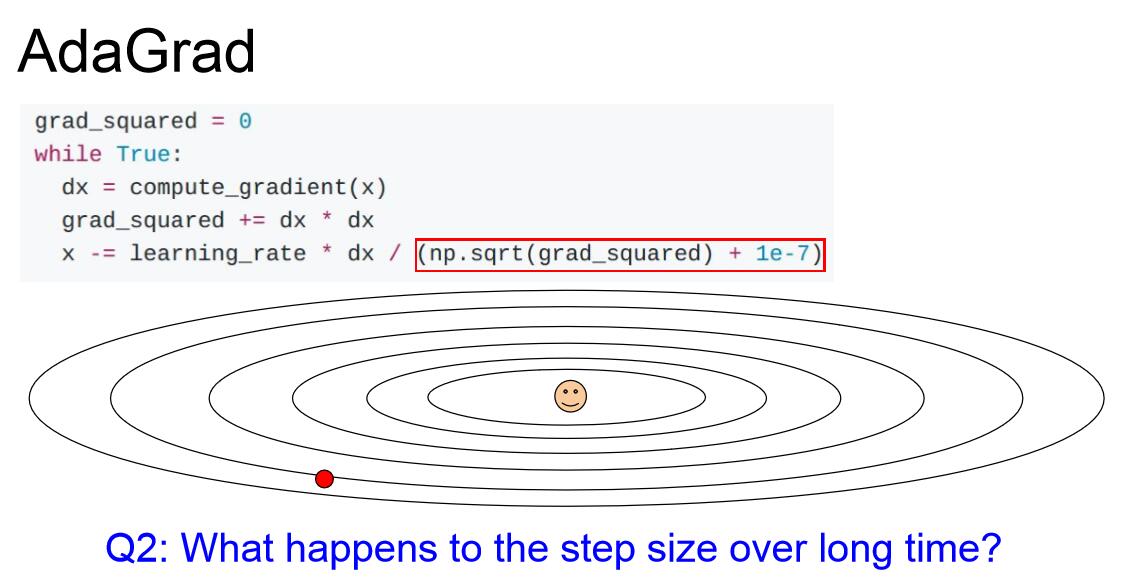
另一種優化思路是斯坦福的John Duchi教授提出的AdaGrad，其核心思想是計算每一步梯度的平方，累加求和，並讓引數更新的時候除以這個平方和的平方根。這樣如果我們有如上問題二所說的兩個W方向，豎直方向得到的大梯度值會使實際的梯度更新較小，而水平方向上的小梯度值會使實際的梯度更新較大，從而解決了問題二。但是隨著迭代次數增加，步長會越來越小，這在凸函式逼近中是一個優勢，但是非凸函式情形很容易被區域性極小值困住。

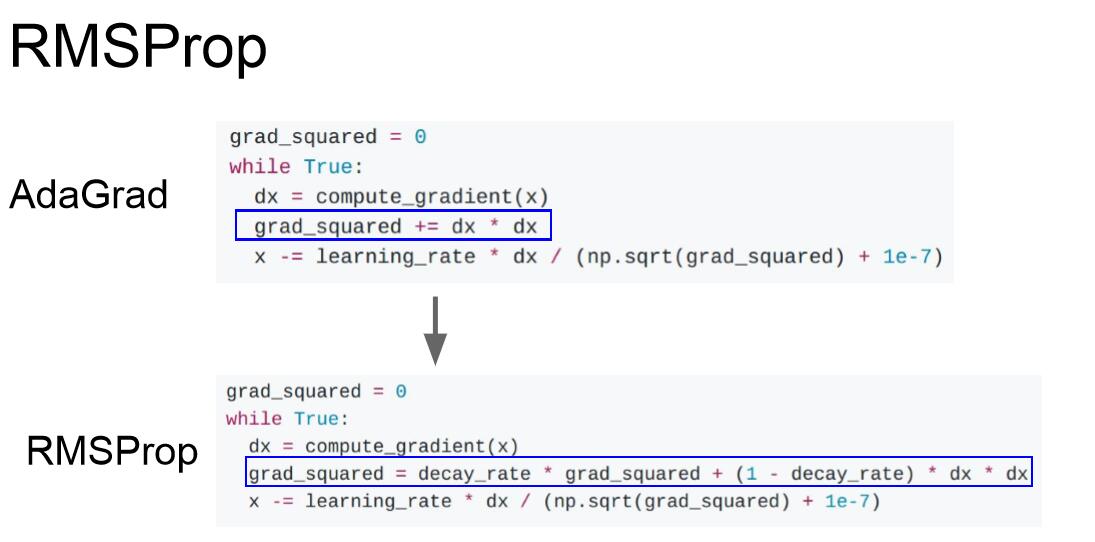
AdaGrad的一個變體是RMSProp，引入了衰減率decay_rate，衰減率通常為0.9或者0.99，用以解決隨著迭代次數增加而使步長減小的問題。但是訓練速度可能會變慢。

Adam（初期）演算法是Momentum 和 RMSProp的結合。相當於在dx，x之間加入了兩個變換，dx-first_moment-second_moment-x，分別引入了動量和RMSProp，

然而，如果我們看第一步就會發現，初始值第一、二動量都是零，beta2是0.9或者0.99，所以第一次更新後，第二動量依然很小，這就導致第一步的步長很大。

完善後的Adam引入了偏置校正項，以避免一開始的大步長。Adam幾乎對於所有問題表現都很好，所以可以作為我們的預設優化演算法。上圖中有初始設定值的推薦。

Tips：學習率的設定：

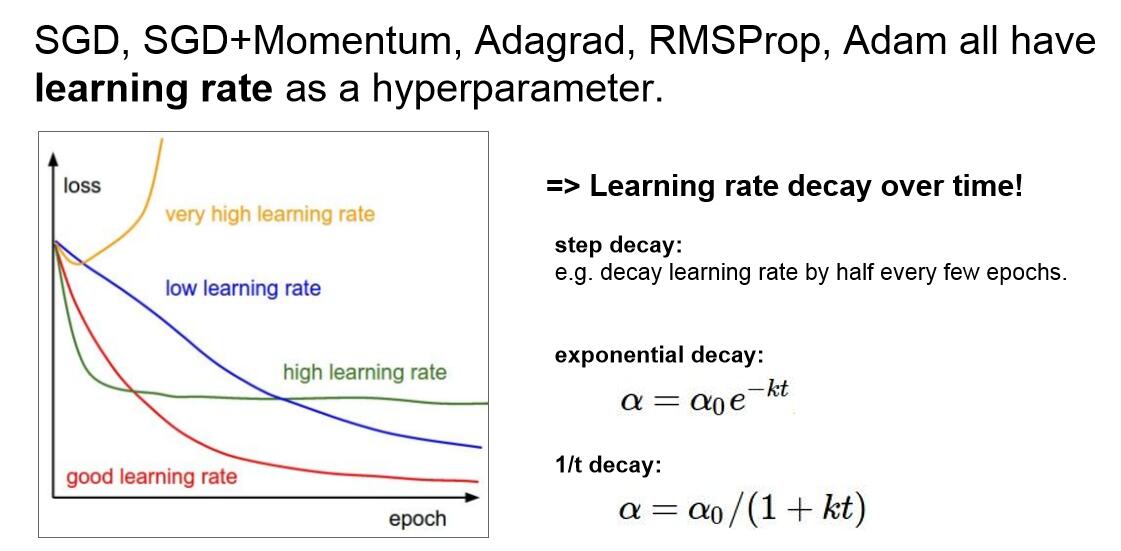
我們之前所講的都是一階求導的梯度更新，如果你結合一維變數的二階求導，然後做一個二階泰勒逼近，就可以用一個二次函式逼近我們的函式，可以直接跳到函式點的對應最小值點，這就是二階優化的思想。將問題拓展到多維變數，就是牛頓步長的概念。我們要做的是計算海森矩陣（二階偏導矩陣），求這個矩陣的逆，以找到二次逼近後的最小值。這個演算法就沒有學習率的概念了，但是實際運用中我們也會用到學習率，因為這個演算法也不是那麼完美。

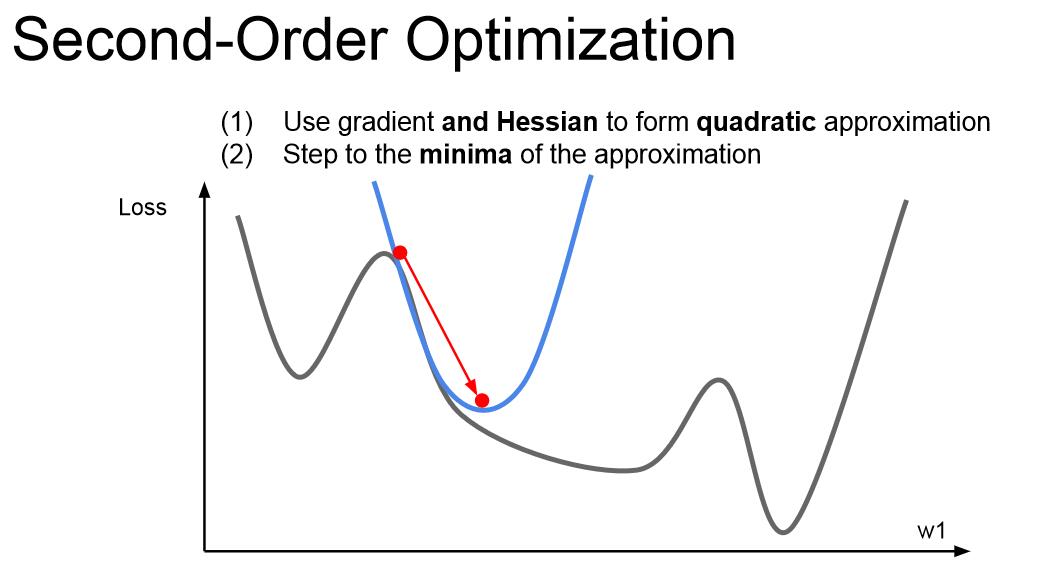
不過，這個演算法不適合深度學習，因為海森矩陣是N*N的矩陣（N是網路引數的數量），記憶體是無法存下這個矩陣的。所以人們經常使用擬牛頓法來替代牛頓法，不直接去求完整的Hessian矩陣的逆，而是去逼近這個矩陣的逆，常用的是低階逼近。

L-BFGS就是一個二階優化器，採用了Hessian矩陣的二階逼近，不過對很多深度學習問題不適用，因為這種逼近演算法對隨機情況的處理不是那麼好，在非凸問題表現也不是很好。當你的網路引數不是很多，隨機性也不是很強的時候，L-BFGS有時候會發揮好的效果。

如何減小訓練集和驗證集Loss的差距呢？一個簡單的方法是模型整合（Model Ensembels），相比於訓練一個模型，我們選擇從不同的隨機初始值上訓練10個不同的模型，然後在這樣的10個模型上執行測試資料，然後平均預測結果，這樣可以在一定程度上緩解過擬合，從而提高預測結果。如果發揮一定的想象力，我們並不一定需要真的去訓練10個不同的模型，而是在訓練過程中獲取模型的快照（snapshots），來進行整合學習。在測試階段，我們將這些快照預測結果做平均。

另外一個trick是我們可以對不同訓練時刻的模型引數求指數衰減平均值，從而得到一個比較平滑的整合模型，這叫做Polyak averaging，但事實上並不常用。