51nod 1113 (矩陣快速冪講解)
阿新 • • 發佈:2019-01-25
快速冪:快速冪是一種十分快速的解決冪運算的方法。能把時間複雜度從n降到logn。十分高效的演算法。大致思路是這樣的16 = 2 * 2 * 2 * 2.是四個2相乘。我們計算時可以把2兩兩結合 就變成16 = (2 * 2) * (2 * 2)= 4 * 4 變成了兩個4相乘。.這樣就降低了運算的次數。如果是32 = 2 * 2 * 2 * 2 * 2當相乘的個數為5個 ,為奇數時。沒有辦法兩兩結合,我們可以把他單獨拉出計算。
實現程式碼如下:
int quick_pow(int a,int b){ int ret = 1; while(b){ if(b&1) ret = ret * a; a = a * a; b >>= 1; } return ret; }
其中牽扯到一點二進位制運算。如b&1 是判斷b為奇數還是偶數。 b>>=1 是b/2的意思。
要講矩陣快速冪。那必須先說一說什麼是矩陣。但是矩陣又不是這個重點,我就簡述一下矩陣的運算把。
簡單的說矩陣就是二維陣列,數存在裡面,矩陣乘法的規則:A*B=C
其中c[i][j]為A的第i行與B的第j列對應乘積的和,即: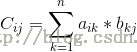
公式很簡單。簡單一句話就是,新矩陣的第I行第j列 是第一個矩陣的i行的每一個元素乘上另一個矩陣的j列每一個元素的總和。
矩陣快速冪:當多相同個矩陣相乘時和數字的冪運算差不多。也可以用矩陣來優化這個運算次數,程式碼如下:
如果理解快速冪,那麼理解矩陣快速冪也非常容易,但是快速冪的應用不止如此。這只是模板介紹。#include<bits/stdc++.h> using namespace std; typedef long long ll; const int maxn = 110; const int mod = 1e9+7; int n; struct mat{ int m[maxn][maxn]; }unit; mat operator * (mat a,mat b){ mat ret ; ll x; for(int i =0 ; i < n ; i++){ for(int j = 0 ; j < n ; j++){ x = 0 ; for(int k = 0 ; k < n ; k ++) x += ((ll)a.m[i][k] * (ll)b.m[k][j]) % mod; ret.m[i][j] = x % mod; } } return ret; } void init_unit(){ for(int i = 0 ; i < maxn ; i ++) unit.m[i][i] = 1; return ; } mat pow_unit(mat a,ll n){ mat ret = unit; while(n){ if(n&1) ret = ret*a ; a = a * a; n >>= 1; } return ret; } int main(){ ll x; init_unit(); while(cin >> n >> x){ mat a; for(int i = 0 ; i < n ; i ++){ for(int j = 0; j < n ;j ++) cin >> a.m[i][j]; } a = pow_unit(a,x); for(int i = 0 ; i < n ; i ++){ for(int j = 0 ; j < n ; j ++){ if( j + 1 == n) cout << a.m[i][j] << endl; else cout <<a.m[i][j] <<" "; } } } return 0; }

