基本介紹

網上看了很多關於求解一個有向圖的強連通分支個數的演算法，其中最著名的莫過於：
Kosaraju 演算法

看的比較暈！

過程如下：
1。 建立一個空的棧 S，並做一次 DFS 遍歷。在 DFS 遍歷中，當在遞迴呼叫 DSF 訪問鄰接頂點時，將當前頂點壓入棧中；
2。 置換圖（Transpose Graph）；
3。 從棧 S 中逐個彈出頂點 v，以 v 為源點進行 DFS 遍歷。從 v 開始的 DFS 遍歷將輸出 v 關聯的強連通分支。直到S中元素全部彈出。

演算法原理理解

先說一下強連通分支：
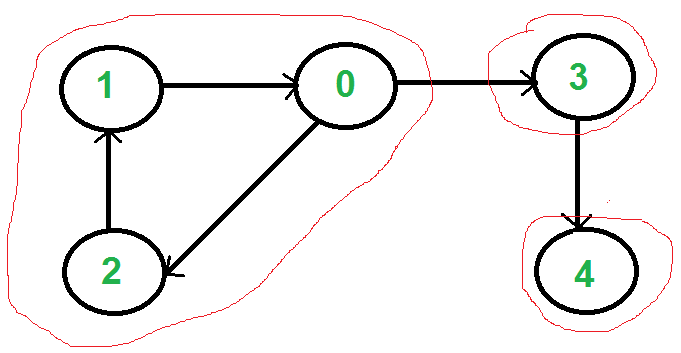
比如上圖中1，0，2屬於一個強連通分支。
講述之前先說一個自己理解的重要基本知識點：

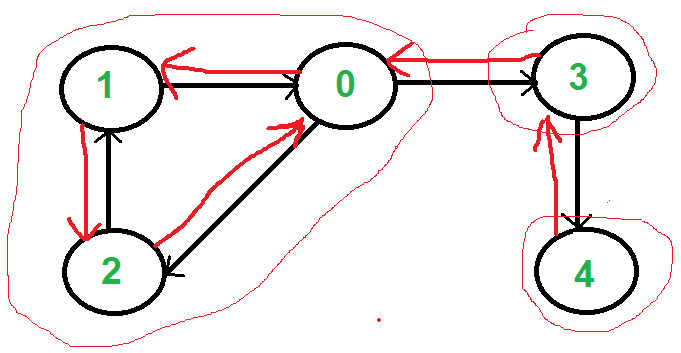
在一個有向圖中，如果s和v連線（之間連著路，但並不表示s到v可達或者v到s可達，只是說連著）。將這個有向圖的所有路徑取反，在鄰接矩陣中對應著矩陣轉置，如果： s能夠抵達v，那麼：在原圖中，一定是v能夠抵達s。
這個結論很明顯，明顯的不需要證明。然而就是這麼一個結論，是理解本演算法的最關鍵的一點。

很明顯在第一步DFS過程中，依次入棧的元素是：
1，2，4，3，0。
這個不解釋！我之前一直除錯不對的原因是把入棧元素程式碼放在最前面了。

int DFS_1(int *map, int v,bool *visited,int N, stack<int> &S)
{
    visited[v] = 1
 
;//v被訪問過
    //S.push(v);//入棧操作錯誤！
    for (int i = 0; i < N; i++)
    {
        if (!visited[i] && map[v*maxnum+i])//二維陣列訪問
            DFS_1(map, i, visited, N,S);
    }
    S.push(v);//這個入棧操作要放到這，才是對的
    return 0;
}

那麼在原圖反轉之後

第一個出棧的是0，然後對它DFS，只要0能夠遍歷到的，都屬於0所代表的強連通分支。比如0能訪問1，則在原圖中1能到0，又因為0能到1，所以0，1屬於 一個強連通分支中。
上述理解似乎簡單了點，因為沒說一個很重要的點，那就是在第一次DFS入棧操作中，如果一個頂點能夠遍歷的都遍歷完了，包括其子頂點也遍歷完了，那麼該頂點入棧。此時該頂點以下的元素（棧底）都是該頂點能夠訪問到的，至於以後入棧的元素，不管他，至少該頂點不能訪問到。所以在第二次DFS過程中，該頂點能夠遍歷到的，只在其底部的頂點中找，和它上面的沒關係。這就保證了該頂點第二次DFS能夠得到屬於它的強連通分支。

上面的有點囉嗦，不過有助於理解。

演算法除錯起來一直被一個點困擾著，後來再次理解演算法時才發現。果然理解很重要！

程式碼

#include<iostream>
#include<stack>
#include<fstream>
#define maxnum 100
using namespace std;
int main()
{
    int kosaraju(int *map, int *nmap, int N);
    int N, M;
    int map[maxnum][maxnum];
    int nmap[maxnum][maxnum];
    bool visited[maxnum];//表示頂點i是否被訪問過

    ifstream in("input.txt");
    in >> N >> M;//讀取頂點數和邊數
    memset(map, 0, sizeof(map));
    memset(nmap, 0, sizeof(nmap));
    memset(visited, 0, sizeof(visited));
    int a,b;
    for (int i = 0; i < M; i++)
    {
        in >> a >> b;
        map[a][b] = 1;
        nmap[b][a] = 1;
    }
    int cnt=kosaraju((int *)map, (int *)nmap, N);
    cout << endl;
    cout << "強連通分支個數" <<cnt<< endl;
    return 0;
}
int DFS_1(int *map, int v,bool *visited,int N, stack<int> &S)
{
    visited[v] = 1;//v被訪問過

    for (int i = 0; i < N; i++)
    {
        if (!visited[i] && map[v*maxnum+i])//二維陣列訪問
            DFS_1(map, i, visited, N,S);
    }
    S.push(v);
    return 0;
}
int DFS_2(int *nmap, int v, bool *visited, int N)
{
    visited[v] = 1;//v被訪問過
    for (int i = 0; i < N; i++)
    {
        if (!visited[i] && nmap[v*maxnum + i])
            DFS_2(nmap, i, visited, N);
    }
    return 0;
}

int kosaraju(int *map, int *nmap,int N)
{

    stack<int> S;
    int cnt = 0;
    bool visited[501];
    while (!S.empty())
        S.pop();
    memset(visited, 0, sizeof(visited));
    for (int i = 0; i < N; i++)
    {
        if (!visited[i])
            DFS_1(map, i, visited, N, S);
    }
    memset(visited, 0, sizeof(visited));
    cout << "出棧順序：";
    while (!S.empty())
    {
        int top = S.top();

        if (!visited[top])
        {

            DFS_2(nmap, top, visited, N);
            cnt++;

        }
        cout << top ;
        S.pop();

    }
    return cnt;
}

參考