最小生成樹——Kruskal演算法和Prim演算法
阿新 • • 發佈:2019-01-25
關於圖的幾個概念定義:
- 連通圖:在無向圖中,若任意兩個頂點vi” role=”presentation”>vivi都有路徑相通,則稱該無向圖為連通圖。
- 強連通圖:在有向圖中,若任意兩個頂點vi” role=”presentation”>vivi都有路徑相通,則稱該有向圖為強連通圖。
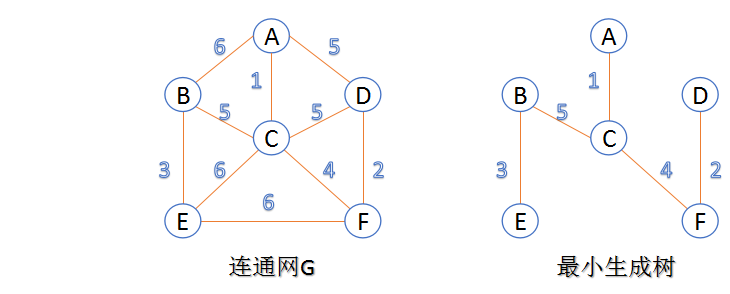
- 連通網:在連通圖中,若圖的邊具有一定的意義,每一條邊都對應著一個數,稱為權;權代表著連線連個頂點的代價,稱這種連通圖叫做連通網。
- 生成樹:一個連通圖的生成樹是指一個連通子圖,它含有圖中全部n個頂點,但只有足以構成一棵樹的n-1條邊。一顆有n個頂點的生成樹有且僅有n-1條邊,如果生成樹中再新增一條邊,則必定成環。
- 最小生成樹:在連通網的所有生成樹中,所有邊的代價和最小的生成樹,稱為最小生成樹。
下面介紹兩種求最小生成樹演算法
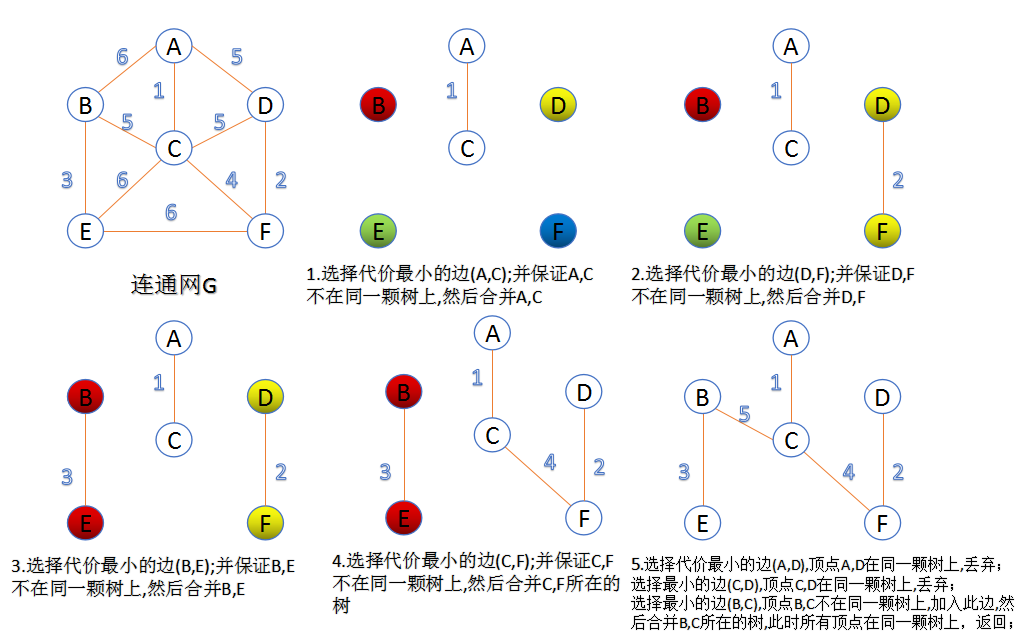
1.Kruskal演算法
此演算法可以稱為“加邊法”,初始最小生成樹邊數為0,每迭代一次就選擇一條滿足條件的最小代價邊,加入到最小生成樹的邊集合裡。
1. 把圖中的所有邊按代價從小到大排序;
2. 把圖中的n個頂點看成獨立的n棵樹組成的森林;
3. 按權值從小到大選擇邊,所選的邊連線的兩個頂點ui,vi” role=”presentation”>ui,viui,vi,應屬於兩顆不同的樹,則成為最小生成樹的一條邊,並將這兩顆樹合併作為一顆樹。
4. 重複(3),直到所有頂點都在一顆樹內或者有n-1條邊為止。
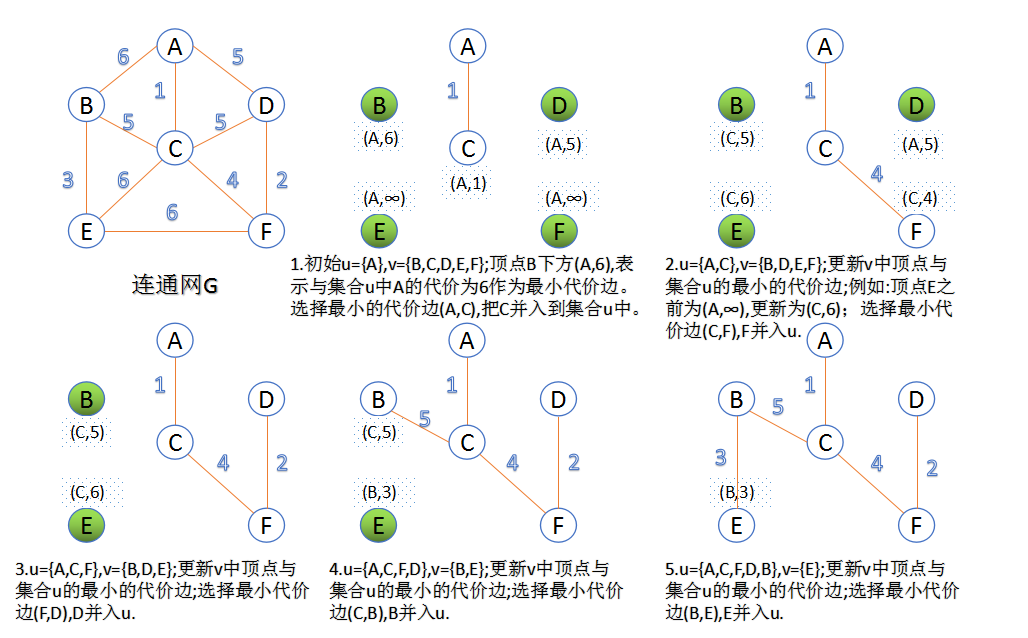
2.Prim演算法
此演算法可以稱為“加點法”,每次迭代選擇代價最小的邊對應的點,加入到最小生成樹中。演算法從某一個頂點s開始,逐漸長大覆蓋整個連通網的所有頂點。
- 圖的所有頂點集合為V” role=”presentation”>VV;
- 在兩個集合u,v” role=”presentation”>u,vu,v併入到集合u中。
- 重複上述步驟,直到最小生成樹有n-1條邊或者n個頂點為止。
由於不斷向集合u中加點,所以最小代價邊必須同步更新;需要建立一個輔助陣列closedge,用來維護集合v中每個頂點與集合u中最小代價邊資訊,:
struct
{
char - 1
- 2
- 3
- 4
- 5
3.完整程式碼
/************************************************************************
CSDN 勿在浮沙築高臺 http://blog.csdn.net/luoshixian099演算法導論--最小生成樹(Prim、Kruskal)2016年7月14日
************************************************************************/
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
#define INFINITE 0xFFFFFFFF
#define VertexData unsigned int //頂點資料
#define UINT unsigned int
#define vexCounts 6 //頂點數量
char vextex[] = { 'A', 'B', 'C', 'D', 'E', 'F' };
struct node
{
VertexData data;
unsigned int lowestcost;
}closedge[vexCounts]; //Prim演算法中的輔助資訊
typedef struct
{
VertexData u;
VertexData v;
unsigned int cost; //邊的代價
}Arc; //原始圖的邊資訊
void AdjMatrix(unsigned int adjMat[][vexCounts]) //鄰接矩陣表示法
{
for (int i = 0; i < vexCounts; i++) //初始化鄰接矩陣
for (int j = 0; j < vexCounts; j++)
{
adjMat[i][j] = INFINITE;
}
adjMat[0][1] = 6; adjMat[0][2] = 1; adjMat[0][3] = 5;
adjMat[1][0] = 6; adjMat[1][2] = 5; adjMat[1][4] = 3;
adjMat[2][0] = 1; adjMat[2][1] = 5; adjMat[2][3] = 5; adjMat[2][4] = 6; adjMat[2][5] = 4;
adjMat[3][0] = 5; adjMat[3][2] = 5; adjMat[3][5] = 2;
adjMat[4][1] = 3; adjMat[4][2] = 6; adjMat[4][5] = 6;
adjMat[5][2] = 4; adjMat[5][3] = 2; adjMat[5][4] = 6;
}
int Minmum(struct node * closedge) //返回最小代價邊
{
unsigned int min = INFINITE;
int index = -1;
for (int i = 0; i < vexCounts;i++)
{
if (closedge[i].lowestcost < min && closedge[i].lowestcost !=0)
{
min = closedge[i].lowestcost;
index = i;
}
}
return index;
}
void MiniSpanTree_Prim(unsigned int adjMat[][vexCounts], VertexData s)
{
for (int i = 0; i < vexCounts;i++)
{
closedge[i].lowestcost = INFINITE;
}
closedge[s].data = s; //從頂點s開始
closedge[s].lowestcost = 0;
for (int i = 0; i < vexCounts;i++) //初始化輔助陣列
{
if (i != s)
{
closedge[i].data = s;
closedge[i].lowestcost = adjMat[s][i];
}
}
for (int e = 1; e <= vexCounts -1; e++) //n-1條邊時退出
{
int k = Minmum(closedge); //選擇最小代價邊
cout << vextex[closedge[k].data] << "--" << vextex[k] << endl;//加入到最小生成樹
closedge[k].lowestcost = 0; //代價置為0
for (int i = 0; i < vexCounts;i++) //更新v中頂點最小代價邊資訊
{
if ( adjMat[k][i] < closedge[i].lowestcost)
{
closedge[i].data = k;
closedge[i].lowestcost = adjMat[k][i];
}
}
}
}
void ReadArc(unsigned int adjMat[][vexCounts],vector<Arc> &vertexArc) //儲存圖的邊代價資訊
{
Arc * temp = NULL;
for (unsigned int i = 0; i < vexCounts;i++)
{
for (unsigned int j = 0; j < i; j++)
{
if (adjMat[i][j]!=INFINITE)
{
temp = new Arc;
temp->u = i;
temp->v = j;
temp->cost = adjMat[i][j];
vertexArc.push_back(*temp);
}
}
}
}
bool compare(Arc A, Arc B)
{
return A.cost < B.cost ? true : false;
}
bool FindTree(VertexData u, VertexData v,vector<vector<VertexData> > &Tree)
{
unsigned int index_u = INFINITE;
unsigned int index_v = INFINITE;
for (unsigned int i = 0; i < Tree.size();i++) //檢查u,v分別屬於哪顆樹
{
if (find(Tree[i].begin(), Tree[i].end(), u) != Tree[i].end())
index_u = i;
if (find(Tree[i].begin(), Tree[i].end(), v) != Tree[i].end())
index_v = i;
}
if (index_u != index_v) //u,v不在一顆樹上,合併兩顆樹
{
for (unsigned int i = 0; i < Tree[index_v].size();i++)
{
Tree[index_u].push_back(Tree[index_v][i]);
}
Tree[index_v].clear();
return true;
}
return false;
}
void MiniSpanTree_Kruskal(unsigned int adjMat[][vexCounts])
{
vector<Arc> vertexArc;
ReadArc(adjMat, vertexArc);//讀取邊資訊
sort(vertexArc.begin(), vertexArc.end(), compare);//邊按從小到大排序
vector<vector<VertexData> > Tree(vexCounts); //6棵獨立樹
for (unsigned int i = 0; i < vexCounts; i++)
{
Tree[i].push_back(i); //初始化6棵獨立樹的資訊
}
for (unsigned int i = 0; i < vertexArc.size(); i++)//依次從小到大取最小代價邊
{
VertexData u = vertexArc[i].u;
VertexData v = vertexArc[i].v;
if (FindTree(u, v, Tree))//檢查此邊的兩個頂點是否在一顆樹內
{
cout << vextex[u] << "---" << vextex[v] << endl;//把此邊加入到最小生成樹中
}
}
}
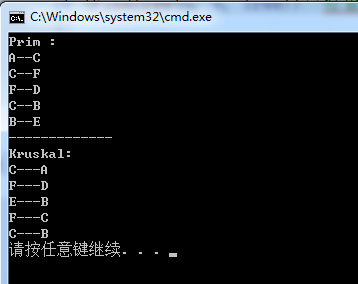
int main()
{
unsigned int adjMat[vexCounts][vexCounts] = { 0 };
AdjMatrix(adjMat); //鄰接矩陣
cout << "Prim :" << endl;
MiniSpanTree_Prim(adjMat,0); //Prim演算法,從頂點0開始.
cout << "-------------" << endl << "Kruskal:" << endl;
MiniSpanTree_Kruskal(adjMat);//Kruskal演算法
return 0;
}- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
Reference:
資料結構–耿國華
演算法導論–第三版