Reinforcement Learning 的核心基礎概念及實現
2013 年倫敦的一家小公司 DeepMind 發表了一篇論文 Playing Atari with Deep Reinforcement Learning 。論文描述瞭如何教會電腦玩 Atari 2600 遊戲(僅僅讓電腦觀察遊戲的每一幀影象和接受遊戲分數的上升作為獎勵訊號)。結果很令人滿意,因為電腦比大多數人類玩家玩的好,而且該模型在沒有任何改變的情況下,學會了玩其他遊戲,並且在三個遊戲中表現比人類玩家好!自此通用人工智慧的話題開始火熱 -- 能夠適應各種負責環境而不僅僅侷限於玩棋類遊戲,而 DeepMind 因此被谷歌看中而被收購。2015 年,DeepMind 又發表了一篇 Human-level control through deep reinforcement learning
自此,在機器學習領域,除了監督學習和非監督學習,強化學習(Reinforcement Learning)也逐漸走進人們的視野。
強化學習
以打磚塊遊戲為例,遊戲中你控制底部的擋板來反彈小球,來清除螢幕上半部分的磚塊。每次你打中磚塊,分數增加,你也得到一個獎勵,而沒有接到小球則會受到懲罰。
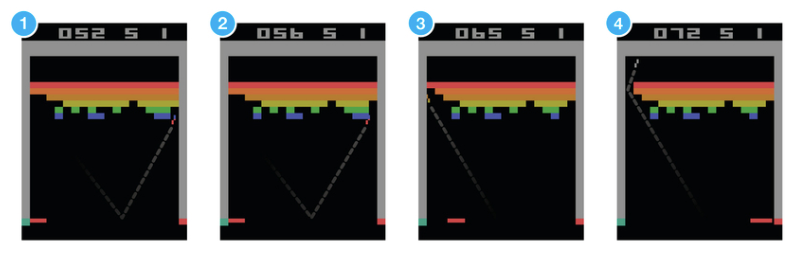
假設讓一個神經網路來玩這個遊戲, 輸入是螢幕影象,輸出將是三個動作:左,右或發射球。很明顯這是一個分類問題,對於每一幀影象,我們計算到到一個動作即可(為螢幕資料分類)。 但是聽起來很簡單,實際上有很多有挑戰性的細節。因為我們當前的動作獎勵有可能是在此之後一段時間獲得的。不像監督學習,對於每一個樣本,都有一個確定的標籤與之對應,而強化學習沒有標籤,只有一個時間延遲的獎勵,而且遊戲中我們往往犧牲當前的獎勵來獲取將來更大的獎勵。因為我們的小球在打到磚塊,獲得獎勵時,事實上擋板並沒有移動,該獎勵是由於之前的一系列動作來獲得的。這就是信用分配問題(Credit Assignment Problem),即當前的動作要為將來獲得更多的獎勵負責。
而且在我們找到一個策略,讓遊戲獲得不錯的獎勵時,我們是選擇繼續堅持當前的策略,還是探索新的策略以求更多的獎勵?這就是探索與開發(Explore-exploit Dilemma)的問題。
強化學習就是一個重要的解決此類問題的模型,它是從我們的人類經驗中總結出來的。在現實生活中,如果我們做某件事獲得獎勵,那麼我們會更加偏向於做這件事。比如你的狗狗早上給你把鞋子叼過來,你對他說 Good dog 並獎勵它,那麼狗狗會更加偏向於叼鞋。而且人類每天在學校的成績、在家來自父母的誇獎、還是工作上的薪水本質上都是在獎勵。
馬爾可夫決策過程 (Markov Decision Process)
那麼如何用數學的方法來解決此類問題呢?最常用的方法就是那此類問題看作一個馬爾可夫決策過程 (Markov Decision Process)。
MDP 中有兩個物件:Agent 和 Environment。
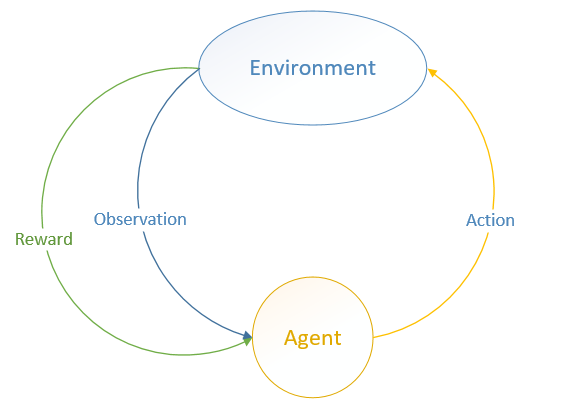
Environment 處於一個特定的狀態(State)(如打磚塊遊戲中擋板的位置、各個磚塊的狀態等),Agent 可以通過執行特定的動作( Actions )(如向左向右移動擋板)來改變 Environment 的狀態, Environment 狀態改變之後會返回一個觀察(Observation)給Agent,同時還會得到一個獎勵(Reward)(可以為負,就是懲罰),這樣 Agent 根據返回的資訊採取新的動作,如此反覆下去。Agent 如何選擇動作叫做策略(Policy)。MDP 的任務就是找到一個策略,來最大化獎勵。
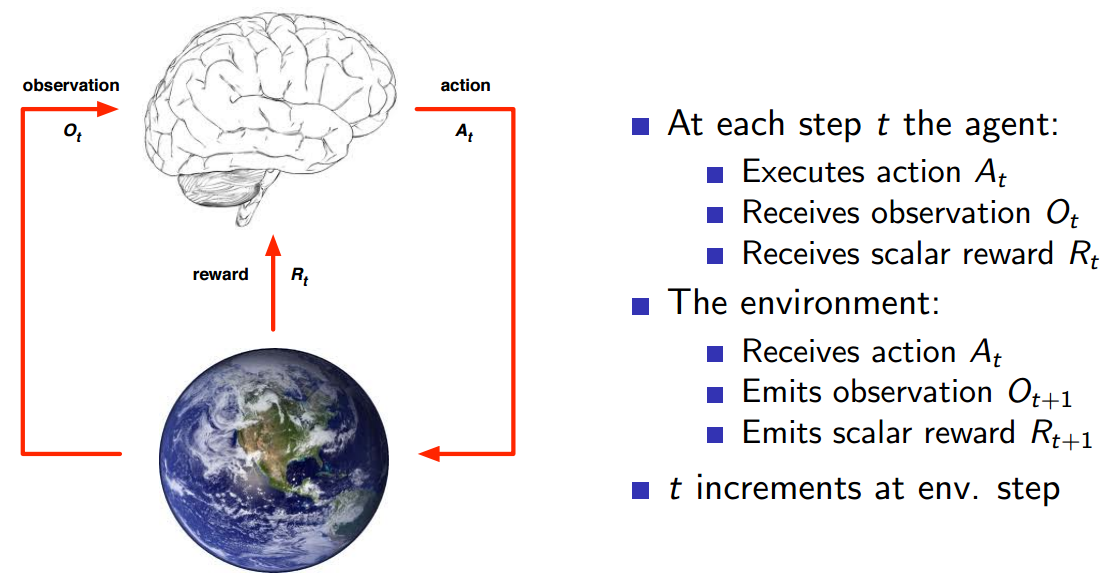
具體的執行步驟如上圖圖所示。注意 State 和 Observation 區別:State 是 Environment 的私有表達,我們往往不知道不會直接到的。在 MDP 中,當前狀態State (Markov state)包含了所有歷史資訊,即將來只和現在有關,與過去無關,因為現在狀態包含了所有歷史資訊。舉個例子,在一個遵循牛頓第二定律的世界裡,我們隨意丟擲一個小球,某一時刻 t 知道了小球的速度和加速度,那麼 t 之後的小球的位置都可以由當前狀態,根據牛頓第二定律計算出來。再舉一個誇張的例子,如果宇宙大爆炸時奇點的狀態已知,那麼以後的所有狀態就已經確定,包括人類進化、我寫這篇文章和你在閱讀這篇文章都是可以根據那一狀態推斷出來的。當然這只是理想狀況,現實往往不會那麼簡單(因為這只是馬爾科夫的一個假設)。只有滿足這樣條件的狀態才叫做馬爾科夫狀態。即:
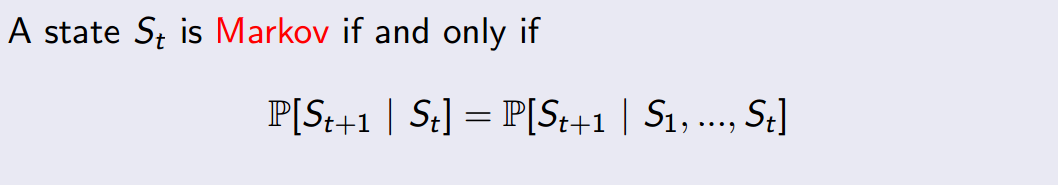
正是因為 State 太過於複雜,我們往往可以需要一個對 Environment 的觀察來間接獲得資訊,因此就有了 Observation。不過 Observation 是可以等於 State 的,在遊戲中,一幀遊戲畫面完全可以代表當前狀態,因此 Observation = State,此時叫做 Full Observability。
狀態、動作、狀態轉移概率組成了 MDP,一個 MDP 週期(episode )由一個有限的狀態、動作、獎勵佇列組成:
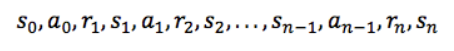
這裡 si 代表狀態,ai 代表行動,ri + 1(下標 i+1)是執行動作後的獎勵。 最終狀態為sn(例如“遊戲結束”)。
折扣未來獎勵(Discounted Future Reward)
為了獲得更多的獎勵,我們往往不能只看當前獎勵,更要看將來的獎勵。
給定一個 MDP 週期,總的獎勵顯然為:
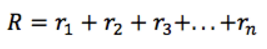
那麼,從當前時間 t 開始,總的將來的獎勵為:
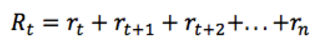
但是 Environment 往往是隨機的,執行特定的動作不一定得到特定的狀態,因此將來的獎勵所佔的權重要依次遞減,因此使用 discounted future reward 代替:
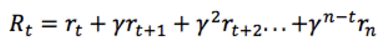
這裡 γ 是0和1之間的折扣因子 —— 越是未來的獎勵,折扣越多,權重越小。而明顯上式是個迭代過程,因此可以寫作:
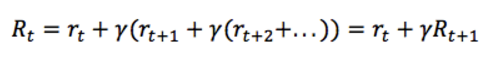
即當前時刻的獎勵等於當前時刻的即時獎勵加上下一時刻的獎勵乘上折扣因子 γ。如果 γ 等於0,意味著只看當前獎勵;如果 γ 等於1,意味著環境是確定的,相同的動作總會獲得相同的獎勵。因此實際中 γ 往往取類似0.9這樣的值。因此我們的任務變成了找到一個策略,最大化將來的獎勵 R。
Q-learning
在 Q-learning 中,我們定義一個函式 Q(s,a),表示在狀態 s 執行動作 a 時的最大折扣未來獎勵,並從此刻開始優化它:

把 Q(s,a) 看作是在狀態 s,執行動作 a時,遊戲結束時的分數就行了。不要驚奇為什麼在狀態 s 就可以知道遊戲結束時的分數,因為這是馬爾科夫過程,將來只和現在有關,現在是將來的充分條件。這樣最大化 Q(s,a) 就相當於最大化我們遊戲的得分了(至於為什麼叫做 Q,因為它代表了在特定狀態 s 下特定動作 a 的質量"quality")。
假設你處於狀態 s,思考應該採取行動 a 或 b 以在比賽結束時獲得最高分的動作。一旦有了 Q函式,答案就變得一目瞭然 —— 選擇 Q 值最高的動作:
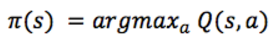
這裡的 π 代表策略,代表我們如何在某狀態選取動作。
怎麼才能得到這個Q函式呢? 只關注一個轉換 <s,a,r,s'>, 就像上一節中折扣未來獎勵一樣,我們可以用下一個狀態的Q值表示:
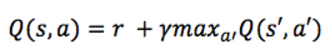
這就是貝爾曼方程(Bellman equation),當前狀態 s 的最大將來獎勵等於下一狀態 s' 的最大將來獎勵乘以折扣因子。這樣我們就可以用貝爾曼方程來近似了,最簡單的方法就是把Q函式看作二維陣列,行代表狀態,列代表動作,那麼演算法描述如下:

α是一個學習速率(learning rate),它控制了先前的Q值和新的Q值之間的差異有多少被考慮在內。 特別地,當α = 1時,則兩個 Q [s,a] 抵消,更新與貝爾曼方程完全相同。
我們用來更新 Q [s,a] 的 maxQ [s',a'] 一開始只是隨機的,但隨著迭代,會慢慢收斂,最終近似於真實值。具體的例子可以參看這裡:A Painless Q-Learning Tutorial (中文版:一個 Q-learning 演算法的簡明教程),詳細地一步一步介紹了是怎麼收斂的。

Deep Q Network
打磚塊遊戲中的環境狀態可以由擋板的位置,球的位置和方向以及每個磚塊的存在或不存在來定義。然而,這種直觀的表示只能代表具體的遊戲。有通用的方法適合所有的遊戲嗎?答案是螢幕畫素 —— 它們隱含地包含關於遊戲情況的所有相關資訊,球的速度和方向也可以包含在連續兩個螢幕畫素中。
如果我們使用 DeepMind 論文中的預處理方法,將遊戲畫面放縮為 84×84,並將其轉換為256灰度級的灰度級,我們將擁有 25684x84x4≈10的67970次方 個可能的遊戲狀態。這意味著Q表中有10的67970次方 行 —— 超過已知宇宙中的原子數!即使某些畫素組合永遠不會發生 —— 我們可以將其表示為僅包含訪問狀態的稀疏矩陣,但是,狀態還是很多,而且難以收斂。
這時候深度學習登場了,神經網路可以高效的表示高維資料,將其對映為低維資料。 因此我們可以用神經網路代表我們的Q函式,將狀態(遊戲畫面)和動作作為輸入,並輸出相應的Q值。 或者,我們只能將遊戲畫面作為輸入,並輸出每個可能動作的Q值。 這種方法的優點是,如果我們要執行Q值更新或選擇具有最高Q值的動作,我們只需要通過網路進行一次前進傳播,並且可以立即獲得所有動作的Q值 。
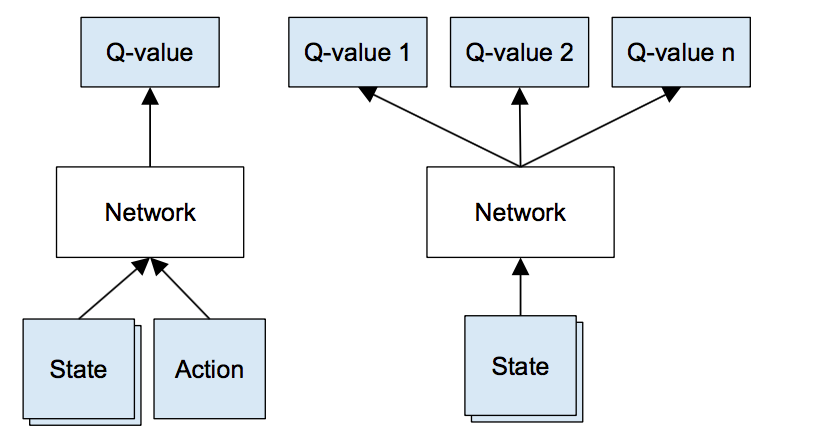
輸入是四個 84×84 灰度級遊戲畫面,輸出是每個可能動作的Q值(在Atari中為18)。 Q值可以是任何實際值,這使得它成為一個迴歸任務,可以用簡單的平方誤差損失進行優化:
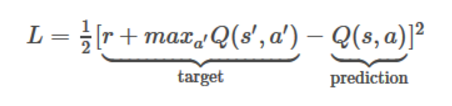
給定轉換 <s,a,r,s'>,Q表演算法需要修改為:
- 對當前狀態 s 進行前向傳播以獲取所有動作的Q值。
- 對下一個狀態 s' 進行前向傳播,並計算最大Q值 max Q(s’, a’)。
- 將動作對應的目標Q值設定為 r + γ max Q(s',a')(步驟2中計算的最大值)。
- 使用反向傳播演算法更新引數。
經驗回放 (Experience Replay)
現在我們使用卷積神經網路近似Q函式。但事實證明,使用非線性函式近似Q值不是非常穩定,而且難以收斂,在單GPU上需要很長時間,差不多一個星期才會看到成效。
有很多技巧可以優化,最重要的技巧是經驗回放。在遊戲過程中,所有的經歷 <s,a,r,s'> 儲存起來。訓練網路時,使用來自儲存的經驗,這打破了後續訓練樣本的相似性,而且可以平滑訓練結果。
探索與開發(Exploration-Exploitation)
首先,當Q表或Q網路被隨機初始化時,其預測最初也是隨機的。如果我們選擇具有最高Q值的動作,則該動作也將是隨機的,這時 Agent 執行的動作是隨機的。隨著Q函式的收斂,返回更一致的Q值,探索量將減少,此時這些一致的Q值叫做開發(Exploitation)。但是這些探索是“貪心”的,它發現第一個有效策略後停止收斂,很有可能我們只是找到了一個區域性最優解。
對於上述問題,一個簡單而有效的解決方案是 ε-greedy exploration —— 以概率 ε 選擇一個隨機動作,否則選擇具有最高Q值“貪婪”動作。DeepMind 實際上將 ε 隨時間從1減少到0.1,一 開始,系統完全隨機移動,最大限度地探索狀態空間,然後穩定的利用開發率。
最終帶有經驗回放的演算法如下:

DeepMind 還有更多的技巧來優化,如目標網路,錯誤剪輯,獎勵剪輯等,但這些都不在此介紹範圍之內。
實現
Q 演算法的 Q函式我麼可以用任何函式來代替,不限於神經網路或者卷積神經網路,因此我們需要把它抽象出來:
class Model():
def __init__(self, num_outputs):
self.num_outputs = num_outputs
def definition(self):
raise NotImplementedError
def get_num_outputs(self):
return self.num_outputsModel 代表了Q函式的抽象,num_outputs 代表了可能的動作個數,CartPole
中有兩個:左移或者右移;FlappyBird 也有兩個動作:點選螢幕或者什麼都不做。definition 函式代表具體的Q函式定義,返回輸入和輸出。
因為遊戲是不確定的,所以我們需要抽象一個 Env :
# Env-related abstractions
class Env():
def step(self, action_index):
raise NotImplementedError
def reset(self):
raise NotImplementedError
def render(self):
raise NotImplementedErrorEnv 可以是任何遊戲,或者其他問題。step 函式表示執行指定動作 action_index,然後返回一個元組:(state,
reward, terminal, info),state 是遊戲當前狀態,如螢幕畫素;reward 是獎勵,可以為負數; terminal 代表遊戲是否結束;info 代表一些其他資訊,可有可無。
然後是我們的演算法實現:
import numpy as np
import tensorflow as tf
import random
import numpy as np
import time
import sys
import collections
class DeepQNetwork():
def __init__(self,
model,
env,
optimizer=tf.train.AdamOptimizer,
learning_rate=0.001,
gamma=0.9,
replay_memeory_size=10000,
batch_size=32,
initial_epsilon=0.5,
final_epsilon=0.01,
decay_factor=1,
logdir=None,
save_per_step=1000,
test_per_epoch=100):
self.model = model
self.env = env
self.num_actions = model.get_num_outputs()
self.learning_rate = learning_rate
self.optimizer = optimizer
self.gamma = gamma
self.epsilon = initial_epsilon
self.initial_epsilon = initial_epsilon
self.final_epsilon = final_epsilon
self.decay_factor = decay_factor
self.logdir = logdir
self.test_per_epoch = test_per_epoch
self.replay_memeory = collections.deque()
self.replay_memeory_size = replay_memeory_size
self.batch_size = batch_size
self.define_q_network()
# session
self.sess = tf.InteractiveSession()
self.sess.run(tf.global_variables_initializer())
if self.logdir is not None:
if not self.logdir.endswith('/'): self.logdir += '/'
self.save_per_step = save_per_step
self.saver = tf.train.Saver()
checkpoint_state = tf.train.get_checkpoint_state(self.logdir)
if checkpoint_state and checkpoint_state.model_checkpoint_path:
path = checkpoint_state.model_checkpoint_path
self.saver.restore(self.sess, path)
print('Restore from {} successfully.'.format(path))
else:
print('No checkpoint.')
self.summaries = tf.summary.merge_all()
self.summary_writer = tf.summary.FileWriter(
self.logdir, self.sess.graph)
sys.stdout.flush()
def define_q_network(self):
self.input_states, self.q_values = self.model.definition()
self.input_actions = tf.placeholder(tf.float32,
[None, self.num_actions])
# placeholder of target q values
self.input_q_values = tf.placeholder(tf.float32, [None])
# only use selected q values
action_q_values = tf.reduce_sum(
tf.multiply(self.q_values, self.input_actions),
reduction_indices=1)
self.global_step = tf.Variable(0, trainable=False)
# define cost
self.cost = tf.reduce_mean(
tf.square(self.input_q_values - action_q_values))
self.optimizer = self.optimizer(self.learning_rate).minimize(
self.cost, global_step=self.global_step)
tf.summary.scalar('cost', self.cost)
tf.summary.scalar('reward', tf.reduce_mean(action_q_values))
def egreedy_action(self, state):
if random.random() <= self.epsilon:
action_index = random.randint(0, self.num_actions - 1)
else:
action_index = self.action(state)
if self.epsilon > self.final_epsilon:
self.epsilon *= self.decay_factor
return action_index
def action(self, state):
q_values = self.q_values.eval(feed_dict={self.input_states:
[state]})[0]
return np.argmax(q_values)
def do_train(self, epoch):
# randomly select a batch
mini_batches = random.sample(self.replay_memeory, self.batch_size)
state_batch = [batch[0] for batch in mini_batches]
action_batch = [batch[1] for batch in mini_batches]
reward_batch = [batch[2] for batch in mini_batches]
next_state_batch = [batch[3] for batch in mini_batches]
# target q values
target_q_values = self.q_values.eval(
feed_dict={self.input_states: next_state_batch})
input_q_values = []
for i in range(len(mini_batches)):
terminal = mini_batches[i][4]
if terminal:
input_q_values.append(reward_batch[i])
else:
# Discounted Future Reward
input_q_values.append(reward_batch[i] +
self.gamma * np.max(target_q_values[i]))
feed_dict = {
self.input_actions: action_batch,
self.input_states: state_batch,
self.input_q_values: input_q_values
}
self.optimizer.run(feed_dict=feed_dict)
step = self.global_step.eval()
if self.saver is not None and epoch > 0 and step % self.save_per_step == 0:
summary = self.sess.run(self.summaries, feed_dict=feed_dict)
self.summary_writer.add_summary(summary, step)
self.summary_writer.flush()
self.saver.save(self.sess, self.logdir + 'dqn', self.global_step)
# num_epoches: train epoches
def train(self, num_epoches):
for epoch in range(num_epoches):
epoch_rewards = 0
state = self.env.reset()
# 9999999999: max step per epoch
for step in range(9999999999):
# ε-greedy exploration
action_index = self.egreedy_action(state)
next_state, reward, terminal, info = self.env.step(
action_index)
# one-hot action
one_hot_action = np.zeros([self.num_actions])
one_hot_action[action_index] = 1
# store trans in replay_memeory
self.replay_memeory.append((state, one_hot_action, reward,
next_state, terminal))
# remove element if exceeds max size
if len(self.replay_memeory) > self.replay_memeory_size:
self.replay_memeory.popleft()
# now train the model
if len(self.replay_memeory) > self.batch_size:
self.do_train(epoch)
# state change to next state
state = next_state
epoch_rewards += reward
if terminal:
# Game over. One epoch ended.
break
# print("Epoch {} reward: {}, epsilon: {}".format(
# epoch, epoch_rewards, self.epsilon))
# sys.stdout.flush()
#evaluate model
if epoch > 0 and epoch % self.test_per_epoch == 0:
self.test(epoch, max_step_per_test=99999999)
def test(self, epoch, num_testes=10, max_step_per_test=300):
total_rewards = 0
print('Testing...')
sys.stdout.flush()
for _ in range(num_testes):
state = self.env.reset()
for step in range(max_step_per_test):
# self.env.render()
action = self.action(state)
state, reward, terminal, info = self.env.step(action)
total_rewards += reward
if terminal:
break
average_reward = total_rewards / num_testes
print("epoch {:5} average_reward: {}".format(epoch, average_reward))
sys.stdout.flush()解釋一下這個演算法:__init__ 方法除了 env 和 model 是必須的,其他都是可選的。
optimizer指定了 Tensorflow 使用的優化器;learning_rate是學習速率;gamma就是演算法中的折扣因子 γ;replay_memeory_size是存放經驗的最大數量;batch_size是從經驗池取經驗用於訓練的大小;epsilon就是 ε-greedy exploration 中的 ε,表示epsilon將從initial_epsilon以decay_factor的速率下降到final_epsilon為止,decay_factor等於1表示不下降;logdir是 Tensorflow 儲存模型的路徑,為None表示不儲存訓練結果;save_per_step是每多少步儲存一下斷點;test_per_epoch是每多少不測試評估一下訓練進度。
定義q network 的損失函式:
def define_q_network(self):
self.input_states, self.q_values = self.model.definition()
self.input_actions = tf.placeholder(tf.float32,
[None, self.num_actions])
# placeholder of target q values
self.input_q_values = tf.placeholder(tf.float32, [None])
# only use selected q values
action_q_values = tf.reduce_sum(
tf.multiply(self.q_values, self.input_actions),
reduction_indices=1)
self.global_step = tf.Variable(0, trainable=False)
# define cost
self.cost = tf.reduce_mean(
tf.square(self.input_q_values - action_q_values))
self.optimizer = self.optimizer(self.learning_rate).minimize(
self.cost, global_step=self.global_step)
tf.summary.scalar('cost', self.cost)
tf.summary.scalar('reward', tf.reduce_mean(action_q_values))然後是 train 方法:
# num_epoches: train epoches
def train(self, num_epoches):
for epoch in range(num_epoches):
epoch_rewards = 0
state = self.env.reset()
# 9999999999: max step per epoch
for step in range(9999999999):
# ε-greedy exploration
action_index = self.egreedy_action(state)
next_state, reward, terminal, info = self.env.step(
action_index)
# one-hot action
one_hot_action = np.zeros([self.num_actions])
one_hot_action[action_index] = 1
# store trans in replay_memeory
self.replay_memeory.append((state, one_hot_action, reward,
next_state, terminal))
# remove element if exceeds max size
if len(self.replay_memeory) > self.replay_memeory_size:
self.replay_memeory.popleft()
# now train the model
if len(self.replay_memeory) > self.batch_size:
self.do_train(epoch)
# state change to next state
state = next_state
epoch_rewards += reward
if terminal:
# Game over. One epoch ended.
break
# print("Epoch {} reward: {}, epsilon: {}".format(
# epoch, epoch_rewards, self.epsilon))
# sys.stdout.flush()
#evaluate model
if epoch > 0 and epoch % self.test_per_epoch == 0:
self.test(epoch, max_step_per_test=99999999)這裡我們把 (state,
one_hot_action, reward, next_state, terminal) 元組存在佇列中,如果佇列長度大於 batch_size 就開始訓練。
然後是具體的訓練:
def do_train(self, epoch):
# randomly select a batch
mini_batches = random.sample(self.replay_memeory, self.batch_size)
state_batch = [batch[0] for batch in mini_batches]
action_batch = [batch[1] for batch in mini_batches]
reward_batch = [batch[2] for batch in mini_batches]
next_state_batch = [batch[3] for batch in mini_batches]
# target q values
target_q_values = self.q_values.eval(
feed_dict={self.input_states: next_state_batch})
input_q_values = []
for i in range(len(mini_batches)):
terminal = mini_batches[i][4]
if terminal:
input_q_values.append(reward_batch[i])
else:
# Discounted Future Reward
input_q_values.append(reward_batch[i] +
self.gamma * np.max(target_q_values[i]))
feed_dict = {
self.input_actions: action_batch,
self.input_states: state_batch,
self.input_q_values: input_q_values
}
self.optimizer.run(feed_dict=feed_dict)
step = self.global_step.eval()
if self.saver is not None and epoch > 0 and step % self.save_per_step == 0:
summary = self.sess.run(self.summaries, feed_dict=feed_dict)
self.summary_writer.add_summary(summary, step)
self.summary_writer.flush()
self.saver.save(self.sess, self.logdir + 'dqn', self.global_step)首先隨機選擇一批資料,然後計算 Target Q 值,最後訓練即可。
接下來用真實的遊戲測試一下吧!
CartPole
CartPole 比較簡單,狀態只是一個一個4維的實數值向量,像這樣:
[-0.00042486 -0.02710707 0.01032103 -0.04882064]我們完全不用管這四個實數具體什麼意思,管它是什麼角度、加速度等,讓神經網路自己理解去吧!
定義我們的 CartPoleEnv,使用 Open AI 的 Gym:
class CartPoleEnv(Env):
def __init__(self):
self.env = gym.make('CartPole-v0')
def step(self, action_index):
s, r, t, i = self.env.step(action_index)
return s, r, t, i
def reset(self):
return self.env.reset()
def render(
相關推薦
Reinforcement Learning 的核心基礎概念及實現
2013 年倫敦的一家小公司 DeepMind 發表了一篇論文 Playing Atari with Deep Reinforcement Learning 。論文描述瞭如何教會電腦玩
Atari 2600 遊戲(僅僅讓電腦觀察遊戲的每一幀影象和接受遊戲分數的上升作為獎勵訊號)。結果很令人滿意,因為電腦比
第34課 棧的概念及實現(上)
操作符 cap ons 順序存儲 異常安全 city const text cte 1. 棧的概念
(1)棧是一種特殊的線性表
(2)棧僅能在線性表的一端進行操作
①棧頂(Top):允許操作的一端
②棧底(Bottom):不允許操作的一端
(3)棧的特性——後進先出
JavaScript中陣列相關基礎操作及實現
JavaScript中陣列操作比較靈活,關於js中陣列操作,寫了一些陣列操作程式碼,並在瀏覽器控制檯驗證。以下是js程式碼:
<script type="text/javascript">
console.log("---------------JavaScript陣列相關實
linux執行緒基礎概念及多執行緒程式設計
Linux中執行緒的概念:
首先,Linux中並不存在真在的執行緒。Linux中的執行緒是使用程序來模擬的。在一個程序需要同時執行多個執行流時,linux並不是開闢多個執行緒來執行,而是通過多個程序來模擬多個執行緒。
Linux中執行緒的實現原理:
首先先看一下張圖:
此時共有
佇列的基礎知識及實現方法
佇列
在網上又看到關於佇列的知識點,有很多,但都比較瑣碎,有的還有些錯誤,為方便自己理解,特整理出一篇,順便也加強記憶;當然,也附上我參考的部落格地址:
http://www.cnblogs.com/kaituorensheng/archive/2013/02/28/2
一、多執行緒基礎概念、實現執行緒三種方法、中斷執行緒方法,以及執行緒狀態轉化
1、CPU核心數和執行緒數的關係
1:1的關係,引入超執行緒之後,就是1:2
2、cpu時間輪轉機制,即RR排程
3、程序和執行緒
程序:程式執行資源分配最小單位,程序內部有多個執行緒,多個執行緒之間會共享程序資源
執行緒:CPU排程的最小單位
4、並行和併發
資料結構 筆記:佇列的概念及實現(上)
佇列是一種特殊的線性表
佇列僅能線上性表的兩端進行操作
-隊頭(Front):取出資料元素的一端
-隊尾(Rear):插入資料元素的一端
佇列的特性
-先進先出
佇列的操作
-建立佇列
-銷燬佇列(Queue())
-清空佇列(~Queue())
-進佇列
RocketMQ基礎概念及使用總結
一.瞭解RocketMQ?
rocketMQ是阿里開源的一款十分優秀的訊息佇列,rocketMQ具有很多其他訊息佇列不具有的特性,更重要的是rocketMQ是用java開發的學習成本較低,並且經歷了雙11的資料洪峰的考驗。rocketMQ已經加入了apache,成為apac
ELK & ElasticSearch 5.1 基礎概念及配置檔案詳解【轉】
轉自:https://blog.csdn.net/zxf_668899/article/details/54582849
1. 配置檔案
elasticsearch/elasticsearch.yml 主配置檔案
elasticsearch/jvm.options jvm引數配置檔案
Merkle Tree(默克爾樹或梅爾克爾樹)基礎概念及操作
Merkle Tree概念 Merkle Tree,通常也被稱作Hash Tree,顧名思義,就是儲存hash值的一棵樹。Merkle樹的葉子是資料塊(例如,檔案或者檔案的集合)的hash值。非葉節點是其對應子節點串聯字串的hash。[1] 1. Hash Hash
《SQL必知必會——第1、2課:sql基礎概念及檢索資料》
現在還會有這種想法,出於對技術的敬畏,在開始真正使用某項技術之前,都會翻翻相關書籍,潛心學習一下,然後在開始,所謂出生牛犢不怕虎,在軟體開發這個行業還是不提倡,一旦亂用技術,後面的坑實在難填。程式碼的改動就意味著除錯、測試,以及對生產環境的影響,是很花團隊時間和
分散式鎖概念及實現方式
分散式鎖概念
什麼是鎖?
在單程序的系統中,當存在多個執行緒可以同時改變某個變數(可變共享變數)時,就需要對變數或程式碼塊做同步,使其在修改這種變數時能夠線性執行,以防止併發修改變數帶來不可控的結果。
同步的本質是通過鎖來實現的。為了實現多個執行緒在一個時刻同一個程式碼塊只能有一個執行緒可執行,
python基礎概念及語法
程式設計基礎 現代計算機兩個著名的計算機任務一個是艾倫‘麥席森‘圖靈,被稱作計算機之父。提出著名的圖靈機為現代計算機的的邏輯工作方式奠定了基礎。另一人是馮諾依曼提出了二進位制,並且提出了計算機的五大部件。 就是馮諾依曼體系架構:輸入裝置、輸出裝置、儲存器、運算器
模型彙總18 強化學習(Reinforcement Learning)基礎介紹
1、背景介紹
學習和推理是人類智慧最重要的體現,為了使計算機也能夠像人一樣學習和決策,機器學習技術應運而生。機器學習利用計算機來模擬和實現人類學習和解決問題的過程,計算機系統通過不斷自我改進和學習,自動獲取知識並作出相應的決策、判斷或分析。機器學習是人工智慧的一個重要的
Netty(一):基礎概念及訊息處理流程
1. Netty是什麼?
Netty是由JBOSS提供的一個java開源網路通訊框架。Netty可以提供非同步的,非阻塞的,事件驅動的網路應用程式框架和工具,非常適合用來快速開發高效能、高可靠
c++記憶體模型------計算機系統核心概念及軟硬體實現
c++程式語言有3中不同類項的變數:全域性變數、區域性變數和動態分配變數。變數的值儲存在計算機的記憶體中,但是變數儲存的方式取決於變數的類項。3種類型的變數分別對應儲存器中3個特定的區域:
全域性變數存放在儲存器中的固定位置。區域性變數存放在執行時棧上。動態分配變數存放
Java併發核心基礎——執行緒池使用及底層實現機制詳解
Java執行緒池概述:
從使用入手:
java.util.concurrent.Executosr是執行緒池的靜態工廠,我們通常使用它方便地生產各種型別的執行緒池,主要的方法有三種:
1、newS
Elasticsearch基本概念及核心配置文件詳解
last log4j 強烈 內存 文檔 size oca 機制 集群 Elasticsearch5.X,下列的是Elasticsearch2.X系類配置,其實很多配置都是相互兼容的
1. 配置文件
config/elasticsearch.yml 主配置文件
【dubbo基礎】dubbo學習過程、使用經驗分享及實現原理簡單介紹
multi spring配置 不同 影響 為什麽 exception 同事 sock services 一、前言
部門去年年中開始各種改造,第一步是模塊服務化,這邊初選dubbo試用在一些非重要模塊上,慢慢引入到一些稍微重要的功能上,半年時間,學習過程及線上使用遇到的些問
Linux磁盤分區及文件系統管理之基礎概念
位圖 做的 訪問路徑 普通 磁盤分區 ffffff load 如何 區分 設備文件關聯至設備的驅動程序,是設備的訪問入口
設備號Major 主設備號,區分設備類型,用於標明設備所需要的驅動程序Minor 次設備號,區分同種類型下的不同設備
創建設備文件mknod 每一個設
