NP、NP-完全、NP-難問題
0. 基本定義
- 判定問題(decision problem):一個答案是
是或否的問題‘ - 無論是 P 問題,還是 NP 問題,NP-完全問題,NP-難問題,都是某類問題的總稱(集合),都是一種特定的 complexity classes;
1. 一張圖示
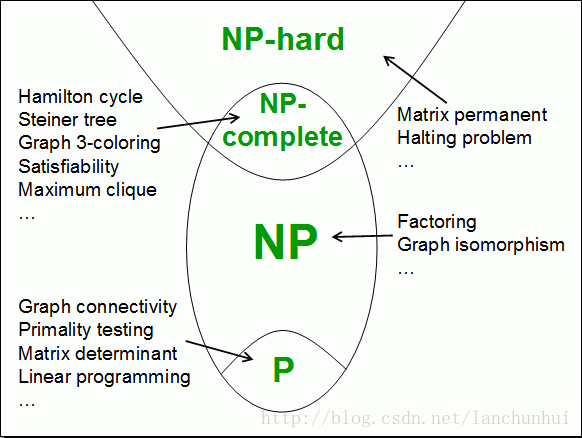
如圖示:
- P 問題是 NP 問題的子集;
- NP-完全是 NP 問題和 NP-難問題的交集;
相關推薦
NP、NP-完全、NP-難問題
0. 基本定義 判定問題(decision problem):一個答案是是或否的問題‘ 無論是 P 問題,還是 NP 問題,NP-完全問題,NP-難問題,都是某類問題的總稱(集合),都是一種特定
P問題、NP問題、NPC問題、NP難問題的概念
還是先用幾句話簡單說明一下時間複雜度。時間複雜度並不是表示一個程式解決問題需要花多少時間,而是當問題規模擴大後,程式需要的時間長度增長得有多快。也就是說,對於高速處理資料的計算機來說,處理某一個特定資料的效率不能衡量一個程式的好壞,而應該看當這個資料的規模變大到數百倍後,程式執行時間是否還是一樣,
p問題、np問題、npc問題、np難問題的理解(純屬個人見解)
最近因為要證明np問題,所以找了一系列概念去理解這4個問題。理解的時候看到好多人給出了不同的答案,我下面會借鑑別人的答案來總結出一份對於我自己來說,最容易理解這4個問題的說法。 預備知識瞭解: 時間複雜度 表明問題規模擴大後,程式需要的時間長度增長得有多快。程式的時
python中np.multiply()、np.dot()和星號(*)三種乘法運算的區別
圖片 分享 png blog details 分享圖片 blank net ref https://blog.csdn.net/zenghaitao0128/article/details/78715140 總結一下: python中np.multiply()、np.
P問題、NP問題、NPC問題、NP-hard問題詳解
要理解P問題、NP問題、NPC問題、NP-hard問題,需要先弄懂幾個概念: 什麼是多項式時間? 什麼是確定性演算法?什麼是非確定性演算法? 什麼是規約/約化? 多項式時間(Polynomial time) 什麼是時間複雜度? 時間複雜度並不是表示一個程式
np.dot()、np.multiply()、tf.matmul()、tf.multiply()
import tensorflow as tf import numpy as np x1 = ([[1, 2, 3], [1, 2, 3], [1, 2, 3]]) x2 = ([[2, 1, 1], [2, 1, 1], [2, 1, 1]]) y1 =
什麼是NP問題,什麼是NP hard問題,什麼是NP完全問題
假如老闆要你解決一個問題,你絞盡腦汁還是想不出來,叫天天不應,叫地地不靈,這時你走進老闆辦公室,可以採取3種策略: 1) 一副倒黴像,神情猥瑣,可憐巴巴的說:老闆,我沒做出來,我想我是太蠢了…… boss:蠢材!滾! (失敗……) 2) 雄赳赳氣昂昂跨進老闆辦公室,大吼一
java學習3創建學生屬性:學號、姓名、電話 完全實現對象集合的增刪改查。(控制臺來做)
main 使用 del ext str bre ack pri todo 首先創建一個student類其中包括get,set與構造函數 /** * */package work2; /** * @author Administrator * */public fina
01、完全、多重背包模板
int soft ont family color 限制 else 完全背包 log 背包問題: 背包總容量為W,有n件重量為weight[i],權值為value[i]的物品 1、01背包: 這是最基礎的背包問題,特點是:每種物品僅有一件,可以選擇放或不放。 1 void
MySQL完全、增量的備份與恢復
logs 文件夾 根據 輸入 local mes from vpd position 數據庫備份的重要性 提高系統的高可用性和災難可恢復性,在數據庫系統崩潰時,沒有數據備份就沒法找到數據。 使用數據庫備份還原數據庫,是數據庫崩潰時提供數據恢復最小代價的最優方案。 沒有數據
網站url路徑優化方法完全講解 (url優化、基於tp5、API接口開發)
dex 接下來 filename 配置文件 實現 tar 接口 官方 找到 url優化可是網站開發的必備高階技能,先看本實例優化前後效果比較: (同為調用前臺模塊下的index控制器下的index方法) 優化前:www.tp5.com/tp5/public/index.ph
命名空間的三種引用方式:非限定名稱、限定名稱、完全限定名稱
inf .cn const bsp domain spa 命名空間 turn 使用 1 //命名空間的三種引用方式:非限定名稱、限定名稱、完全限定名稱 2 3 namespace app\home; 4 const SET_NAME = ‘百度‘;
演算法導論 第十一章:散列表 筆記(直接定址表、散列表、通過連結法解決碰撞、雜湊函式、開放定址法、完全雜湊)
前面討論的各種資料結構中,記錄在各種結構中的相對位置是隨機的,和在記錄的關鍵字之間不存在有確定的關係,因此在查詢記錄是需要進行一系列和關鍵字的比較。而理想的情況是不希望進行任何的比較,一次存取便能得到所查記錄。那就必須在記錄的儲存位置和它的關鍵字之間建立一種確定的關係f,使每個關鍵字和結構中有一
藥代持證上崗、六不準、備案制,藥企營銷工作開展難!
“賽柏藍”微訊號報道顯示,三甲醫院發通知,藥代需持證上崗,浙江醫院已經給備案的藥代發“工作證”了,藥代進院需登記、領取並佩戴“工作證”,同時,醫院還給持證藥代定了六不準,交流業務需公開的規定,總而言之一句話,與銷售有關的事情,統統不能做。浙江省今年5月已陸續推行藥代備案制,也有資訊顯示,國家版本的備
安裝HBase--單節點、偽分散式、完全分散式安裝
1.下載HBase 連結:http://mirrors.cnnic.cn/apache/hbase/ 選擇 stable 目錄,下載 bin 檔案: 在Linux上解壓,部落格中解壓在/home/hadoop 目錄下: 進入解壓目錄: 2.修改配置 修改JD
史上最詳細、最完全的ipython使用教程,Python使用者必備!——ipython系列之二
宣告:本文承接前面一篇文章,ipython系列之一;另外,本文所指的ipython不是ipython notebook,ipython notebook已經被jupyter notebook所取代,不再叫ipython notebook了。 前面講解了ipython裡面的一些核心
史上最詳細、最完全的ipython使用教程,Python使用者必備!——ipython系列之一
一、ipython簡介 關於什麼是ipython,本文就不加以介紹了,他是一個非常流行的python直譯器,相比於原生的python直譯器,有太多優點和長處,因此幾乎是python開發人員的必知必會。 1、ipython相比於原生的python有什麼優勢 (1) pyth
np.random.rand()函式 與 np.random.randn()函式
一、np.random.rand() 本函式可以返回一個或一組服從“0~1”均勻分佈的隨機樣本值。隨機樣本取值範圍是[0,1),不包括1。 >>> import numpy as np >>> np.random.rand() 0.21844
資料庫篇——完全、增量備份和恢復
一、準備資料庫環境 1、搭建安裝環境 yum -y install \ gcc \ gcc-c++ \ make \ ncurses \ ncurses-devel \ bison \ Cmake 2、新增資料庫使用者useradd -s /sbin/nologin mysql //新增資料庫使用者3、
01揹包、完全揹包、多重揹包、分組揹包
參考連結: 各種揹包的描述: 01揹包(ZeroOnePack): 有N件物品和一個容量為V的揹包。(每種物品均只有一件)第i件物品的費用是c[i],價值是w[i]。求解將哪些物品裝入揹包可使價值總和最大。 完全揹包(CompletePack): 有N種
