機器學習技法第五週學習筆記
1.Soft-Margin SVM as Regularized Model
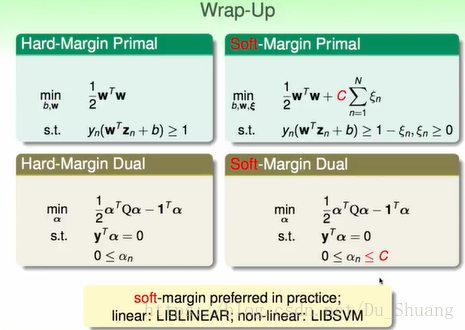
我們對hard-margin svm和soft-margin svm進行回顧,我們首先求出問題的基本式,然後轉換成對偶式,最後對對偶式利用二次規劃工具求解。
hard-margin svm的條件物理意義為希望資料能夠全部分對即Ein=0.最小化式子的物理意義為希望使求出邊界最大的分割線。
soft-margin svm的條件物理意義為希望資料能夠全部分對,但是能夠容忍一定的錯誤,並記錄錯誤的大小。最小化式子的物理意義為希望使求出邊界最大的分割線,但是同時錯誤最小。
最下面為推薦的兩個庫,是臺灣大學製作的SVM庫。
如果點離分割線的距離大於1即在邊界外,那麼此時沒有分錯ξ將會是等於0的,如果點離分割線的距離小於1但是大於0,那麼資料也不會被分錯,但是仍然會被扣分,此時ξ將不為0,如果點離分割線的距離小於0,那麼資料會被分錯,會被扣去較多的分。其中為點離分割線的距離。為點離線的最遠邊界的距離。
然後我們能夠將資料整合成一個式子,如下如所示。
這個式子和L2 regularization是類似的,可以寫成一個最小化式子和一個限制條件的和,並且求其最小值。
那麼我們為什麼不直接其進行求解呢?非要利用svm的解法求解呢?
很簡單,因為這不是個QP問題,不能使用核技巧,並且max運算子不能夠微分,所以很難求解。
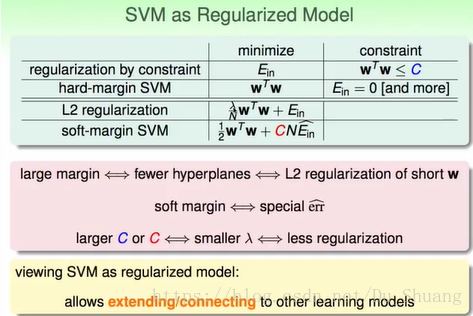
我們將正則化和svm的關聯進行總結。
一般的正則化:希望Ein最小,但是給一個限制條件,比如之前的正則化,我們希望Ein最小,但是我們通過條件限制了H的大小。
hard-margin SVM:我們希望所求邊界最寬,給定限制條件Ein必須等於0。
L2 regularization:希望所求邊界寬度和Ein的和最小,即Ein要小,w也要小。
soft-margin SVM: 在L2 regularization的基礎上增加了一個調節因子C。
這裡C相當於L1裡面的λ。大的C和小的λ相當於小的正則化。
既然我們不能夠用SVM的正則化形式求解,那麼我們為什麼要進行正則化呢?主要是因為這樣我們能夠用正則化形式將SVM與其他模型聯合起來進行分析比較。
2.SVM versus Logistic Regression
現在我們就通過SVM的正則化形式將其與我們之前的幾種分類演算法進行比較。
首先是01錯誤(最基本的錯誤):
然後是SVM的錯誤,當ys大於1時錯誤為0當小於1時錯誤成線型。
然後是邏輯迴歸的錯誤:
對比三種錯誤曲線,SVM和LRE都是01錯誤的上限,並且最大值和最小值都相等。所以這兩種錯誤相似。
三種錯誤的優缺點如下:
由上我們可知邏輯迴歸和svm的錯誤曲線是類似的,所以我們可以說邏輯迴歸是svm的近似,但是這個結論反過來正不正確呢?我們能不能用svm來對資料點為0或者1的概率進行預測呢?
3.SVM for Soft Binary Classification
這一節我們介紹怎麼才能利用SVM對資料是0或者1的概率進行估計。
一個直觀的想法是,我們直接對SVM求出的值帶入邏輯斯函式求得概率,實際上這個方法求得的值很接近真實的值,但是這樣我們失去了我們在邏輯迴歸中所推匯出來的一些結果。
另一個直觀的想法是我們利用svm求出的結果作為w0作為邏輯迴歸的遞推初始值。
但是這個方法並不比直接使用邏輯迴歸簡單,並且喪失了svm核函式的優勢。
為了中和兩種方法的優勢,於是有人提出了第三種想法:
首先利用svm求出一個分數,然後對這個分數進行一階邏輯迴歸。
通常的結果是A為正,B接近0,因為這樣也體現除了svm和邏輯迴歸的接近程度。
那麼這樣做的道理是什麼呢?
我們首先利用svm求得(b,w)這相當於將x轉換到了一個z空間。相當於利用了svm核函式的優勢。
然後對這個z空間的資料進行邏輯斯迴歸。
這樣我們就中和了這兩個方法的優勢。
這個結果和svm的結果相似。
4.Kernel Logistic Regression
上述我們是首先將資料通過svm轉換到z空間然後求解,這節我們將直接在z空間進行求解,而不需要svm的轉換。
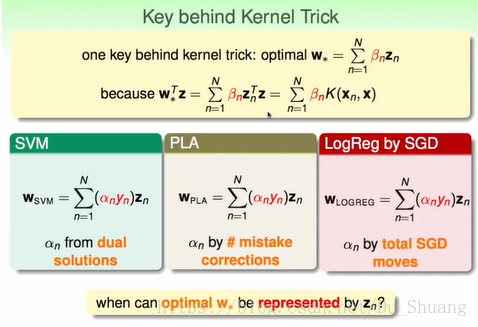
我們發現只要w能夠由z線型表示,那麼我們的結果用能使用核函式。而我們知道SVM,PLA和LogReg by SGD的w都是z的線型組合。
我們發現,只要w的求解滿足L2正則化形式,那麼我們的w就能被線型表示。
接下來我們用 kernel的方法來求解logistic Regression該方法稱為Kernel Logistic Regression.
我們直接將w表示成的線型組合,然後直接帶入原式利用帝都下降法求解。
上述模型的另一種解釋:不是很懂這個幻燈片的意義。