人工神經網路是模擬生物神經系統的。神經元之間是通過軸突、樹突互相連線的，神經元收到刺激時，神經脈衝在神經元之間傳播，同時反覆的脈衝刺激，使得神經元之間的聯絡加強。受此啟發，人工神經網路中神經元之間的聯絡(權值)也是通過反覆的資料資訊"刺激"而得到調整的。而反向傳播(back propagation)演算法就是用來調整權值的。

核心思想

訓練誤差逐層反向傳播，每層神經元與下層神經元間權重通過誤差最速梯度下降的方法調整。

演算法簡介

人工神經網路簡介

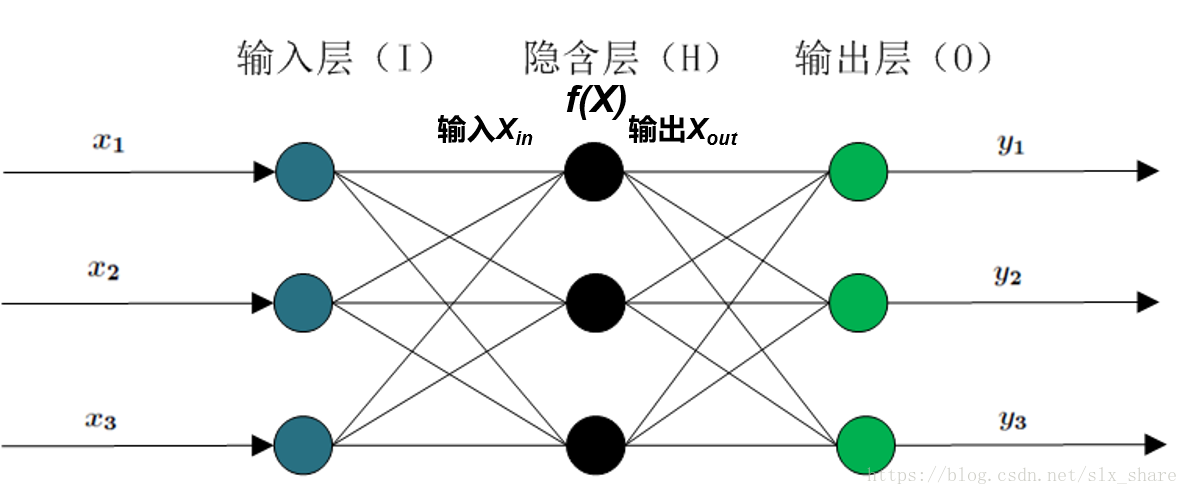
通常人工神經網路分為輸入層、隱藏層和輸出層。隱藏層和輸出層都有相應的激勵函式(模擬神經脈衝的激勵方式)。隱藏層可以為多層，但實際上不超過三層為好。如圖：

常用的激勵函式有sigmoid和linear函式。如果使用神經網路來做分類的工作，那麼輸出層激勵函式通常採用sigmoid, 若做迴歸工作，就採用linear函式。輸入層和輸出層神經元數目由訓練資料集而定，而隱藏層神經元數目的設定帶有很大的經驗性，對經驗公式$\sqrt {n_{input}+n_{output}} + 2$($n_{input},n_{output}$為輸入層、輸出層神經元數目)向上取整的數值可作為隱藏層神經元數目。

人工神經網路的前向傳播

訓練資料包含的資訊逐層從輸入層傳播到輸出層的方式是以感知機為基礎的。即$X_{}$

hidden_in=Winput_hiddenXinputXhidden_out=fhidden(Xhidden_in)Xoutput_in=Whidden_outputXhidden_outXoutput_out=foutput(Xoutput_in)X_{hidden\_in} = W_{input\_hidden}X_{input}\\X_{hidden\_out}=f_{hidden}(X_{hidden\_in})\\X_{output\_in} = W_{hidden\_output}X_{hidden\_out}\\X_{output\_out=f_{output}}(X_{output\_in})

誤差反向傳播

與前向傳播正好相反，訓練誤差都是從輸出層開始反向傳播到每個隱藏層。有了每一層的誤差就好辦了，訓練的目的就是減小誤差，即最小化期望風險，通常採用平方誤差損失函式$E = \frac{1}{2}(y_{pred}-y_{true})^2$，採用最速梯度下降法更新權值。
根據鏈式法則計算每層權值調整梯度:
--------------------------------------------------------------------------------------
舉例如下:

$\frac{\partial E}{\partial W_{input\_hidden}} = \frac{\partial E}{\partial X_{output\_out}}\frac{\partial X_{output\_out}}{\partial X_{output\_in}}\frac{\partial X_{output\_in}}{\partial X_{hidden\_out}}\frac{\partial X_{hidden\_out}}{\partial X_{hidden\_in}}\frac{\partial X_{hidden\_in}}{\partial W_{input\_hidden}}$ --------------------------------------------------------------------------------------

輸出層梯度：$\frac{\partial E}{\partial X_{output\_out}}=G_{out} = X_{output\_out}-y_{true}$即輸出層的誤差。

隱藏層到輸出層權值梯度：$G_{hidden\_out}=X_{hidden\_out}\delta_{hidden\_output}\\ \delta_{hidden\_output} = - G_{out} *f_{output}^{'}(X_{output\_in}) \\ 其中，\frac{\partial X_{output\_out}}{\partial X_{output\_in}} = f_{output}^{'}(X_{output\_in})$
輸入層到隱藏層權值梯度：$G_{input\_hidden}=X_{input}\delta_{input\_hidden}\\\delta_{input\_hidden} = \delta_{hidden\_output} W_{hidden\_output}*f_{hidden}^{'}(X_{hidden\_in}) \\ 其中，\frac{\partial X_{output\_in}}{\partial X_{hidden\_out}}=W_{hidden\_output},\frac{\partial X_{hidden\_out}}{\partial X_{hidden\_in}} = f_{hidden}^{'}(X_{hidden\_in})$

相關推薦