最小生成樹—Prim演算法和Kruskal演算法 (理解)
阿新 • • 發佈:2019-01-26
一個帶權連通無向圖中可能有多棵生成樹,所有生成樹中具有邊上的權值之和最小的樹稱為圖的最小生成樹。n個頂點的連通圖的生成樹有n個頂點、n-1條邊,性質如下:1.不能有迴路2.一個圖的最小生成樹不一定是唯一的,可能有多個。
1.在U中選擇一個頂點a加入V中。
2.向外(U-V)找到一個點b,使ab之間權值最小,把b也加入V中。
3.再以V中的點向外(U-V)尋找點使這個點與V權值最小並把點加入V中,以此類推,直到所有的頂點加入V中。 演算法分析: 1.任意一個頂點開始構造生成樹,將此頂點加入生成樹中,用一維陣列visit來標記哪些頂點已經加入了生成樹。
2.用dis陣列記錄生成樹到各個頂點的距離,(注意Dijkstra演算法記錄的才是源點到各個頂點的距離)初始化dis陣列。
3.從dis陣列中選出離生成樹最近(權值最小)的頂點(j)加入到生成樹中【即在陣列dis中找最小值】,再以j為中間點,更新生成樹到每個非樹頂點的距離(即鬆弛更新的過程),即如果dis[k]>e[j][k]則更新dis[k]=e[j][k]。
4.重複第三步,直到生成樹中有n個頂點為止。 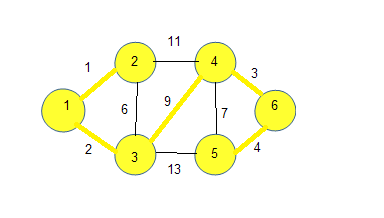
程式碼實現:
kruskal演算法——把森林合併為樹 演算法分析:把題目中所給的邊按照權值從小到大排序,每次從剩餘的邊中選取權值較小且邊的兩個頂點不在同一集合內的邊(就是不產生迴路的邊),加入到生成樹中,直到加入了n-1條邊。 程式碼實現:
測試樣例同上。
prim演算法——讓樹慢慢變大
圖G的頂點集合為U,生成樹的集合為V。1.在U中選擇一個頂點a加入V中。
2.向外(U-V)找到一個點b,使ab之間權值最小,把b也加入V中。
3.再以V中的點向外(U-V)尋找點使這個點與V權值最小並把點加入V中,以此類推,直到所有的頂點加入V中。 演算法分析: 1.任意一個頂點開始構造生成樹,將此頂點加入生成樹中,用一維陣列visit來標記哪些頂點已經加入了生成樹。
2.用dis陣列記錄生成樹到各個頂點的距離,(注意Dijkstra演算法記錄的才是源點到各個頂點的距離)初始化dis陣列。
3.從dis陣列中選出離生成樹最近(權值最小)的頂點(j)加入到生成樹中【即在陣列dis中找最小值】,再以j為中間點,更新生成樹到每個非樹頂點的距離(即鬆弛更新的過程),即如果dis[k]>e[j][k]則更新dis[k]=e[j][k]。
4.重複第三步,直到生成樹中有n個頂點為止。

程式碼實現:
#include<iostream> #include<cstring> using namespace std; int n,m,u,v,w; int e[111][111],dis[111],visit[111]; const int inf=9999999; //初始化 void init() { for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) { if(i==j) e[i][j]=0; else e[i][j]=inf; } } } //prim演算法 void prim() { int i,j,k,minn; //初始化dis陣列,這裡是1號點到各個頂點的初始距離,因為當前的生成樹中只有1號頂點。 for(i=1;i<=n;i++) { dis[i]=e[1][i]; } memset(visit,0,sizeof(visit)); //將一號頂點加入生成樹 visit[1]=1;//標記已加入。 int count=1,sum=0;//count記錄樹中的頂點的個數,sum記錄路徑之和。 while(count<n) { minn=inf; for(i=1;i<=n;i++) { if(visit[i]==0&&dis[i]<minn) { minn=dis[i]; j=i; } } visit[j]=1; count++; sum=sum+dis[j]; //掃描當前頂點j所有的邊,再以j為中間點,更新生成樹到每個非樹頂點的距離 for(k=1;k<=n;k++) { if(visit[k]==0&&dis[k]>e[j][k]) dis[k]=e[j][k]; } } cout<<sum<<endl; } int main() { int i,j,k; cin>>n>>m; //初始化 init(); //開始讀入邊 for(i=1;i<=m;i++) { cin>>u>>v>>w; //注意無向圖,所以需要將邊反向再儲存一遍 e[u][v]=w; e[v][u]=w; } //prim核心程式碼 prim(); return 0; }

kruskal演算法——把森林合併為樹 演算法分析:把題目中所給的邊按照權值從小到大排序,每次從剩餘的邊中選取權值較小且邊的兩個頂點不在同一集合內的邊(就是不產生迴路的邊),加入到生成樹中,直到加入了n-1條邊。 程式碼實現:
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> using namespace std; struct edge{ int u,v,w; }e[111]; int n,m; int pre[111]; //初始化 void init() { for(int i=1;i<=n;i++) { pre[i]=i; } } //並查集尋找祖先的函式 int find(int v) { if(pre[v]==v) return v; else { pre[v]=find(pre[v]); return pre[v]; } } //並查集的合併 int merge(int u,int v) { int t1=find(u); int t2=find(v); if(t1!=t2) { pre[t2]=t1; return 1; } return 0; } //對權值進行排序 bool cmp(edge a,edge b) { return a.w<b.w; } int main() { int i; cin>>n>>m; for(i=1;i<=m;i++) { cin>>e[i].u>>e[i].v>>e[i].w; } sort(e+1,e+m+1,cmp); //初始化 init(); //Kruskal演算法核心部分 int count=0,sum=0; for(i=1;i<=m;i++)//開始從小到大列舉每一條邊 { //判斷一條邊的兩個頂點是否已經連通 if(merge(e[i].u,e[i].v)) { count++; sum=sum+e[i].w; } if(count==n-1)//直到選用了n-1條邊之後退出迴圈。 break; } cout<<sum<<endl; return 0; }
測試樣例同上。
