[TOC]

0. 從零開始

 最近開始學習神經網路與機器學習，學校的暑期課程學習曲線比較陡，老師預設我們已經具備了很多基礎知識了，所以學起來很費力。所以就把自己的一些理解總結起來，放在這裡，供參考。

1. 啟用函式

1.1 sigmoid函式

• sigmoid函式是可微分的

  1.1.1 logistic函式

• 修改引數a可以改變曲線的傾斜程度
  -化成偽溫度T的形式後，T即用來控制噪聲水平的不確定性，當T趨於0時，該函式趨近閾值函式
  \[\phi(\nu) = \frac{1}{1 + \exp{(-a\nu)}} = \frac{1}{1 + \exp( \frac{-\nu}{T} )}\]

  1.1.2 雙曲正切函式
• 允許啟用函式取負值

• 值域為\((-1 , 1 )\)
  \[\phi(\nu) = tanh(\nu) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}\]

  1.1.3 閾值函式

• 比如最簡單的符號函式就是一種閾值啟用函式

• 不可微分
  \[ sgn(\nu)=\left\{ \begin{aligned} +1,\nu \geq 0 \\ -1,\nu < 0 \end{aligned} \right. \]

2. Rosenblatt感知器

 Rosenblatt感知器能夠對於線性可分的資料很好地分類，而其中機理與SVM、似然函式之類的方法不同。它包含了一個隱含的損失函式，同時也是可用用夾逼定理證明嚴格收斂的[2]。

2.1 Rosenblatt感知器虛擬碼

輸入：帶標籤的資料，其中輸入資料為m維，且共有N組資料，標籤\(l\)為閾值函式：
\[X = \{ x^i , l^i \} | i = 1,2,...N \}, x^i = (x_1^i, x_2^i,...,x_m^i), l^i \in \{+1, -1 \} \]
虛擬碼實現過程（參考1，不過做了一定的修改）：
for i = 1,2,...,N:
  \(\widehat{x}^i = (1 , x^i) = (1, x_1^i, x_2^i,..., x_m^i)\) // 對於內部偏置量的升維
  \(\widehat{x}^{'i} = \widehat{x}^{i}l^{i}\)

// 利用標籤label實現對於輸入資料的重新處理，方便後面直接採用
float w =< (m + 1) random float number >; // 隨機產生m+1維需要估計的引數
float \(\eta\) = ; // 學習率引數，通常取1，其實無所謂的，只是影響收斂速度
boollean errorDetect = true ;
while(errorDetected)
{
  errorDetected = false;
  for i = 1,2,...,N:
  if( $w^{T}\widehat{x}^{'i} < 0 $ ):
   errorDetected = true ;
   \(w = w + {\eta}\widehat{x}^{'i}\)
}
最終輸出：\(w\)

2.2 Rosenblatt感知器的視覺化向量理解

 考慮最簡單的一維資料的情況：

• 一維資料分佈在座標軸上：
  

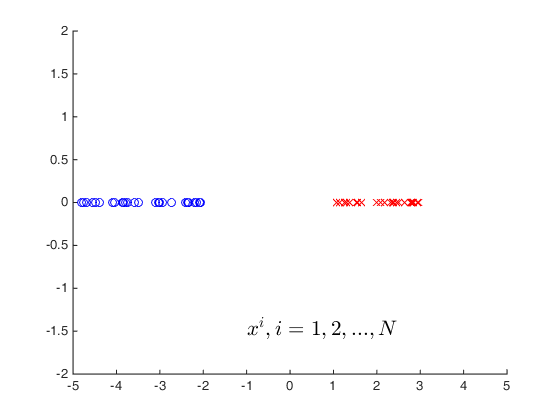
• 資料升維處理：
   此時，為了資料線性可分，權重向量\(w\)應當同圖中的紅色的點與原點構成的向量在90°以內，同藍色的點與原點構成的向量在90°以外；反之亦可，即保證，權重向量與可分資料向量的內積分別為正負。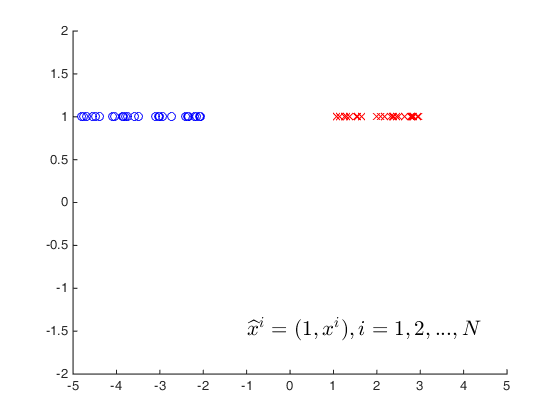
  

• 與標籤量相乘處理：
   這就等價於將藍色的向量繞原點旋轉180°，此時只需要權重向量與兩類向量的角度都在90°以內就滿足線性可分的要求了。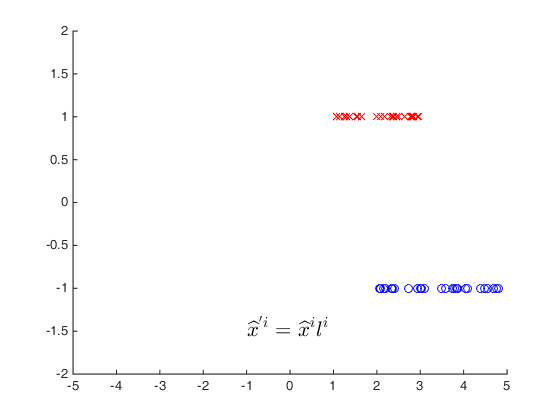
  

• 這裡說的比較簡單，只考慮了一維資料的情形，不過便於對於Rosenblatt工作原理的理解。

  2.3 Matlab程式碼：

clear;
clc ;
 
x1 = 1 + 2 * rand(25 , 1) ;
x2 = -2 - 3 * rand(30 , 1 ) ;
 
x11 = [ones(size(x1)) x1 ];
x22 = [- ones(size(x2)) -x2 ];
x = [x11 ; x22 ];
w = [0 ,0 ]; % 任意取的
 
errorDetected = 1 ; 
counter = 0 ;
while errorDetected == 1
        errorDetected = 0 ;
        for i = 1:size(x , 1)
            counter = counter + 1 ;
            if(w * x(i, :)' <= 0)
                errorDetected = 1 ;
                w = w + x(i, :) ;
            end
        end
end
        
w = w/norm(w); % 向量歸一化，便於顯示
temp = [w ;zeros(1 , 2 )];
 
figure(1)
scatter(x1 ,zeros(size(x1)) , 'xr');
hold on ;
plot(temp(: , 2) , temp(: , 1) , 'k' ); % 權重向量為黑線
scatter(x2 ,zeros(size(x2)) , 'ob');
set(gca , 'XLim' , [-5 5]);
set(gca , 'YLim' , [-2 2]);
 
text('Interpreter','latex','String','$$x^i, i = 1,2,...,N$$','Position',[-1 , -1.5],'FontSize',16);
hold off ;
 
figure(2)
scatter(x1 ,ones(size(x1)) , 'xr');
hold on ;
plot(temp(: , 2) , temp(: , 1) , 'k' ); % 權重向量為黑線
scatter(x2 ,ones(size(x2)) , 'ob');
set(gca , 'XLim' , [-5 5]);
set(gca , 'YLim' , [-2 2]);
text('Interpreter','latex','String','$$\widehat{x}^i =( 1, x^i), i = 1,2,...,N$$','Position',[-1 , -1.5],'FontSize',16);
hold off ;
 
figure(3)
scatter(x1 ,ones(size(x1)) , 'xr');
hold on ;
plot(temp(: , 2) , temp(: , 1) , 'k' ); % 權重向量為黑線
scatter(-x2 ,-ones(size(x2)) , 'ob');
set(gca , 'XLim' , [-5 5]);
set(gca , 'YLim' , [-2 2]);
text('Interpreter','latex','String','$$\widehat{x}^{''i} = \widehat{x}^{i}l^{i} $$','Position',[-1 , -1.5],'FontSize',16);
hold off ;

參考