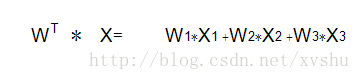本篇文章，我們開始介紹最簡單的神經網路結構，感知器，在瞭解原理的基礎上，下篇部落格我們程式碼實現一個單層感知器：

感知器：

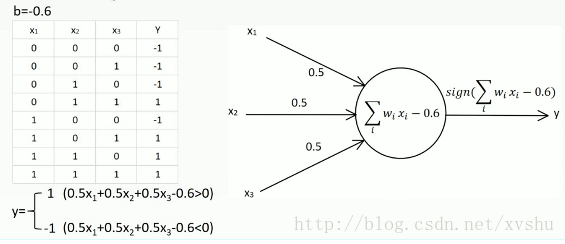
人工神經網路的第一個里程碑是感知機perceptron， 這個名字其實有點誤導， 因為它根本上是做決策的。 一個感知機其實是對神經元最基本概念的模擬 ，都未必有多少網路概念，他就是一個自動做決策的機器。比如說你要決定今天出不出去看電影， 你要考慮3個因素， 一個是女朋友在不在， 一個是電影好不好看， 另一個是今天有沒有工作， 這三個因素每個人的權重都不同，有的人看重女朋友， 有的人看重工作，所以權重就不等， 最後每個人根據自己的權重做出0或1，去或不去， to be or not to be的決策。那麼你怎麼做呢？ 你把三個要素按照它們需要的權重加和在一起， 在把這個分數送到一個叫sigmoid的門面前得到去或不去的決定， 工作原理如上圖。比單層感知機更復雜的多層感知機-或者我們常說的深度網路， 是進行資料處理和模式識別的利器。 深度神經網路之所以能夠處理這些資料型別，主要是因為這些資料本身具有的複雜結構很適合被NN識別， 而人類不需要預先設計識別這些結構的函式而是任由網路學習， D-CNN 深度卷積網路能夠同時看到一個影象從細節到抽象的結構，所以能夠抓住一些我們人類都說不出的細節。 

單層感知器：

 
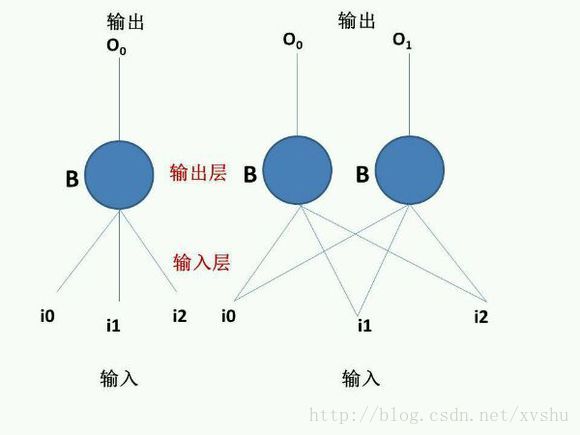
單層感知器可以用來區分線性可分的資料，並且一定可以在有限的迭代次數中收斂。 
從使用過程來看，單層的感知器其實看起來是相當簡單的：對假設函式進行訓練，直到對所有的樣本都滿足經過假設函式計算出來的結果與預期結果一致，就結束了。

單層感知器能夠用來模擬邏輯函式，例如邏輯非NOT、邏輯或非XOR、邏輯或OR、邏輯與AND和邏輯與非NAND等，但是不能用來模擬邏輯異或XOR（對於這個函式，必須用兩層神經元）。稍後將討論這個問題。 
除了輸入之外，偏置（bias）也經常被用於每個神經元，它在通過轉換函式之前被加到輸入的加權和上。權值也經常被應用於偏置上。偏置決定了多少輸入啟用（輸入的加權和）才能激發神經元進入興奮狀態。偏置往往被設定為1，而偏置的權值可以通過學習演算法加以調整。 
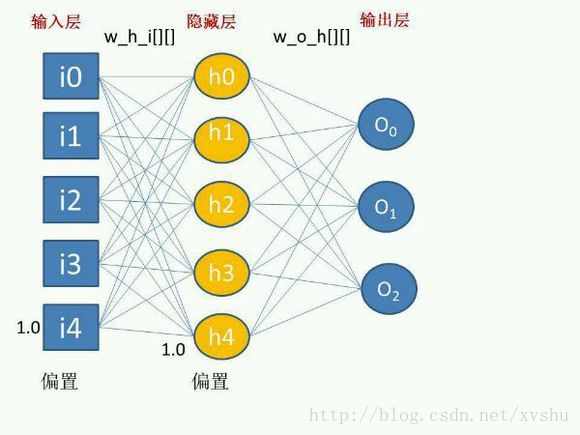
不應將單層感知器和單個神經元相混淆。如圖所示的網路就是一個單層感知器，因為它只由一層構成。對於多維問題，必須採用多層感知器。 
表示單層感知器非常簡單。由於輸入和權值存在一一對應關係，因此計算輸出是很容易的。

多層感知器：

Minsky和Papert在他們的Perception一書中揭示：單層感知器有一個缺點，即它們只能對線性可分的資料集進行分類。然而，此後不久人們就發現，如果見單層感知器疊加成多層感知器，則理論上就具備對任何分類問題的解決能力。事實上，多層感知器可以模擬成任意複雜的函式，其中函式的複雜性取決於網路輸入個數和隱層個數。 
多層感知器中神經元的性質和單層感知器中的一樣（例如偏置等）。然而由於存在多層，多層感知器中某一層的輸出就是下一層的輸入。因此多層感知器的實現比單層感知器略顯複雜，但還是很直觀的。注意，在這裡對隱層結點和輸出層結點使用相同的激勵函式，即sigmoid函式。Sigmoid函式可以將神經元的輸出值規格化到區間[0,1]。

該多層感知器有4個輸入單元，4個隱層單元和3個輸出單元。偏置作為輸入單元和隱層單元來處理，但偏置具有常數值1（雖然可以通過調整權值來改變偏置的影響）。 
程式的執行流程如下：首先，計算隱層單元的輸出（利用輸入單元和隱層單元到輸入層單元的權值）；然後，繼續計算下一層（這裡指輸出層）單元的輸出。通常這個過程被稱為前向傳送資料，或簡單的稱之為前饋（feed forward）。 
可以把神經網路看成平行計算系統。每個神經元是一個處理元件，該處理元件接受一個或多個輸入併產生一個輸出。輸入和輸出均可以看成資訊。在多層感知器架構中，輸出可以被送往多個其他處理單元，做進一步的處理。神經網路並行性的特性來自於同一層多個神經元之間的並行性。所有的神經元能夠同時處理它們各自的輸入，使得在多處理器系統中同一層次上具有大量神經元的神經網路的執行速度更快。

區別

相對於單層感知器，輸出端從一個變到了多個；輸入端和輸出端之間也不光只有一層，現在又兩層:輸出層和隱藏層。

數學模型

單層感知器由一個線性組合器和一個二值閾值元件組成。

輸入是一個N維向量 x=[x1,x2,…,xn]，其中每一個分量對應一個權值wi，隱含層輸出疊加為一個標量值：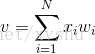 
　　　　　　　　　　　　　　　　　　　　 
隨後在二值閾值元件中對得到的v值進行判斷，產生二值輸出：

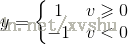
可以將資料分為兩類。實際應用中，還加入偏置，值恆為1，權值為b。這時，y輸出為：

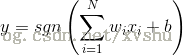
單層感知器結構圖：

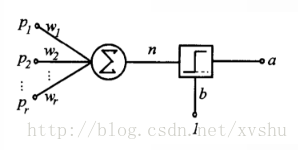
單層感知器進行模式識別的超平面由下式決定：

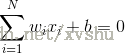
當維數N=2時，輸入向量可以表示為平面直角座標系中的一個點。此時分類超平面是一條直線:

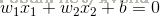
舉例：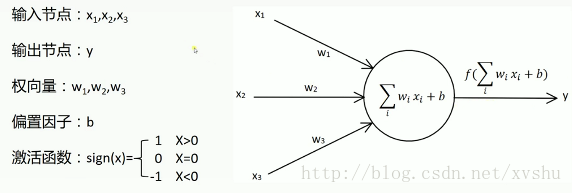 
　　　　　　　　　　 
下圖是個例子： 

偏置獨立作為輸入，為了統一公式：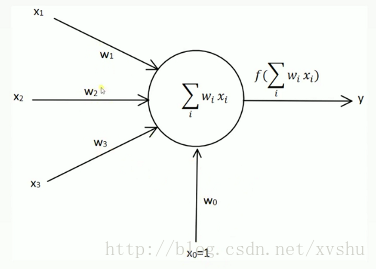 
　

權向量和輸入歸納為矩陣表達： 
　　 
 
　　　　 
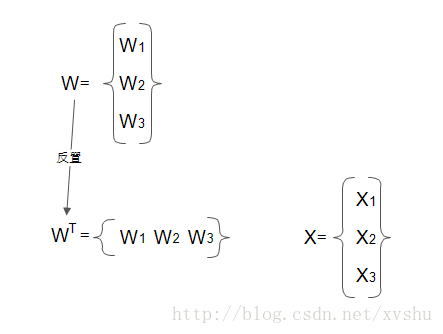
表示式更新為： 

匯出以下學習規則： 

總結： 
感知器的誕生意義就是有了一種自調節，收斂的識別演算法，雖然只是簡單的線性識別，但是在這個基礎之上改造就可以慢慢向更復雜，功能更全的識別邁進。