LeetCode中的動態規劃題目解答(3)
動態規劃是一種非常重要的演算法設計思想。歷史上有很多著名的演算法都是基於這種思想設計而來的,例如:Needleman–Wunsch演算法、CYK演算法、FFT演算法、維特比演算法等等。動態規劃的核心思想有兩個:首先是將一個大問題拆解為若干子問題;其次是將曾經計算過的結果儲存起來以備多次使用。
在本系列之前的文章中,我們已經介紹了動態規劃演算法設計的一種基本套路。但現實中的動態規劃問題其實是五花八門的。之前的動規例子的解答都使用了遞迴,本文所補充的兩個例子則採用迴圈。
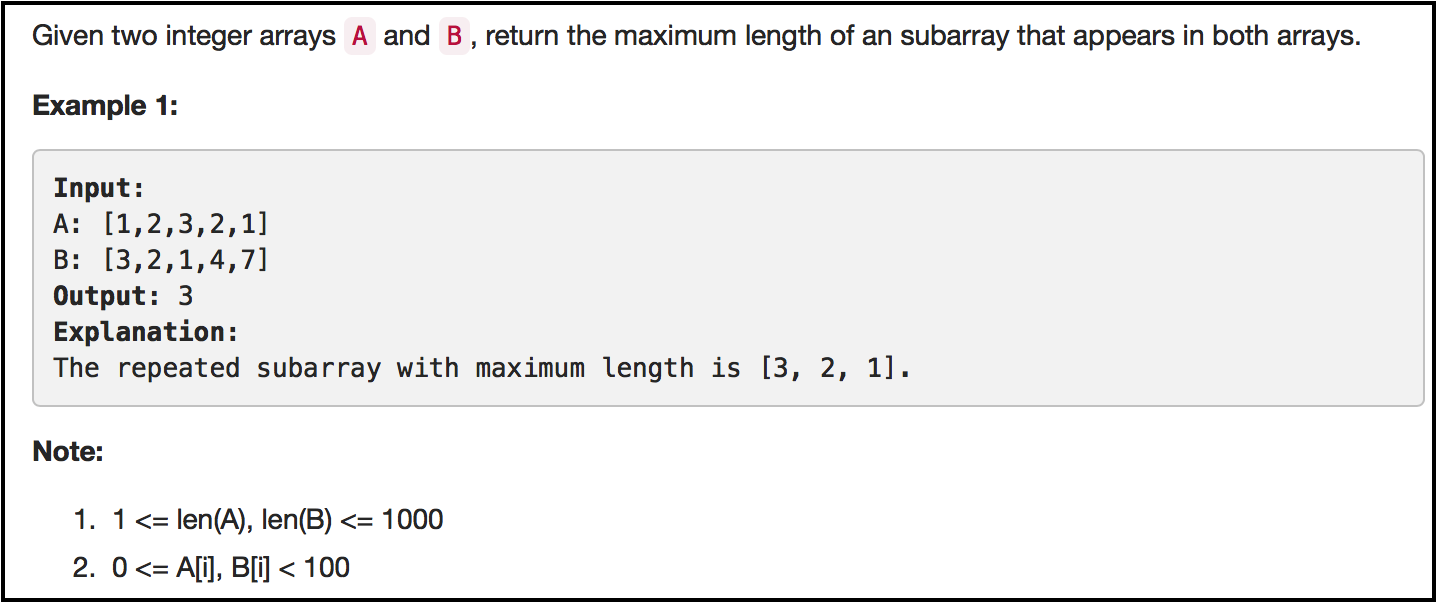
首先是LeetCode中的#718題(Maximum Length of Repeated Subarray)。該問題的描述如下:
動態規劃的一個核心思想是把之前已經得到的計算結果儲存起來,以備複用。這其實基本上就是在用空間換時間。就本題而言,為了儲存已經算過的結果,我們設計一個矩陣,並將其中的所有元素初始化為0。如果陣列A中的元素A[i]與陣列B中的元素B[j]相同,那麼就更新矩陣中的一個元素[i,j]為1+[i-1,j-1],1表示當前這個字元匹配,而[i-1,j-1]
class Solution { public: int findLength(vector<int>& A, vector<int>& B) { int m = A.size(); int n = B.size(); int ** matrix = new int*[m+1]; for(int i = 0; i < m+1; i++) { matrix[i] = new int[n+1]; for(int j = 0; j < n+1; j++) { matrix[i][j] = 0; } } int max = 0; for(int i = 1; i < m+1; i++) { for(int j = 1; j < n+1; j++) { if(A[i-1]==B[j-1]) { matrix[i][j] = 1 + matrix[i-1][j-1]; max = max > matrix[i][j] ? max : matrix[i][j]; } else matrix[i][j] = 0; } } return max; } };
上述程式碼可以滿足題目要求。另外注意到,上述實現中我們略去了“記憶體回收”的部分程式碼。當然,由於為了演示“動態規劃”的套路,這裡所採用的是一種非常樸素的實現方式、併為對其進行優化,你還可以改進它,以實現更高的效率。
與上面這道題目類似的還有#72題( Edit Distance)。該題目是要計算兩個單詞之間的編輯距離,其具體描述如下:
這道題目和前面的題目思路差不多,但是卻複雜很多。題目本身可以使用著名的德勒曼-溫施(Needleman-Wunsch)演算法直接解決。Needleman-Wunsch演算法也是歷史上最早的應用動態規劃思想設計的演算法之一。關於該演算法的更多內容,讀者可以參考《

需要說明的是,在具體使用Needleman-Wunsch
class Solution {
public:
int minDistance(string word1, string word2) {
int m = word1.size();
int n = word2.size();
if(m==0) return n;
if(n==0) return m;
int ** matrix = new int*[m+1];
int i = 0;
int j = 0;
int p = 0;
int q = 0;
for(i = 0; i < m+1; i++)
{
matrix[i] = new int[n+1];
matrix[i][0] = 0+i;
}
for(j = 0; j < n+1; j++)
{
matrix[0][j] = 0+j;
}
for(i = 1; i < m+1; i++)
{
for(j = 1; j < n+1; j++)
{
p = matrix[i][j-1] + 1 < matrix[i-1][j] + 1 ? matrix[i][j-1] + 1 : matrix[i-1][j] + 1;
if(word1[i-1]==word2[j-1])
{
q = matrix[i-1][j-1];
}
else
{
q = matrix[i-1][j-1] + 1;
}
matrix[i][j] = p < q ? p : q;
}
}
return matrix[m][n];
}
};(本文完)
本部落格中已經討論過的LeetCode題目列表