最小生成樹之克魯斯卡爾演算法 ( java版)
阿新 • • 發佈:2019-01-26
1 圖資料如下
二 Java程式碼
package leaning.graph; import java.util.ArrayList; import java.util.List; import leaning.graph.entity.Edge; /* * 克魯斯卡爾最小生成樹 * */ public class KruskalMiniCostSpanningTree { //計數器 private int counter = 0 ; private int[] parent = new int[9]; //邊集合 private List<Edge> edgesList = new ArrayList<Edge>(); //最大Int整數,表示無窮大 private int MAX_VALUE = Integer.MAX_VALUE; //定義節點 private String nodes[] = {"vo","v1","v2","v3","v4","v5","v6","v7","v8"}; //定義地圖變數 private int map[][] = new int[9][9]; public KruskalMiniCostSpanningTree(){ this.initMap(); this.initEdages(); } //初始化地圖 public void initMap(){ this.map[0] = new int[]{ 0, 10,MAX_VALUE,MAX_VALUE,MAX_VALUE, 11,MAX_VALUE,MAX_VALUE,MAX_VALUE}; this.map[1] = new int[]{ 10, 0, 18,MAX_VALUE,MAX_VALUE,MAX_VALUE, 16,MAX_VALUE, 12}; this.map[2] = new int[]{MAX_VALUE,MAX_VALUE, 0, 22,MAX_VALUE,MAX_VALUE,MAX_VALUE,MAX_VALUE, 8}; this.map[3] = new int[]{MAX_VALUE,MAX_VALUE, 22, 0, 20,MAX_VALUE,MAX_VALUE, 16, 21}; this.map[4] = new int[]{MAX_VALUE,MAX_VALUE,MAX_VALUE, 20, 0, 26,MAX_VALUE, 7,MAX_VALUE}; this.map[5] = new int[]{ 11,MAX_VALUE,MAX_VALUE,MAX_VALUE, 26, 0, 17,MAX_VALUE,MAX_VALUE}; this.map[6] = new int[]{MAX_VALUE, 16,MAX_VALUE,MAX_VALUE,MAX_VALUE, 17, 0, 19,MAX_VALUE}; this.map[7] = new int[]{MAX_VALUE,MAX_VALUE,MAX_VALUE, 16, 7,MAX_VALUE, 19, 0,MAX_VALUE}; this.map[8] = new int[]{MAX_VALUE, 12, 8, 21,MAX_VALUE,MAX_VALUE,MAX_VALUE,MAX_VALUE, 0}; } //初始化邊和權的list集合 public void initEdages(){ Edge v0 = new Edge(4,7,7); Edge v1 = new Edge(2,8,8); Edge v2 = new Edge(0,1,10); Edge v3 = new Edge(0,5,11); Edge v4 = new Edge(1,8,12); Edge v5 = new Edge(3,7,16); Edge v6 = new Edge(1,6,16); Edge v7 = new Edge(5,6,17); Edge v8 = new Edge(1,2,18); Edge v9 = new Edge(6,7,19); Edge v10 = new Edge(3,4,20); Edge v11 = new Edge(3,8,21); Edge v12 = new Edge(2,3,22); Edge v13 = new Edge(3,6,24); Edge v14 = new Edge(4,5,26); this.edgesList.add(v0); this.edgesList.add(v1); this.edgesList.add(v2); this.edgesList.add(v3); this.edgesList.add(v4); this.edgesList.add(v5); this.edgesList.add(v6); this.edgesList.add(v7); this.edgesList.add(v8); this.edgesList.add(v9); this.edgesList.add(v10); this.edgesList.add(v11); this.edgesList.add(v12); this.edgesList.add(v13); this.edgesList.add(v14); } //克魯斯卡爾演算法 public void kruskal(){ int n = - 1, m = -1 ,begin,end; for(int i=0 ; i < this.edgesList.size() ;i++){ //遍歷得到每一條邊 begin = this.edgesList.get(i).getBegin(); end = this.edgesList.get(i).getEnd(); n = this.find(begin); m = this.find(end); if(n!=m){ //說明沒有閉合線路 this.counter++; this.parent[n] = m; System.out.println(" 第 "+this.counter+" 條邊為 : ( "+this.nodes[this.edgesList.get(i).getBegin()]+" , "+this.nodes[this.edgesList.get(i).getEnd()]+" ) = "+this.edgesList.get(i).getWeight()+" "); } } } public int find(int index){ while(this.parent[index] > 0 ){ index = this.parent[index]; } return index; } public static void main(String[] args) { KruskalMiniCostSpanningTree kruskalMiniCostSpanningTree = new KruskalMiniCostSpanningTree(); kruskalMiniCostSpanningTree.kruskal(); } }
package leaning.graph.entity; /* * 克魯斯卡爾->最小生成樹邊實體 * */ public class Edge { private int begin; private int end; private int weight; public Edge(int begin, int end, int weight) { this.begin = begin; this.end = end; this.weight = weight; } public int getBegin() { return begin; } public void setBegin(int begin) { this.begin = begin; } public int getEnd() { return end; } public void setEnd(int end) { this.end = end; } public int getWeight() { return weight; } public void setWeight(int weight) { this.weight = weight; } }
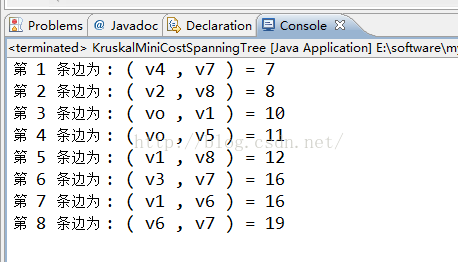
3 運算結果如下