本節主要是觀看Andrew Ng的斯坦福大學系列視訊CS299第6講、第7講等後，加上個人理解，對支援向量機部分做的一個筆記整理。
本文順序是：

• 綜述各個部分關係
• 最大間隔分類器
• 軟、硬間隔分類
• 核函式

2 最大間隔分類器

首先，我們應該知道求超平面與分類問題的正確性是與樣本點到超平面對的距離有直接關係的。吳恩達是用Logistic迴歸的例子來講述的這個問題：比如說θTx>>0時，我們可以非常自信的y=1（雖然還有很小的概率是y可能為0的）
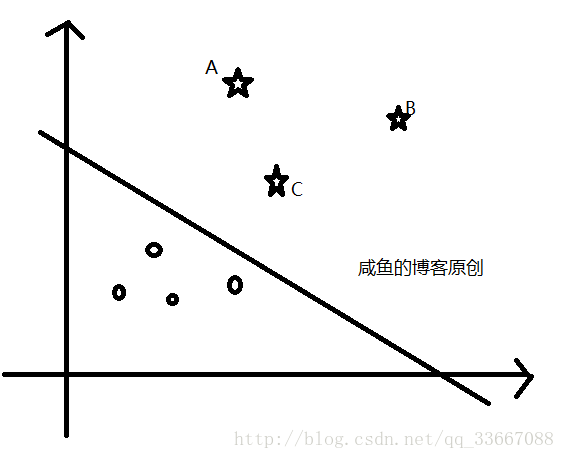
以此類推，以圖1為例。線將二維平面分成正反兩類，我們可以充分認為B屬於反類，而A也有很大可能屬於反類，但是C就不一定，它離分類超平面比較近。改變一點超平面的劃分，C可能到其他的分類。

基於這種情況，我們希望讓所有分類點都充分可以認為分類是正確的，需要它們都離分類超平面足夠遠。這個問題，我們可以在後文中用到幾何間隔來解決。
下面，來介紹下函式間隔和幾何間隔。
首先對圖一及後文所用函式做簡短介紹。

分類標籤y只能取-1或1，於圖一中，就是直線上方星星所在類標籤為1，圓點一方類標籤為-1（相反也可以）。
超平面分割線：

wTx+b
分類器為：hw,b(x)=g(wTx+b)當z>0時，g(z)=1;z<0,g(z)=−1
此處x與w的維度可以是多維。

？？這時我們分類器直接預測分類值，而不是像Logestic迴歸中預測y=1的可能性。

函式間隔：給定樣本點(x(i),y(i)),它的函式間隔受到（w,b）控制。它的函式間隔為

γ^(i)=y(i)(wTx+b)
對於整個訓練集S，我們可以定義整個訓練集的函式間隔為γ^=mini=1...mγ^(i)S=(x(i),y(i));i=1....m
一個非常大的正函式間隔使我們相信這個預測分類是置信區間足夠大的正確預測。
就是說如果y(i)(wTx+b)>>0，意味著分類正確（道理就是圖1中顯示道理，y僅僅是絕對值為1，影響預測正確性但不影響置信度）

但是這個定義存在一個問題，就是當（w,b）做等倍數變換的時候，超平面並沒有發生改變，但是函式間隔發生了改變。這顯然是不好的性質。因此，我們將w的大小固定，使函式間隔固定。將||w||=1時，這時的間隔就是幾何間隔。這裡給出幾何間隔定義：

γi=y(i)(wT||w||x+b||w||)γ=mini=1...mγ(i)S=(x(i),y(i));i=1....m
實際上，幾何間隔可以認為是歸一化後的函式間隔。幾何間隔就是點到超平面的距離（二維情況下是點到直線的距離）

現在我們來分析下基於上述概念得到的一些結論。二維的圖形見圖2。

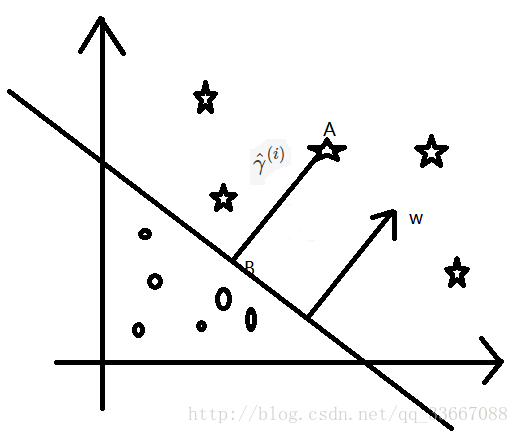
超平面的法向量是w(這個很好理解，多維情況下不明白可以參考解析幾何相關知識)。AB之間長度是幾何間隔γ(i)(假設幾何間隔大於0.超平面上側是y=1的分類),則B的位置是x(i)−γ(i)⋅w||w||.而顯然B在超平面上，因此有公式：

wT(x(i)−γ(i)w||w||)+b=0等式整

相關推薦

支援向量機（Support Vector machines）

本節主要是觀看Andrew Ng的斯坦福大學系列視訊CS299第6講、第7講等後，加上個人理解，對支援向量機部分做的一個筆記整理。 本文順序是： 綜述各個部分關係 最大間隔分類器 軟、硬間隔分類 核函式 2 最大間隔分類器 首先，我們應該知道求超

支援向量機（support vector machine）（一）：線性可分SVM

    總結一下，不然過段時間就全忘了，加油~     1、問題描述     假設，存在兩類資料A，B，如圖1所示，A中資料對應於圖中的實心點，B中資料對應圖中的空心點，現在我們需要得到一條直線，能夠將二者進行區分，這樣的線存在無數條，如圖1中的黑色直線所示，這些線都能夠

支援向量機（support vector machine）（二）：線性SVM

    通常情況下，存在以下兩種情況：    1、分類完全正確的超平面不一定是最好的；    2、樣本資料不是線性可分的；    如圖1所示，如果按照完全分對這個準則來劃分時，L1為最優分割超平面，但是實際情況如果按照L2來進行劃分，效果可能會更好，分類結果會更加魯棒。

淺談支援向量機（Support Vector Machine）

自從在學校安定下來後，小編的學習效率和時長提高了不少。在最近五天的時間裡，看了大約20節視訊並做了對應章節的程式設計練習。上一篇文章介紹了欠擬合和過擬合的知識，這次給小夥伴們介紹下支援向量機的知識。支援向量機和邏輯迴歸（Logistic Regression）很相像，從一方面

[完]機器學習實戰 第六章 支援向量機（Support Vector Machine）

[參考] 機器學習實戰（Machine Learning in Action） 本章內容 支援向量機（Support Vector Machine）是最好的現成的分類器，“現成”指的是分類器不加修改即可直接使用。基本形式的SVM分類器就可得到低錯

支援向量機（Support Vector Machine，SVM）——　線性SVM

  支援向量機（Support Vector Machine，簡稱 SVM）於 1995 年正式發表，由於其在文字分類任務中的卓越效能，很快就成為機器學習的主流技術。儘管現在 Deep Learning 很流行，SVM 仍然是一種很有的機器學習演算法，在資料集小的情況下能比 Deep Learning 取得更

【機器學習實戰-python3】支援向量機（Support Vecrtor Machines SVM）

工具：PythonCharm 書中的程式碼是python2的，而我用的python3，結合實踐過程，這裡會標註實踐時遇到的問題和針對python3的修改。 實踐程式碼和訓練測試資料可以參考這裡 https://github.com/stonycat/ML

【機器學習實戰】第6章 支援向量機（Support Vector Machine / SVM）

第6章 支援向量機 <script type="text/javascript" src="http://cdn.mathjax.org/mathjax/latest/MathJax.js?config=default"></script>

神經網路學習筆記-支援向量機（Support Vector Machine，SVM ）

基於誤差反向傳播演算法的多層感知器 徑向基函式網路 支援向量機（SupportVector Machine ， SVM ） 都是前饋神經網路 ，都用於解決模式分類與非線性對映問題 。 線性可分模

如何使用支援向量機（Support Vector Machine，SVM）思想解決迴歸問題

    迴歸問題的本質其實就是找到一根直線也好曲線也好，能夠最佳程度擬合我們的資料點，在這裡，怎樣定義擬合其實就是迴歸演算法的關鍵。比如說我們之前學過的線性迴歸演算法定義擬合的方式，就是讓我們的資料點到我們預測的直線相應的MSE的值最小，而對於SVM演算法的思路來說，對擬

機器學習之支援向量機： Support Vector Machines (SVM)

機器學習之支援向量機： Support Vector Machines (SVM) 歡迎訪問人工智慧研究網 課程中心 理解支援向量機（Understanding SVM） 使用支援向量機（Using SVM） 使用高斯核(Gaussian Kern

機器學習之支援向量機SVM Support Vector Machine (五) scikit-learn演算法庫

一、scikit-learn SVM演算法庫概述         scikit-learn中SVM的演算法庫分為兩類，一類是分類演算法庫，包括SVC、 NuSVC和LinearSVC三個類。另一類是迴歸演算法庫，包括SVR、NuSVR和LinearSVR三個類。相關的

機器學習總結（三）：SVM支援向量機（面試必考）

基本思想：試圖尋找一個超平面來對樣本分割，把樣本中的正例和反例用超平面分開，並儘可能的使正例和反例之間的間隔最大。 演算法推導過程： （1）代價函式：假設正類樣本y =wTx+ b>=+1,負

機器學習之支援向量機SVM Support Vector Machine (六) 高斯核調參

        在支援向量機（以下簡稱SVM）的核函式中，高斯核（以下簡稱RBF）是最常用的，理論上 RBF一定不比線性核函式差，但是在實際應用中，卻面臨幾個重要超引數的調優問題。如果調的不好，可能比線性核函式還要差。所以實際應用中，能用線性核函式得到較好效果的都會選擇

機器學習實戰（五）支援向量機SVM（Support Vector Machine）

目錄 0. 前言 1. 尋找最大間隔 2. 拉格朗日乘子法和KKT條件 3. 鬆弛變數 4. 帶鬆弛變數的拉格朗日乘子法和KKT條件 5. 序列最小優化SMO（Sequential Minimal Optimiz

機器學習與深度學習系列連載： 第一部分 機器學習（九）支援向量機2（Support Vector Machine）

另一種視角定義SVM：hinge Loss +kennel trick SVM 可以理解為就是hingle Loss和kernel 的組合 1. hinge Loss 還是讓我們回到二分類的問題，為了方便起見，我們y=1 看做是一類，y=-1 看做是另一類

機器學習——支援向量機SVM（Support Vector Machine）（下）

1、SVM演算法特徵 （1）訓練好的模型的演算法複雜度是由支援向量的個數決定的，而不是由資料的維度決定。所以，SVM不太容易產生overfitting。 （2）SVM訓練出來的模型完全依賴於支援向量（

Spark MLlib模型（一） 支持向量機【Support Vector Machine】

ssi p s ext edi sgd 訓練集 turn cati eight 目錄 　　支持向量機原理 　　支持向量機代碼(Spark Python) 支持向量機原理 　　待續... 返回目錄 支持向量機代碼(Spark Pytho

支援向量機（Python實現）

這篇文章是《機器學習實戰》（Machine Learning in Action）第六章 支援向量機演算法的Python實現程式碼。 1 參考連結 （1）支援向量機通俗導論(理解SVM的三層境界) （2）支援向量機—SMO論文詳解（序列最小最優化演算法） 2 實現程式

機器學習之支援向量機（四）

引言： 　　SVM是一種常見的分類器，在很長一段時間起到了統治地位。而目前來講SVM依然是一種非常好用的分類器，在處理少量資料的時候有非常出色的表現。SVM是一個非常常見的分類器，在真正瞭解他的原理之前我們多多少少都有接觸過他。本文將會詳細的介紹SVM的原理、目標以及計算過程和演算法步驟。我們針對線性可分資