支援向量機（support vector machine）（二）：線性SVM

阿新 • • 發佈：2018-12-09

通常情況下，存在以下兩種情況：

1、分類完全正確的超平面不一定是最好的；

2、樣本資料不是線性可分的；

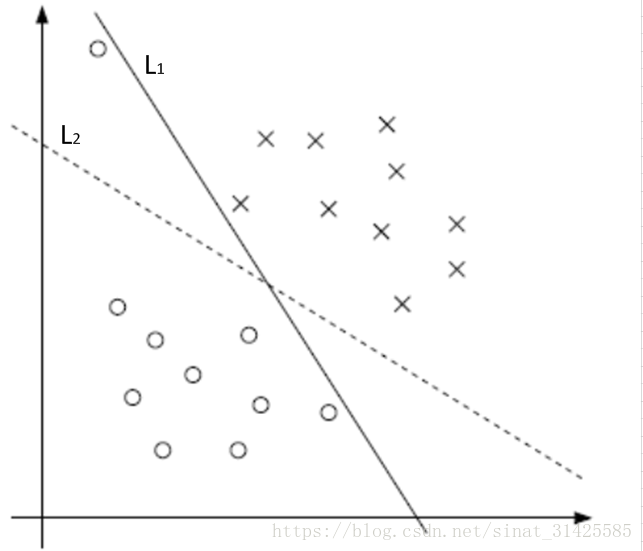
如圖1所示，如果按照完全分對這個準則來劃分時，L1為最優分割超平面，但是實際情況如果按照L2來進行劃分，效果可能會更好，分類結果會更加魯棒。

圖1 樣本分佈示意圖

通過引入鬆弛因子 $\xi _{i} >= 0$ ，放寬對於離群點的約束 $(\vec{W}^{T}\phi (\vec{X}_{i})+b)y_{i}>=1-\xi _{i}$ ，注意，如果 $\xi _{i}$ 任意大，任意超平面都會符合條件，因此我們需要對 $\xi _{i}$

做一定限制，目標函式就變成了：

$arg\ min_{\vec{W},b} \ \frac{1}{2} ||\vec{W}||+C\sum_{i=0}^{n}\xi _{i}$

$s.t. (\vec{W}^{T}\phi (\vec{X}_{i})+b)y_{i}\geqslant 1-\xi _{i},i=1,2,...,n$

$\xi _{i}\geqslant 0,i=1,2,...,n$

引入拉格朗日乘子有：

$L = \frac{1}{2} ||\vec{W}||^{2}+C\sum_{i=0}^{n}\xi _{i}-\sum_{i=1}^{n}\alpha _{i}((\vec{W}^{T}\phi (\vec{X}_{i})+b)y_{i}-1+\xi _{i} )-\sum_{i=1}^{n}\mu _{i}\xi _{i}$

將L分別對 $\vec{W},\xi,b$ 求偏導有：

$\vec{W}=\sum_{i=1}^{N}\alpha _{i}y_{i}\phi (\vec{x_{i}})$

$C-\alpha _{i}=\mu _{i},i=1,2,...,n$

$\sum_{i=1}^{N}\alpha _{i}y_{i}=0,i=1,2,...,n$

將三個條件回代到L有：

$L = \sum_{i=1}^{N}\alpha _{i}-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha _{i}\alpha _{j}\phi _( \vec {x_{i}})^{T}\phi _( \vec {x_{j}})$

約束條件為：

$s.t. \ \sum_{i=1}^{N}\alpha _{i}y_{i}=0,i=1,2,...,n$

$0\leqslant \alpha _{i} \leqslant C,i=1,2,...,n$

第二個約束條件是因為 $\mu _{i} \geqslant 0$ ，即 $C-\alpha _{i}\geqslant 0$ ，得 $\alpha _{i} \leqslant C$

這裡C需要預先設定引數，C越大，容許的 $\xi _{i}$ 就越小，對於離群點偏離群體的位置容忍度就越小，SVM對應排空區域（過渡帶）就越小，分類器容易發生過擬合；C越小，容許的 $\xi _{i}$ 就越大，對於離群點偏離群體的位置容忍度就越大，SVM對應排空區域（過渡帶）就越大，C如果過小，分類器的效能就會較差。

參考資料：

支援向量機通俗導論（理解SVM的三層境界）

周志華. 機器學習 : = Machine learning[M]. 清華大學出版社, 2016.

支援向量機（support vector machine）（二）：線性SVM

Spark MLlib模型（一）支持向量機【Support Vector Machine】

機器學習實戰（五）支援向量機SVM（Support Vector Machine）

支援向量機（support vector machine）（一）：線性可分SVM

支援向量機（support vector machine）（二）：線性SVM

機器學習與深度學習系列連載：第一部分機器學習（九）支援向量機2（Support Vector Machine）

支援向量機（Support Vector Machine，SVM）——　線性SVM

【機器學習實戰】第6章支援向量機（Support Vector Machine / SVM）

淺談支援向量機（Support Vector Machine）

機器學習——支援向量機SVM（Support Vector Machine）（下）

神經網路學習筆記-支援向量機（Support Vector Machine，SVM ）

如何使用支援向量機（Support Vector Machine，SVM）思想解決迴歸問題

[完]機器學習實戰第六章支援向量機（Support Vector Machine）

支援向量機演算法的實現和應用（Python3超詳細的原始碼實現+圖介紹）

支援向量機（Support Vector machines）

支援向量機--support vector machine

Andrew Ng 機器學習筆記 11 ：支援向量機(Support Vector Machine)

支援向量機(Support Vector Machine, SVM)

Support Vector Machine 支援向量機散點分類

支援向量機的公式推導(Support Vector Machine，SVM)

周志華《Machine Learning》學習筆記（7）--支援向量機

支援向量機（support vector machine）（二）：線性SVM

相關推薦