影象的骨架似乎沒有嚴格的數學定義，可認為是影象細化（Thinning）的產物（中軸可以看作一種骨架，其有嚴格的數學定義）。目前已經有許多細化演算法，這些演算法得到的骨架可能略有差異。本文實現了Khalid Sheed 的 K3M演算法。該演算法屬於迭代腐蝕邊界的一類演算法，該類演算法的思想是，假定從二值影象中物體的邊界處同時開始燃燒，物體就會被逐步細化，但在燃燒過程中要保證滿足一定條件的點被保留或者被“燒掉”，以確定燃燒結束後，剩下的最後一畫素寬的影象為影象的骨架。這些條件的確定沒有統一的標準，各個演算法採取了不同的方案。一般來講，為了滿足計算的速度要求和演算法的準確，迭代中演算法會對影象邊界上某點的3*3鄰域內進行檢查，判斷是否滿足要求。

K3M演算法在每次迭代中需要進行六次檢查

Phase 0. 標記出影象的邊界，

Phase 1. 如果該點的鄰域中有3個點（非零，以下皆如此）相鄰，刪除該點

Phase 2. 如果該點的鄰域中有3或4個點相鄰，刪除該點。

Phase 3. 如果該點的鄰域中有3，4，5個點相鄰，刪除該點。

Phase 4. 如果該點的鄰域中有3，4，5，6個點相鄰，刪除該點。

Phase 5. 如果該點的鄰域中有3，4，5，6，7個點相鄰，刪除該點。

Phase 6. 剩餘的邊界點取消標記，如果Phase 5中沒有點被修改，停止迭代，否則返回Phase 0。

具體的步驟可以閱讀論文：http://matwbn.icm.edu.pl/ksiazki/amc/amc20/amc2029.pdf

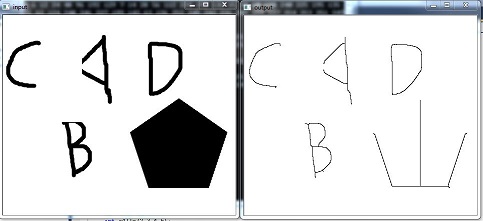
演算法的測試結果如下：

參考：

#include <opencv2/imgproc/imgproc.hpp>
#include <opencv2/objdetect/objdetect.hpp>
#include <opencv2/highgui/highgui.hpp>
#include<vector>
#include<iostream>
#include<algorithm>

using std::vector;

vector<int> GetFlags(int a[],int length)
{
	vector<int> vec;
	int neighbour[]={1,2,4,8,16,32,64,128,1,2,4,8,16,32,64};
	for(int i=0;i<length;i++)
	{
		for(int j=0;j<8;j++)
		{
			int sum=0;
			for(int k=j;k<=j+a[i];k++)
				sum+=neighbour[k];
			vec.push_back(sum);
			std::cout<<sum<<" ";
		}
	}
	std::cout<<std::endl;
	return vec;
}
void skeleton(cv::Mat &Input) //Input-binary image
{
	int a0[]={1,2,3,4,5,6};
	int a1[]={2};
	int a2[]={2,3};
	int a3[]={2,3,4};
	int a4[]={2,3,4,5};
	int a5[]={2,3,4,5,6};
	vector<int> A0=GetFlags(a0,6);

	vector<int> A1=GetFlags(a1,1);

	vector<int> A2=GetFlags(a2,2);
	vector<int> A3=GetFlags(a3,3);
	vector<int> A4=GetFlags(a4,4);
	vector<int> A5=GetFlags(a5,5);
	vector<cv::Point2i> border;
	bool modify=true;
	int neighbour[3][3]={
		{128,1,2},
		{64,0,4},
		{32,16,8}
	};
	int row=Input.rows;
	int col=Input.cols;
	while(modify)
	{
		modify=false;
		// flag the border Pharse 0
		for(int m=1;m<row-1;++m)
		{
			for(int n=1;n<col-1;++n)
			{
				int weight=0;
				for(int j=-1;j<=1;++j)
				{
					for(int k=-1;k<=1;k++)
					{
						weight+=neighbour[j+1][k+1]*Input.at<uchar>(m+j,n+k);
					}
				}
				if(std::find(A0.begin(),A0.end(),weight)!=A0.end())
					border.push_back(cv::Point2i(m,n));
			}
		}
		//Pharse 1
		vector<cv::Point2i>::iterator first=border.begin();
		while(first!=border.end())
		{
			int weight=0;
			for(int j=-1;j<=1;++j)
			{
				for(int k=-1;k<=1;k++)
				{
					weight+=neighbour[j+1][k+1]*Input.at<uchar>((*first).x+j,(*first).y+k);
				}
			}
			if(std::find(A1.begin(),A1.end(),weight)!=A1.end())
			{
				Input.at<uchar>((*first).x,(*first).y)=0;
				first=border.erase(first);
			}
			else
			++first;
		}
		//Pharse2
		first=border.begin();
		while(first!=border.end())
		{
			int weight=0;
			for(int j=-1;j<=1;++j)
			{
				for(int k=-1;k<=1;k++)
				{
					weight+=neighbour[j+1][k+1]*Input.at<uchar>((*first).x+j,(*first).y+k);
				}
			}
			if(std::find(A2.begin(),A2.end(),weight)!=A2.end())
			{
				Input.at<uchar>((*first).x,(*first).y)=0;
				first=border.erase(first);
			}
			else
			++first;
		}
		//Pharse3
		first=border.begin();
		while(first!=border.end())
		{
			int weight=0;
			for(int j=-1;j<=1;++j)
			{
				for(int k=-1;k<=1;k++)
				{
					weight+=neighbour[j+1][k+1]*Input.at<uchar>((*first).x+j,(*first).y+k);
				}
			}
			if(std::find(A3.begin(),A3.end(),weight)!=A3.end())
			{
				Input.at<uchar>((*first).x,(*first).y)=0;
				first=border.erase(first);
			}
			else
			++first;
		}
		//Pharse4
		first=border.begin();
		while(first!=border.end())
		{
			int weight=0;
			for(int j=-1;j<=1;++j)
			{
				for(int k=-1;k<=1;k++)
				{
					weight+=neighbour[j+1][k+1]*Input.at<uchar>((*first).x+j,(*first).y+k);
				}
			}
			if(std::find(A4.begin(),A4.end(),weight)!=A4.end())
			{
				Input.at<uchar>((*first).x,(*first).y)=0;
				first=border.erase(first);
			}
			else
			++first;
		}
		//Pharse5
		first=border.begin();
		while(first!=border.end())
		{
			int weight=0;
			for(int j=-1;j<=1;++j)
			{
				for(int k=-1;k<=1;k++)
				{
					weight+=neighbour[j+1][k+1]*Input.at<uchar>((*first).x+j,(*first).y+k);
				}
			}
			if(std::find(A5.begin(),A5.end(),weight)!=A5.end())
			{
				Input.at<uchar>((*first).x,(*first).y)=0;
				first=border.erase(first);
				modify=true;
			}
			else
			++first;
		}
		//Pharse6
		border.clear();
	}
	for(int m=1;m<row-1;++m)
	{
		for(int n=1;n<col-1;++n)
		{
			int weight=0;
			for(int j=-1;j<=1;++j)
			{
				for(int k=-1;k<=1;k++)
				{
					weight+=neighbour[j+1][k+1]*Input.at<uchar>(m+j,n+k);
				}
			}
			if(std::find(A0.begin(),A0.end(),weight)!=A0.end())
					Input.at<uchar>(m,n)=0;;
		}
	}

}
int main()
{
	cv::Mat raw=cv::imread("test.bmp");
	cv::Mat image(raw.rows,raw.cols,CV_8UC1);
	cv::cvtColor(raw,image,CV_RGB2GRAY);
	cv::Mat binaryImage(image.rows,image.cols,CV_8UC1);
	cv::threshold(image,binaryImage,150,1,CV_THRESH_BINARY_INV);

	cv::imshow("input",image);
	skeleton(binaryImage);
		for(int p=0;p<binaryImage.rows;p++)
		{
			for(int q=0;q<binaryImage.cols;q++)
			{
				if(binaryImage.at<uchar>(p,q)==1)
					binaryImage.at<uchar>(p,q)=0;
				else
					binaryImage.at<uchar>(p,q)=255;
			}
		}
	cv::imshow("output",binaryImage);

	cv::waitKey(0);
	return 0;
}