移動平均法(Moving average,MA) 指數平滑法(Exponential Smoothing,ES)
____tz_zs
注:本部落格中關於概念的解釋部分均來自 MBA智庫百科
一、移動平均法(Moving average,MA)
移動平均法又稱滑動平均法、滑動平均模型法
移動平均法是用一組最近的實際資料值來預測未來一期或幾期內公司產品的需求量、公司產能等的一種常用方法。移動平均法適用於即期預測。當產品需求既不快速增長也不快速下降,且不存在季節性因素時,移動平均法能有效地消除預測中的隨機波動,是非常有用的。移動平均法根據預測時使用的各元素的權重不同,可以分為:簡單移動平均和加權移動平均。
移動平均法是一種簡單平滑預測技術,它的基本思想是:根據時間序列資料、逐項推移,依次計算包含一定項數的序時平均值,以反映長期趨勢的方法。因此,當時間序列的數值由於受週期變動和隨機波動的影響,起伏較大,不易顯示出事件的發展趨勢時,使用移動平均法可以消除這些因素的影響,顯示出事件的發展方向與趨勢(即趨勢線),然後依趨勢線分析預測序列的長期趨勢。
(一)簡單移動平均法
簡單移動平均的各元素的權重都相等。簡單的移動平均的計算公式如下:
Ft=(At-1+At-2+At-3+…+At-n)/n
式中,
Ft--對下一期的預測值;
n--移動平均的時期個數;
At-1--前期實際值;
At-2,At-3和At-n分別表示前兩期、前三期直至前n期的實際值。
小Demo
.
import matplotlib.pyplot as plt # 簡單移動平均法 def ma(list2): n = len(list2) sum = 0 for i in list2: sum += i result = sum / n return result def answer1(list1, n): # 簡單移動平均法 listMA = [] # 簡單移動平均值的列表 for i in range(n - 1, len(list1)): # print(i) list2 = (list1[i - (n - 1):i + 1]) listMA.append(ma(list2)) print("簡單移動平均值的列表:{}".format(listMA)) # 最後的移動平均值可做為下一個數的預測 x = listMA[-1] print("下一個數的預測:{}".format(x)) # 畫圖 plt.scatter(list(range(len(listMA))), listMA) plt.show() if __name__ == '__main__': list1 = [1, 2, 4, 5, 6, 8, 10, 12, 14, 16, 19, 24, 29] # 13個 n = 3 # 移動平均期數 answer1(list1, n) # 簡單移動平均法
.
執行結果:
.
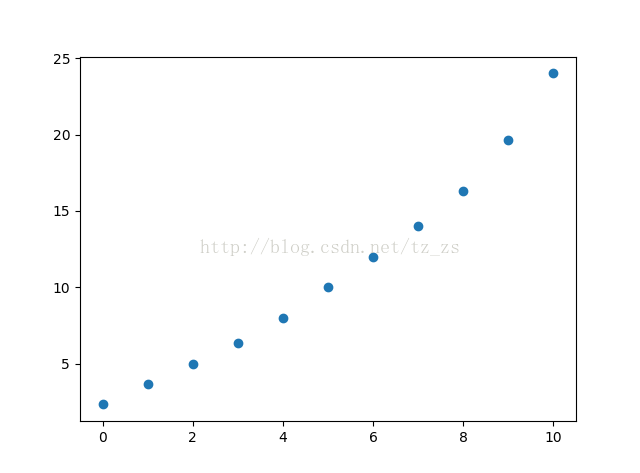
簡單移動平均值的列表:[2.3333333333333335, 3.6666666666666665, 5.0, 6.333333333333333, 8.0, 10.0, 12.0, 14.0, 16.333333333333332, 19.666666666666668, 24.0]
下一個數的預測:24.0.
簡單移動平均值散點圖:
(二)加權移動平均法
加權移動平均給固定跨越期限內的每個變數值以不同的權重。其原理是:歷史各期產品需求的資料資訊對預測未來期內的需求量的作用是不一樣的。除了以n為週期的週期性變化外,遠離目標期的變數值的影響力相對較低,故應給予較低的權重。 加權移動平均法的計算公式如下:
Ft=w1At-1+w2At-2+w3At-3+…+wnAt-n
式中,
w1--第t-1期實際銷售額的權重;
w2--第t-2期實際銷售額的權重;
wn--第t-n期實際銷售額的權重;
n--預測的時期數;w1+ w2+…+ wn=1
在運用加權平均法時,權重的選擇是一個應該注意的問題。經驗法和試演算法是選擇權重的最簡單的方法。一般而言,最近期的資料最能預示未來的情況,因而權重應大些。例如,根據前一個月的利潤和生產能力比起根據前幾個月能更好的估測下個月的利潤和生產能力。但是,如果資料是季節性的,則權重也應是季節性的。
小Demo
.
import matplotlib.pyplot as plt
# 加權移動平均法
def wma(list2, w):
n = len(list2)
sum = 0
for i in n:
sum += list2[i] * w[i]
return sum
def answer2(list1, n):
# 加權移動平均法
w = [0.2, 0.3, 0.5] # 各期的權重
listWMA = [] # 加權移動平均值的列表
for i in range(n - 1, len(list1)):
# print(i)
list2 = (list1[i - (n - 1):i + 1])
listWMA.append(ma(list2))
print("加權移動平均值的列表:{}".format(listWMA))
# 最後的移動平均值可做為下一個數的預測
x = listWMA[-1]
print("下一個數的預測:{}".format(x))
# 畫圖
plt.scatter(list(range(len(listWMA))), listWMA)
plt.show()
if __name__ == '__main__':
list1 = [1, 2, 4, 5, 6, 8, 10, 12, 14, 16, 19, 24, 29] # 13個
n = 3 # 移動平均期數
answer2(list1, n) # 加權移動平均法執行結果:
.
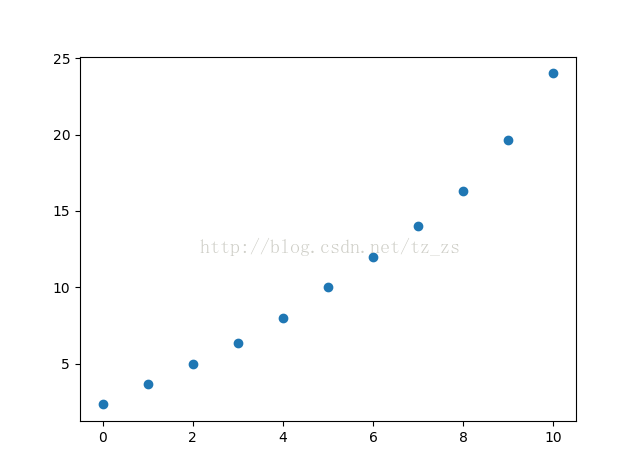
加權移動平均值的列表:[2.3333333333333335, 3.6666666666666665, 5.0, 6.333333333333333, 8.0, 10.0, 12.0, 14.0, 16.333333333333332, 19.666666666666668, 24.0]
下一個數的預測:24.0.
加權移動平均值散點圖:
.
(三)移動平均法的優缺點
使用移動平均法進行預測能平滑掉需求的突然波動對預測結果的影響。但移動平均法運用時也存在著如下問題:
1、 加大移動平均法的期數(即加大n值)會使平滑波動效果更好,但會使預測值對資料實際變動更不敏感;
2、 移動平均值並不能總是很好地反映出趨勢。由於是平均值,預測值總是停留在過去的水平上而無法預計會導致將來更高或更低的波動;
3、 移動平均法要由大量的過去資料的記錄。
二、指數平滑法(Exponential Smoothing,ES)
指數平滑法是布朗(Robert G..Brown)所提出,布朗(Robert G..Brown)認為時間序列的態勢具有穩定性或規則性,所以時間序列可被合理地順勢推延;他認為最近的過去態勢,在某種程度上會持續到最近的未來,所以將較大的權數放在最近的資料。
指數平滑法是生產預測中常用的一種方法。也用於中短期經濟發展趨勢預測,所有預測方法中,指數平滑是用得最多的一種。簡單的全期平均法是對時間數列的過去資料一個不漏地全部加以同等利用;移動平均法則不考慮較遠期的資料,並在加權移動平均法中給予近期資料更大的權重;而指數平滑法則相容了全期平均和移動平均所長,不捨棄過去的資料,但是僅給予逐漸減弱的影響程度,即隨著資料的遠離,賦予逐漸收斂為零的權數。
也就是說指數平滑法是在移動平均法基礎上發展起來的一種時間序列分析預測法,它是通過計算指數平滑值,配合一定的時間序列預測模型對現象的未來進行預測。其原理是任一期的指數平滑值都是本期實際觀察值與前一期指數平滑值的加權平均。
(一)指數平滑法的基本公式
S_t=a\cdot y_t+(1-a)S_{t-1}由該公式可知:式中,
St--時間t的平滑值;
yt--時間t的實際值;
St − 1--時間t-1的平滑值;
a--平滑常數,其取值範圍為[0,1];
1.St是yt和 St − 1的加權算數平均數,隨著a取值的大小變化,決定yt和 St − 1對St的影響程度,當a取1時,St = yt;當a取0時,St = St − 1。
2.St具有逐期追溯性質,可探源至St − t + 1為止,包括全部資料。其過程中,平滑常數以指數形式遞減,故稱之為指數平滑法。指數平滑常數取值至關重要。平滑常數決定了平滑水平以及對預測值與實際結果之間差異的響應速度。平滑常數a越接近於1,遠期實際值對本期平滑值影響程度的下降越迅速;平滑常數a越接近於 0,遠期實際值對本期平滑值影響程度的下降越緩慢。由此,當時間數列相對平穩時,可取較大的a;當時間數列波動較大時,應取較小的a,以不忽略遠期實際值的影響。生產預測中,平滑常數的值取決於產品本身和管理者對良好響應率內涵的理解。
3.儘管St包含有全期資料的影響,但實際計算時,僅需要兩個數值,即yt和 St − 1,再加上一個常數a,這就使指數滑動平均具逐期遞推性質,從而給預測帶來了極大的方便。
4.根據公式S_1=a\cdot y_1+(1-a)S_0,當欲用指數平滑法時才開始收集資料,則不存在y0。無從產生S0,自然無法據指數平滑公式求出S1,指數平滑法定義S1為初始值。初始值的確定也是指數平滑過程的一個重要條件。
如果能夠找到y1以前的歷史資料,那麼,初始值S1的確定是不成問題的。資料較少時可用全期平均、移動平均法;資料較多時,可用最小二乘法。但不能使用指數平滑法本身確定初始值,因為資料必會枯竭。
如果僅有從y1開始的資料,那麼確定初始值的方法有:
1)取S1等於y1;
2)待積累若干資料後,取S1等於前面若干資料的簡單算術平均數,如:S1=(y1+ y2+y3)/3等等。
(二)指數平滑的預測公式
據平滑次數不同,指數平滑法分為:一次指數平滑法、二次指數平滑法和三次指數平滑法等。
(1) 一次指數平滑預測
當時間數列無明顯的趨勢變化,可用一次指數平滑預測。其預測公式為:
yt+1'=ayt+(1-a)yt'
式中,
yt+1'--t+1期的預測值,即本期(t期)的平滑值St ;
yt--t期的實際值;
yt'--t期的預測值,即上期的平滑值St-1 。
該公式又可以寫作:yt+1'=yt'+a(yt- yt')。可見,下期預測值又是本期預測值與以a為折扣的本期實際值與預測值誤差之和。
(2) 二次指數平滑預測
二次指數平滑是對一次指數平滑的再平滑。它適用於具線性趨勢的時間數列。其預測公式為:yt+m=(2+am/(1-a))yt'-(1+am/(1-a))yt=(2yt'-yt)+m(yt'-yt) a/(1-a)
顯然,二次指數平滑是一直線方程,其截距為:(2yt'-yt),斜率為:(yt'-yt) a/(1-a),自變數為預測天數。式中,
yt= ayt-1'+(1-a)yt-1
(3) 三次指數平滑預測
三次指數平滑預測是二次平滑基礎上的再平滑。其預測公式是:
yt+m=(3yt'-3yt+yt)+[(6-5a)yt'-(10-8a)yt+(4-3a)yt]*am/2(1-a)2+ (yt'-2yt+yt')*a2m2/2(1-a)2
式中,
yt=ayt-1+(1-a)yt-1
它們的基本思想都是:預測值是以前觀測值的加權和,且對不同的資料給予不同的權,新資料給較大的權,舊資料給較小的權。
(三)指數平滑法的趨勢調整
一段時間內收集到的資料所呈現的上升或下降趨勢將導致指數預測滯後於實際需求。通過趨勢調整,新增趨勢修正值,可以在一定程度上改進指數平滑預測結果。調整後的指數平滑法的公式為:
包含趨勢預測(YITt)=新預測(Yt)+趨勢校正(Tt)
進行趨勢調整的指數平滑預測有三個步驟:
1、 利用前面介紹的方法計算第t期的簡單指數平滑預測(Yt);
2、 計算趨勢。其公式為: Tt=(1-b)Tt-1+b(Yt-Yt-1)其中,
Tt=第t期經過平滑的趨勢;
Tt-1=第t期上期經過平滑的趨勢;
b=選擇的趨勢平滑係數;
Yt=對第t期簡單指數平滑預測;
Yt-1=對第t期上期簡單指數平滑預測。
3、計算趨勢調整後的指數平滑預測值(YITt)。計算公式為:YITt=Yt+Tt。
.
import matplotlib.pyplot as plt
# 一次指數平滑預測
def es1(list3, t, a):
if t == 0:
return list3[0] # 初始的平滑值取實際值
return a * list3[t - 1] + (1 - a) * es1(list3, t - 1, a) # 遞迴呼叫 t-1 → 12
# 二次指數平滑預測
def es2(list3, t, a):
if t == 0:
return list3[0]
return (a * es2(list3, t - 1, a) + (1 - a) * list3[t - 1])
def answer3(list2):
# 指數平滑法
a = 0.8 # 平滑常數
listES = [] # 指數平滑值的列表
for i in range(len(list2)):
if i == 0:
listES.append(list2[i])
continue
s = a * list2[i] + (1 - a) * listES[-1]
listES.append(s)
print("指數平滑值的列表:{}".format(listES))
# 畫圖
plt.scatter(list(range(len(listES))), listES)
plt.show()
# 一次指數平滑預測
t = len(list2) # 預測的時期 13
x = es1(list2, t, a)
print("下一個數的一次指數平滑預測:{}".format(x))
# 二次指數平滑預測
m = 3 # 預測的值為之後的第m個
yt = es2(list2, t - 1, a)
ytm = listES[t - 2]
esm = ((2 * ytm - yt) + m * (ytm - yt) * a / (1 - a))
print("之後的第{}個數的二次指數平滑預測:{}".format(m, esm))
if __name__ == '__main__':
list1 = [1, 2, 4, 5, 6, 8, 10, 12, 14, 16, 19, 24, 29] # 13個
n = 3 # 移動平均期數
answer3(list1) # 指數平滑法
執行結果:
.
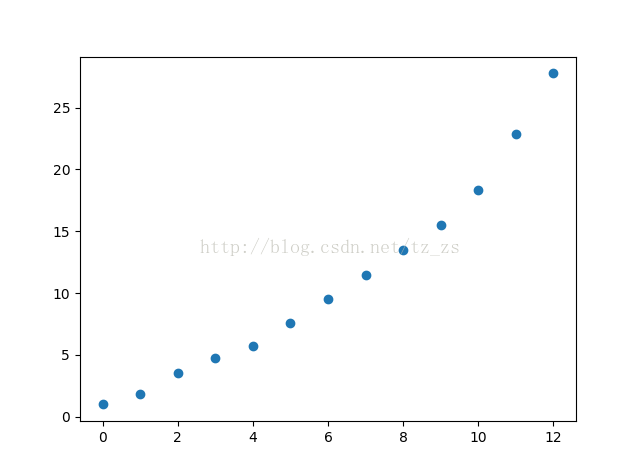
指數平滑值的列表:[1, 1.8, 3.56, 4.712, 5.742400000000001, 7.5484800000000005, 9.509696, 11.5019392, 13.50038784, 15.500077568, 18.300015513600002, 22.860003102720004, 27.772000620544002]
下一個數的一次指數平滑預測:27.772000620544002
之後的第3個數的二次指數平滑預測:137.5839514214401.
指數平滑值的散點圖:
.