OpenCV計算機視覺學習(4)——影象平滑處理(均值濾波,高斯濾波,中值濾波,雙邊濾波)
如果需要處理的原圖及程式碼,請移步小編的GitHub地址
傳送門:請點選我
如果點選有誤:https://github.com/LeBron-Jian/ComputerVisionPractice
“平滑處理”(smoothing)也稱“模糊處理”(bluring),是一項簡單且使用頻率很高的影象處理方法。平滑處理的用途有很多,最常見的是用來減少影象上的噪點或者失真。在涉及到降低影象解析度時,平滑處理是非常好用的方法。
影象濾波,就是在儘量保留影象細節特徵的條件下對目標影象的噪聲進行抑制,是影象預處理中不可或缺的操作,其處理效果的好壞將直接影響到後續影象處理和分析的有效性和可靠性。
關於濾波,一種形象的比喻法是:我們可以把濾波器想象成一個包含加權係數的視窗,當使用這個濾波器平滑處理影象時,就把這個視窗放到影象之上,透過這個視窗來看我們得到的影象。而對濾波處理的要求有兩個,一是不能損壞影象的輪廓及邊緣等重要資訊;二是使影象清晰視覺效果好。
在學習這幾種濾波之前,我們首先記住兩句話:
- 1,濾波是掩膜(mask)和影象的卷積。
- 2,濾波過程分為:(1)計算掩膜 (2)卷積 ——掩膜上每一個位置的值和影象上對應位置的畫素值的乘加運算。
這裡對幾個濾波函式做一下筆記,下面這兩個圖呢,是盜的,主要是人家寫的好。哈哈哈哈,侵刪啊!
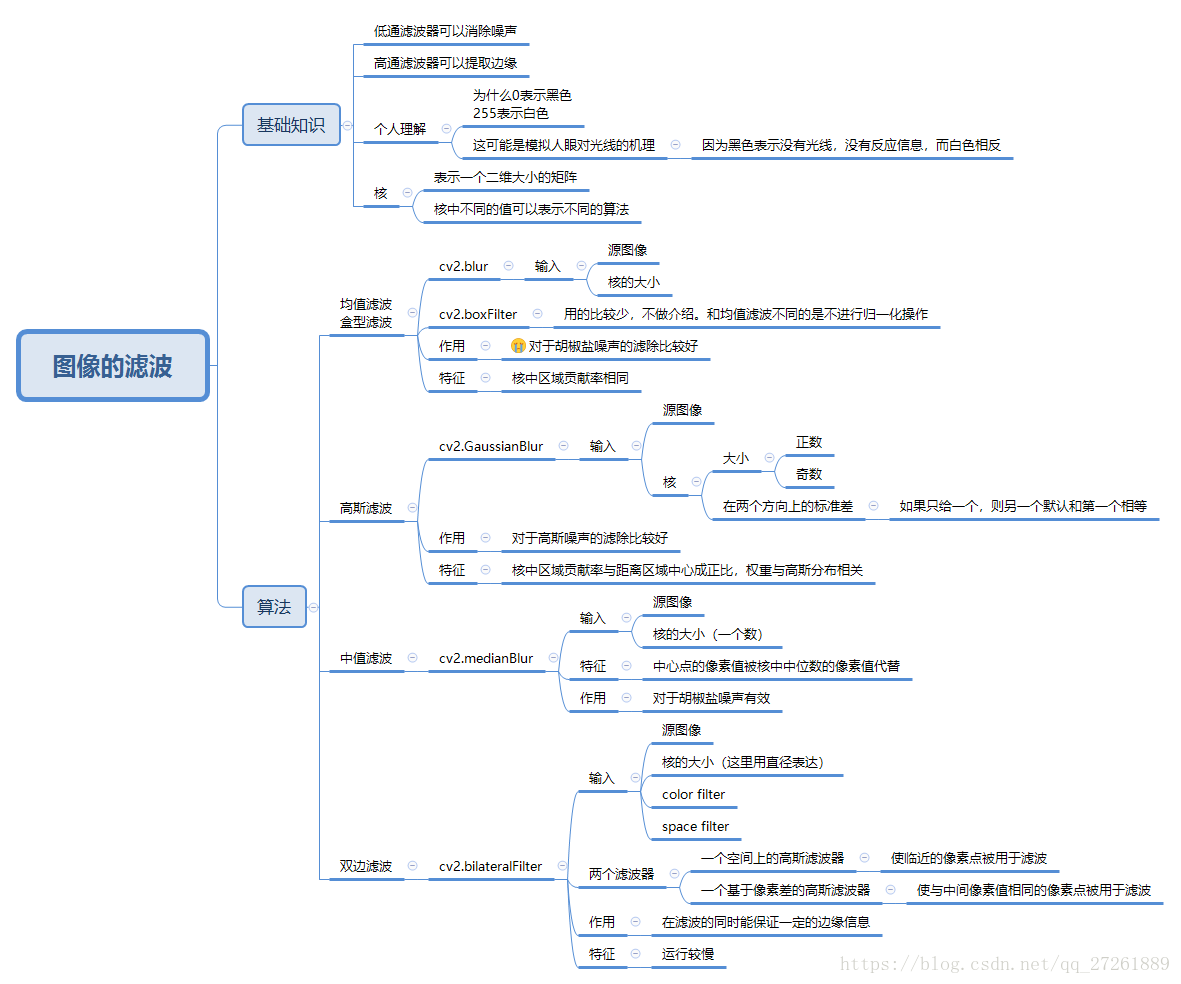
具體模糊和濾波的關係如下圖(https://www.zhihu.com/question/54918332/answer/142137732):

1,均值濾波(Mean Filtering)
均值濾波(低通濾波)是典型的線性濾波演算法,它是指在影象上對目標畫素給一個模板,該模板包括了其周圍的臨近畫素(以目標畫素為中序的周圍八個畫素,構成一個濾波模板,即去掉目標畫素本身),再用模板中的全體畫素的平均值來代替原來畫素值。
簡單來說,圖片中一個方塊區域 N*M 內,中心點的畫素為全部點畫素值的平均值。均值濾波就是對整張圖片進行以上操作。
我們可以看下圖的矩陣進行理解:

進而我們可以看下圖(盜圖,侵刪https://blog.csdn.net/Eastmount/article/details/82216380),紅色點的畫素值為藍色背景區域畫素值之和除25。
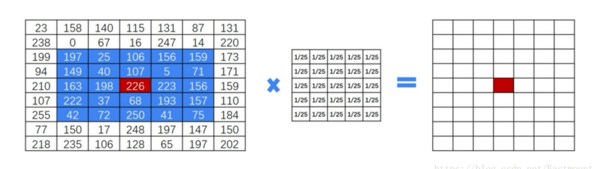
其中紅色區域的畫素值均值濾波處理過程為: ((197+25+106+156+159)+ (149+40+107+5+71)+ (163+198+226+223+156)+ (222+37+68+193+157)+ (42+72+250+41+75)) / 25 = 125.52
其中5*5的矩陣稱為核,針對原始影象內的畫素點,採用核進行處理,得到結果影象。

提取1/25 可以將核轉換為如下形式:

就是我們上面的公式。
1.1,均值濾波函式Blur
Python呼叫OpenCV實現均值濾波的核心函式如下:
blur(src, ksize, dst=None, anchor=None, borderType=None)
引數詳情:
- src引數表示待處理的輸入影象。
- ksize引數表示模糊核心大小。比如(1,15)表示生成的模糊核心是一個1*15的矩陣。
- dst引數表示輸出與src相同大小和型別的影象。
- anchor引數、borderType引數可忽略
其中,核大小是以(寬度,高度)表示的元組形式。常見的形式包括:和大小(3, 3)和(5, 5):
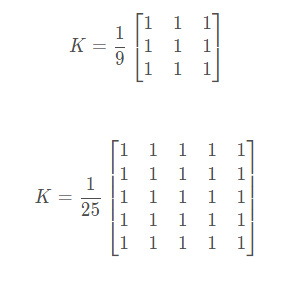
均值濾波實現程式碼如下:
#_*_coding:utf-8_*_
import cv2
import matplotlib.pyplot as plt
def blur_filter_func(filename):
img = cv2.imread(filename)
rgbimg = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
# 均值濾波: 簡單的平均卷積操作
result = cv2.blur(img, (5, 5))
# 顯示影象
titles = ['origin image', 'blur image']
images = [rgbimg, result]
for i in range(2):
plt.subplot(1, 2, i+1), plt.imshow(images[i])
plt.title(titles[i])
plt.xticks([]), plt.yticks([])
plt.show()
if __name__ == '__main__':
filename = 'lenaNoise.png'
blur_filter_func(filename)
效果如下:

1.2,均值濾波優缺點
優點:
效率高,思路簡單
缺點:
均值濾波本身存在著固有的缺陷,即它不能很好地保護影象細節,在影象去噪的同時也破壞了影象的細節,從而使影象變得模糊,不能很好地去除噪聲點,特別是椒鹽噪聲。
這就要開始提到我們的高斯濾波了。
高斯濾波器是一種現性濾波器,能夠有效地抑制噪聲,平滑影象。其作用原理和均值濾波器類似,都是取濾波器視窗內畫素的均值作為輸出。其視窗模板的稀疏和均值濾波器不同,均值濾波器的模板稀疏都是相同的為1;而高斯濾波器的模板稀疏,則隨著距離模板中心的增大而係數減少。所以,高斯濾波器相比於均值濾波器對影象的模型程度較小。
1.3 方框濾波(盒子濾波)
方框濾波比均值濾波多一個引數。此引數為normalize,當 normalize=True時,與均值濾波結果相同,normalize=False,表示對加和後的結果不進行平均操作,大於255的使用255表示。
方框濾波BoxFilter()的實現程式碼:
def BoxFilter(Imge,dim,dim2,flag): #Image為待處理影象,dim為濾波器的大小dim*dim2
im=array(Imge)
#序列化
sigema=0
#濾波求和
for i in range(int(dim/2), im.shape[0] - int(dim/2)):
for j in range(int(dim2/2), im.shape[1] - int(dim2/2)):
for a in range(-int(dim/2), -int(dim/2)+dim):
for b in range(-int(dim2/2), -int(dim2/2)+dim2):
sigema = sigema + img[i + a, j + b]
#對於濾波範圍內求和,從左到右,從上到下掃
if(flag):
im[i, j] = sigema / (dim*dim2)
else:
im[i,j]=min(sigema,255)
#歸一化則與均值濾波一致,不歸一化的話超過255用255表示
sigema = 0
#濾波移動
return im
原文連結:https://blog.csdn.net/zjyang12345/java/article/details/103358260
用途:非歸一化(normalized = False)的方框濾波用於計算每個畫素領域內的積分特性,比如密集光流演算法(dense optical flow algorithms)中用到的影象倒數的協方差矩陣(convariance matrices of image derivatives)。
選擇歸一化後,方框濾波與均值濾波結果相同,不選擇容易越界,越界的話,超過255則用255表示。
下面使用OpenCV程式碼實現:
#_*_coding:utf-8_*_
import cv2
import matplotlib.pyplot as plt
def box_blur_filter_func(filename):
img = cv2.imread(filename)
rgbimg = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
blur = cv2.blur(img, (3, 3))
# 方框濾波: 基本和均值濾波一樣,可以選擇歸一化,如果選擇歸一化,則和均值濾波一樣
# 如果不選擇歸一化,則方框濾波容易越界,越界的話,超過255則用255表示
result_normal = cv2.boxFilter(img, -1, (3, 3), normalize=True)
result_nonormal = cv2.boxFilter(img, -1, (3, 3), normalize=False)
# 顯示影象
titles = ['origin image', 'boxFilter image no normalize', 'boxFilter image normalize', 'blut filter image']
images = [rgbimg, result_nonormal, result_normal, blur]
for i in range(4):
plt.subplot(2, 2, i+1), plt.imshow(images[i])
plt.title(titles[i])
plt.xticks([]), plt.yticks([])
plt.show()
if __name__ == '__main__':
filename = 'lenaNoise.png'
box_blur_filter_func(filename)
效果圖如下:

2,高斯濾波(高斯模糊)(Gaussian Filtering)
通常,影象處理軟體會提供“模糊”(blur)濾鏡,使圖片產生模糊的效果。“模糊”的演算法有很多種,這裡我們首先學習“高斯模糊”(Gaussian Blur)。它將正態分佈(“高斯分佈”)用於影象處理中。本質上,高斯濾波是一種資料平滑的技術(data smoothing),適用於多個場景,影象處理恰好提供了一個直觀的應用例項。
2.1,高斯濾波的原理
(PS:其實高斯濾波和高斯模糊是一個意思,為什麼叫高斯模糊呢,就是這個濾波的效果看起來像是把影象給弄模糊了,所以又有了“高斯模糊”的叫法,而後面為了統一,這裡我都叫高斯濾波)
既然認真學習原理了,這裡我們首先對高斯函式做一個認真的學習。
高斯分佈其實學名叫正態分佈(Normal distribution),正態曲線呈鍾型,兩頭低,中間高,左右對稱因其曲線呈鐘形,因此人們又經常稱之為鐘形曲線。
高斯分佈公式如下:

其中,μ是x的均值,σ是x的方差。因為計算平均值的時候,中心點就是原點,所以μ等於0。

根據一維高斯函式,可以推匯出二維高斯函式:

形狀如下:
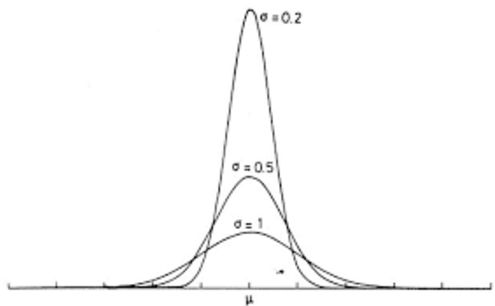
上圖為一維高斯分佈示意圖, μ 覺得了分佈對稱中心, σ 決定了分佈的形狀, σ 越小形狀越瘦小, σ 越大越矮胖。所以就是越接近中心,取值越大,越遠離中心,取值越小。計算平均值的時候,我們只需要將“中心點”作為原點,其他店按照其在正態曲線上的位置,分配權重,就可以得到一個加權平均值。
那高斯分佈公式的作用到底是什麼呢?——計算高斯濾波用的掩膜(mask)。
掩膜是什麼呢?下面我們首先來一個3*3的均值濾波的掩膜:
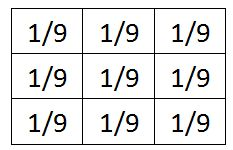
可以看到,均值掩膜內所有稀疏均相等,為1/9,且他們的和為1,同理可得5*5均值濾波的掩膜。在“中間點” 取“周圍點” 的平均值,就變為周圍的平均值了,在數值上,這是一種“平滑化”,在圖形上,就相當於產生“模糊”效果,“中間點” 失去細節。顯然,計算平均值時,取值範圍越大,“模糊效果”越強烈。
這裡我們分析了均值濾波,後面學到均值濾波的時候就略過了。
下面計算權重矩陣。
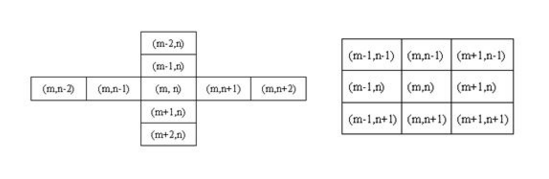
對於影象中任意一點(x, y),它周圍的座標為:(這裡直接盜圖,方便)
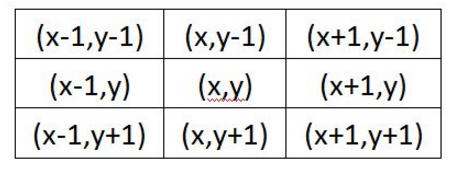
例如:要產生一個高斯濾波模板,以模板的中心位置為座標原點進行取樣。模板在各個位置的座標,如下圖所示(x軸水平向右,y軸豎直向下),我們用數值代替上面(x, y),假定中心點的座標為(0, 0),那麼距離它周圍的八個點的座標如下:

更遠的點,依次類推,為了計算權重矩陣,需要設定 σ 的值,假定 σ = 1.5 ,則模糊半徑為1的權重矩陣如下:
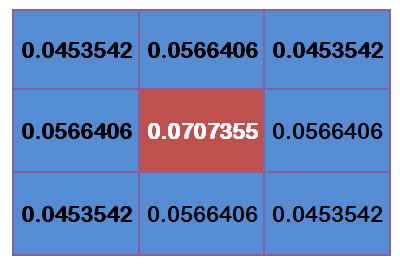
這九個點的權重綜合等於 0.4787147,如果只計算這 9 個點的加權平均,還必須讓他們的權重之和等於1,因此上面的九個值還要分別除以 0.4787147,得到最終的權重矩陣:
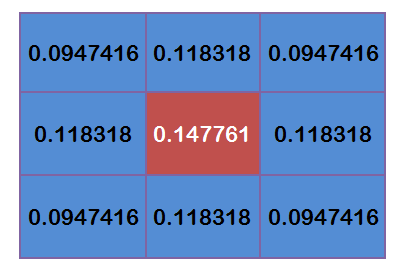
有了權重矩陣,就可以計算高斯模糊的值了。假設現有九個畫素點,灰度值(0-255)如下:
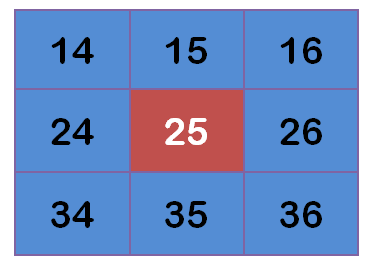
每個點乘以自己的權重值:

得到:
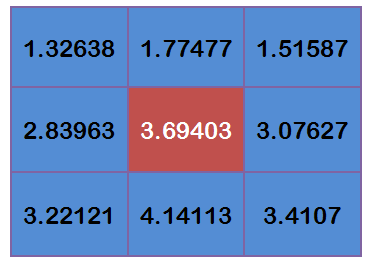
將這九個值加起來,就是中心點的高斯模糊的值,對所有的點重複這個過程,就得到了高斯模糊後的影象。如果原圖是彩色的影象,可以對RBG三個通道分別做高斯模糊。
(PS:非常感謝https://blog.csdn.net/jiandanjinxin/article/details/51281828這篇部落格做的圖)
最後再在網上盜個圖,展示下利用高斯掩膜和影象進行卷積求解高斯模糊:
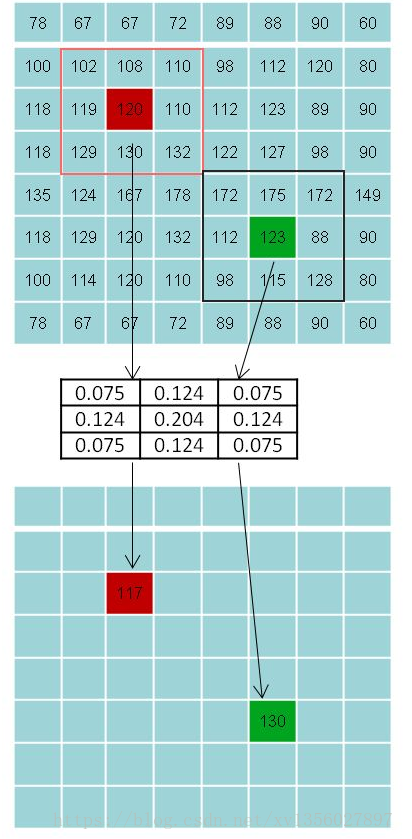
117 = 102 * 0.075 + 108 * 0.124 + 110 * 0.075 +119 * 0.124 + 120 * 0.204 + 110 * 0.124+129 * 0.075 + 130 * 0.124 + 132 * 0.075
130 = 172 * 0.075 + 175 * 0.124 + 172 * 0.075 +112 * 0.124 + 123 * 0.204 + 88 * 0.124 +98* 0.075 + 115 * 0.124 + 128 * 0.075
所有畫素都用圖上的那一套模板進行卷積運算,最終得到濾波的結果。這樣就可以讓一個完整的高斯濾波的原理展示出來,我也理解了,謝謝各位網友。
這樣計算出來的模板有兩種形式:小數和整數
1,小數形式的模板,就是直接計算得到的值,沒有經過任何的處理
2,整數形式的模板,則需要進行歸一化,將模板左上角的值歸一化為1
2.2,高斯濾波函式GaussianBlur
函式原型:
GaussianBlur(src, ksize, sigmaX, dst=None, sigmaY=None, borderType=None)
變數的含義:
- src引數表示待處理的輸入影象。
- ksize引數表示高斯濾波器模板大小。 ksize.width和ksize.height可以不同,但它們都必須是正數和奇數。或者,它們可以是零,即(0, 0),然後從σ計算出來。
- sigmaX引數表示 X方向上的高斯核心標準差。
- sigmaY引數表示 Y方向上的高斯核心標準差。 如果sigmaY為零,則設定為等於sigmaX,如果兩個sigma均為零,則分別從ksize.width和ksize.height計算得到。
補:若ksize不為(0, 0),則按照ksize計算,後面的sigmaX沒有意義。若ksize為(0, 0),則根據後面的sigmaX計算ksize。
比如常用的如下:
blurred = cv2.GaussianBlur(gray, (9, 9),0)
高斯模糊本質上是低通濾波器,輸出影象的每個畫素點是原影象上對應畫素點與周圍畫素點的加權和。
高斯矩陣的尺寸和標準差:(9, 9)表示高斯矩陣的長和寬,標準差取0時,OpenCV會根據高斯矩陣的尺寸自己計算,高斯矩陣的尺寸越大,標準差越大,處理過的影象模糊程度越大。
高斯平滑與簡單平滑不同,它在對領域內畫素進行平均時,給與不同位置的畫素不同的權值,下面所示的是 3*3 和 5*5 領域的高斯模板。
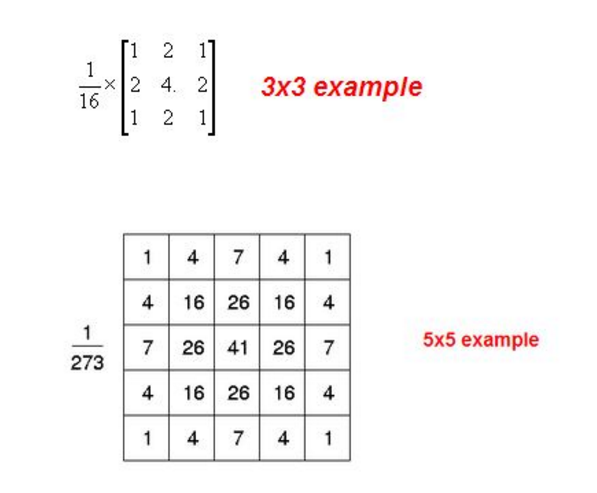

程式碼如下:
#_*_coding:utf-8_*_
import cv2
import matplotlib.pyplot as plt
def gaussian_blur_func(filename):
img = cv2.imread(filename)
rgbimg = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
# 高斯濾波:高斯模糊的卷積核的數值是滿足高斯分佈的,相當於更重視中間的
# 標準差取0時,OpenCV會根據高斯矩陣的尺度自己計算
result1 = cv2.GaussianBlur(img, (5, 5), 0)
result2 = cv2.GaussianBlur(img, (5, 5), 1)
# 顯示影象
titles = ['origin image', 'gaussian blur image stu 0', 'gaussian blur image stu 1']
images = [rgbimg, result1, result2]
for i in range(3):
plt.subplot(1, 3, i+1), plt.imshow(images[i])
plt.title(titles[i])
plt.xticks([]), plt.yticks([])
plt.show()
if __name__ == '__main__':
filename = 'lenaNoise.png'
gaussian_blur_func(filename)
效果圖如下:

其實理解了過程,我們也可以自己寫出高斯濾波的原始碼,簡單來說就是歸一化,灰度化,然後遍歷灰度影象素點,對響度點領域進行高斯濾波,這裡就不寫了,直接展示程式碼。
程式碼如下:
import cv2 as cv
import math
import numpy as np
# 灰度化處理
def rgb2gray(img):
h=img.shape[0]
w=img.shape[1]
img1=np.zeros((h,w),np.uint8)
for i in range(h):
for j in range(w):
img1[i,j]=0.144*img[i,j,0]+0.587*img[i,j,1]+0.299*img[i,j,1]
return img1
# 計算高斯卷積核
def gausskernel(size):
sigma=1.0
gausskernel=np.zeros((size,size),np.float32)
for i in range (size):
for j in range (size):
norm=math.pow(i-1,2)+pow(j-1,2)
gausskernel[i,j]=math.exp(-norm/(2*math.pow(sigma,2))) # 求高斯卷積
sum=np.sum(gausskernel) # 求和
kernel=gausskernel/sum # 歸一化
return kernel
# 高斯濾波
def gauss(img):
h=img.shape[0]
w=img.shape[1]
img1=np.zeros((h,w),np.uint8)
kernel=gausskernel(3) # 計算高斯卷積核
for i in range (1,h-1):
for j in range (1,w-1):
sum=0
for k in range(-1,2):
for l in range(-1,2):
sum+=img[i+k,j+l]*kernel[k+1,l+1] # 高斯濾波
img1[i,j]=sum
return img1
image = cv.imread("lenaNoise.png")
grayimage=rgb2gray(image)
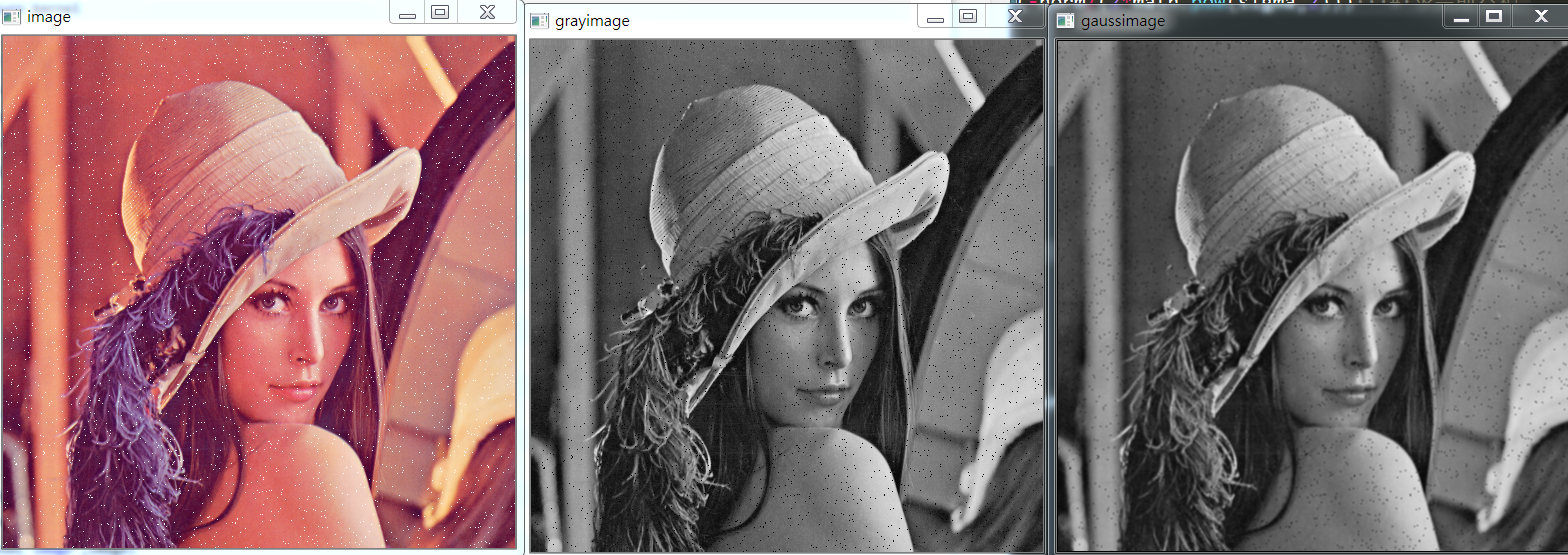
gaussimage = gauss(grayimage)
cv.imshow("image",image)
cv.imshow("grayimage",grayimage)
cv.imshow("gaussimage",gaussimage)
cv.waitKey(0)
cv.destroyAllWindows()
效果圖如下:
3,雙邊濾波
雙邊濾波其實很簡單,它只是比高斯濾波多了一種掩膜而已。兩種掩膜都是套用高斯分佈公式得到的。雙邊濾波不光考慮了畫素在空間中位置遠近程度的影響,還考慮了畫素亮度相近程度的影響。
雙邊濾波(Bilateral filter)是一種非線性的濾波方法,是結合影象的空間鄰近度和畫素值相似度的一種折中處理,同時考慮空域資訊和灰度相似性,達到保邊去噪的目的。雙邊濾波器顧名思義比高斯濾波多了一個高斯方差sigma-d,它是基於空間分佈的高斯濾波函式,所以在邊緣附近,離的較遠的畫素不會太多影響到邊緣上的畫素值,這樣就保證了邊緣附近畫素值的儲存。但是由於儲存了過多的高頻資訊,對於彩色影象裡的高頻噪聲,雙邊濾波器不能夠乾淨的濾掉,只能夠對於低頻資訊進行較好的濾波。
雙邊濾波在濾波的同時能保證一定的邊緣資訊,但是執行較慢。
3.1雙邊濾波函式(BilateralFilter )
函式如下:
bilateralFilter(src, d, sigmaColor, sigmaSpace, dst=None, borderType=None)
引數如下:
- src引數表示待處理的輸入影象。
- d引數表示在過濾期間使用的每個畫素鄰域的直徑。如果輸入d非0,則sigmaSpace由d計算得出,如果sigmaColor沒輸入,則sigmaColor由sigmaSpace計算得出。
- sigmaColor引數表示色彩空間的標準方差,一般儘可能大。較大的引數值意味著畫素鄰域內較遠的顏色會混合在一起,從而產生更大面積的半相等顏色。
- sigmaSpace引數表示座標空間的標準方差(畫素單位),一般儘可能小。引數值越大意味著只要它們的顏色足夠接近,越遠的畫素都會相互影響。當d > 0時,它指定鄰域大小而不考慮sigmaSpace。 否則,d與sigmaSpace成正比。
實現程式碼如下:
#_*_coding:utf-8_*_
import cv2
import matplotlib.pyplot as plt
def bilateral_filter_func(filename):
img = cv2.imread(filename)
rgbimg = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
# 雙邊濾波:它能保持邊界清晰的情況下有效的去除噪聲,但是這種操作比較慢
# 雙邊濾波擁有美顏的效果
bilateral_filter = cv2.bilateralFilter(img, d=0, sigmaColor=100, sigmaSpace=15)
# 顯示影象
titles = ['origin image', 'bilteral filter image']
images = [rgbimg, bilateral_filter]
for i in range(2):
plt.subplot(1, 2, i+1), plt.imshow(images[i])
plt.title(titles[i])
plt.xticks([]), plt.yticks([])
plt.show()
if __name__ == '__main__':
filename = 'lenaNoise.png'
bilateral_filter_func(filename)
效果如下:

4,中值濾波(Median Filtering)
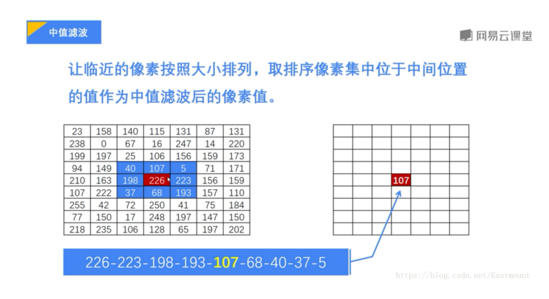
中值濾波是一種非線性數字濾波器技術,經常用於去除影象或者其他訊號中的噪聲,是處理椒鹽噪聲的常用降噪演算法。中值濾波將每一畫素點的灰度值設定為該點某領域視窗內的所有畫素點灰度值的中值。
在使用鄰域平均法去噪的同時也使得邊界變得模糊。而中值濾波是非線性的影象處理方法,在去噪的同時可以兼顧到邊界資訊的保留。選一個含有奇數點的視窗W,將這個視窗在影象上掃描,把視窗中所含的畫素點按灰度級的升或降序排列,取位於中間的灰度值來代替該點的灰度值。 例如選擇濾波的視窗如下圖,是一個一維的視窗,待處理畫素的灰度取這個模板中灰度的中值,濾波過程如下:
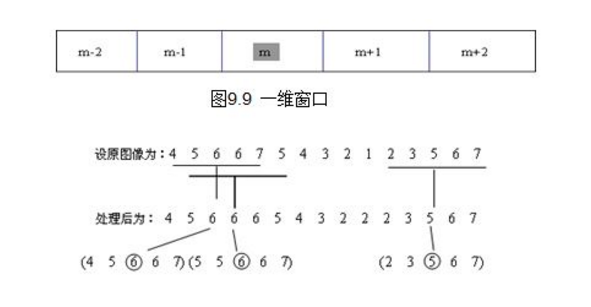
影象平滑裡中值濾波的效果最好。
4.1,中值濾波函式(MedianBlur )
OpenCV主要呼叫函式如下:
medianBlur(src, ksize, dst=None)
引數意義:
- src引數表示待處理的輸入影象。
- ksize引數表示濾波視窗尺寸,必須是奇數並且大於1。比如這裡是5,中值濾波器就會使用5×5的範圍來計算,即對畫素的中心值及其5×5鄰域組成了一個數值集,對其進行處理計算,當前畫素被其中值替換掉。
- dst引數表示輸出與src相同大小和型別的影象。
程式碼如下:
#_*_coding:utf-8_*_
import cv2
import matplotlib.pyplot as plt
def median_blur_filter_func(filename):
img = cv2.imread(filename)
rgbimg = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
# 中值濾波: 相當於用中值代替
median = cv2.medianBlur(img, 5)
# 顯示影象
titles = ['origin image', 'blut filter image']
images = [rgbimg, median]
for i in range(2):
plt.subplot(1, 2, i+1), plt.imshow(images[i])
plt.title(titles[i])
plt.xticks([]), plt.yticks([])
plt.show()
if __name__ == '__main__':
filename = 'lenaNoise.png'
median_blur_filter_func(filename)
效果如下:

4.2,視窗問題
中值濾波降噪的原理為使用噪點的某一個鄰域內的中值代替該噪點,鄰域範圍越大則邊緣保留效果越差,從視覺上來看,即更加模糊,但降噪效果明顯。此外,鄰域亦即視窗的形狀也會影響降噪的效果。通常有3*3 5*5 ,十字形,圓形等。這裡此文采用十字形
常用的視窗還有方形、十字形、圓形和環形。不同形狀的視窗產生不同的濾波效果,方形和圓形視窗適合外輪廓線較長的物體影象,而十字形視窗對有尖頂角狀的影象效果好。中值濾波對於消除孤立點和線段的干擾十分有用,尤其是對於二進噪聲,但對消除高斯噪聲的影響效果不佳。對於一些細節較多的複雜影象,可以多次使用不同的中值濾波。
程式碼如下:
import numpy as np
import random
def median_filtering(input_signal):
'''
中值濾波(適用於灰度圖)
如:
- + -
+ * +
- + -
* 為噪點,濾波方法為:取4個+的中位數(若某+不在輸入訊號範圍內,則隨機新增0或255)
:param input_signal: 輸入訊號矩陣(2D)
:return: 濾波後的訊號
'''
salt_pepper = [0, 255]
m, n = input_signal.shape # 獲取輸入圖片的尺寸(行和列)
input_signal_cp = input_signal.copy() # 輸入訊號的副本
nosiy_data_around = [] # 存放噪點上下左右的資料點
# 遍歷濾波
for i in range(m):
for j in range(n):
# 當灰度值為0或255時,則認為該資料點為椒鹽噪點
if input_signal_cp[i, j] == 255 or input_signal_cp[i, j] == 0:
# 每次無效資料點(即不再範圍內)為4,每有一個在範圍內,即-1
invalid_data_per = 4
if i + 1 < n:
nosiy_data_around.append(input_signal_cp[i + 1, j])
invalid_data_per = invalid_data_per - 1
if i - 1 >= 0:
nosiy_data_around.append(input_signal_cp[i - 1, j])
invalid_data_per = invalid_data_per - 1
if j + 1 < m:
nosiy_data_around.append(input_signal_cp[i, j + 1])
invalid_data_per = invalid_data_per - 1
if j - 1 >= 0:
nosiy_data_around.append(input_signal_cp[i, j - 1])
invalid_data_per = invalid_data_per - 1
else:
if invalid_data_per > 0:
# 根據無效資料點的個數,隨機新增0或255
for k in range(invalid_data_per):
nosiy_data_around.append(salt_pepper[random.randint(0, 1)])
# 取中位數
input_signal_cp[i, j] = np.median(nosiy_data_around)
# 該噪點的周圍資料陣列清空,為下一個噪點周圍資料存在做準備
nosiy_data_around = []
return input_signal_cp
5,幾種濾波的程式碼實現
程式碼如下:
import numpy as np
import cv2
import matplotlib.pyplot as plt
######## 四個不同的濾波器 #########
img = cv2.imread('cat.jpg')
# 均值濾波
img_mean = cv2.blur(img, (5,5))
# 高斯濾波
img_Guassian = cv2.GaussianBlur(img,(5,5),0)
# 中值濾波
img_median = cv2.medianBlur(img, 5)
# 雙邊濾波
img_bilater = cv2.bilateralFilter(img,9,75,75)
# 展示不同的圖片
titles = ['srcImg','mean', 'Gaussian', 'median', 'bilateral']
imgs = [img, img_mean, img_Guassian, img_median, img_bilater]
for i in range(5):
plt.subplot(2,3,i+1)#注意,這和matlab中類似,沒有0,陣列下標從1開始
plt.imshow(imgs[i])
plt.title(titles[i])
plt.show()
效果圖如下:

6,椒鹽噪聲與中值濾波的Python實現與檢驗
6.1 椒鹽噪聲(Salt Pepper Noise)
椒鹽噪聲也稱為脈衝雜訊,是影象中經常見到的一種雜訊,它是一種隨機出現的白電或者黑點,可能是亮的區域有黑色畫素或是在暗的區域有白色畫素(或者兩者皆有)——維基百科
關於椒鹽噪聲的幾點注意
- 噪聲型別隨機,即亮斑或暗斑(對應灰度圖0,255)
- 噪聲概率為先驗概率(如噪聲概率為0.1,資料點總數為1000),而實際的噪聲點並不一定為10,
6.2 椒鹽噪聲實現演算法思路
- 1,新建一個與輸入影象等長的陣列
- 2,陣列中存放(1,100/(100*noisy probability))的隨機整數
- 3,當上述陣列中出現的值為1時,則認為對應的資料點為噪點
- 4,該噪點等概率的取亮斑或暗斑(0, 255)
程式碼如下:
import numpy as np
import random
def salt_pepper(intput_signal, probability):
'''
椒鹽噪聲演算法(適用於灰度圖)
:param intput_signal: 輸入訊號矩陣(2D)
:param probability: 噪聲概率(如:0.1為10%)
:return: 加噪後的影象、實際噪點數、理論噪點數
'''
nisy = [0, 255] # 噪聲(salt, papper)
m, n= intput_signal.shape # 獲取輸入圖片尺寸(行和列)
intput_signal_cp = intput_signal.copy() # 輸入訊號的副本
intput_signal_cp = intput_signal_cp.reshape(-1) # reshape為一個行向量
# 該噪聲概率下,理論上noisy_data_probability_num個數據點中1一個噪點
noisy_data_probability_num = int(100 / (probability * 100))
# 噪點陣列,當陣列中的值為1時,則認為對應的資料點為噪點
noisy_data = []
for i in range(m*n):
noisy_data.append(random.randint(1, noisy_data_probability_num))
# 實際噪點數與理論噪點數
actual_noisy_data_num = 0
theory_noisy_data_num = int(m * n * probability)
# 新增噪點
for i in range(m*n):
if noisy_data[i] == 1:
actual_noisy_data_num = actual_noisy_data_num + 1
intput_signal_cp[i] = nisy[random.randint(0, 1)]
# 重塑至m*n的矩陣
intput_signal_cp = intput_signal_cp.reshape(m, n)
return intput_signal_cp, actual_noisy_data_num, theory_noisy_data_num
6.3 中值濾波抑制噪聲
受光照、氣候、成像裝置等因素的影響,灰度化後的影象存在噪聲和模糊干擾,直接影響到下一步的文字識別,因此,需要對影象進行增強處理。圖片預處理中重要一環就是椒鹽去澡,通常用到中值濾波器進行處理,效果很好。中值濾波器是一種非線性濾波器,其基本原理是把數字影象中某點的值用其領域各點值的中值代替。如求點[i,j]的灰度值計算方法為:(1)按灰度值順序排列[i,j]領域中的畫素點;(2)取排序畫素集的中間值作為[i,j]的灰度值。中值濾波技術能有效抑制噪聲。
直接上程式碼,希望給大家有幫助:
import numpy as np
import cv2
import tensorflow as tf
from PIL import Image
import os
import scipy.signal as signal
input_images = np.zeros((300, 300))
filename = "D:\字母相簿\F\P80627-112853.jpg"
print(filename)
img = Image.open(filename).resize((300, 300)).convert('L')
width = img.size[0]
height = img.size[1]
for h in range(0, height):
for w in range(0, width):
if img.getpixel((h, w)) < 128:
input_images[w, h] = 0
else:
input_images[w, h] = 1
cv2.imshow("test1111", input_images)
data = signal.medfilt2d(np.array(img), kernel_size=3) # 二維中值濾波
for h in range(0, height):
for w in range(0, width):
if data[h][w] < 128:
input_images[w, h] = 0
else:
input_images[w, h] = 1
cv2.imshow("test2222", input_images)
data = signal.medfilt2d(np.array(img), kernel_size=5) # 二維中值濾波
for h in range(0, height):
for w in range(0, width):
if data[h][w] < 128:
input_images[w, h] = 0
else:
input_images[w, h] = 1
cv2.imshow("test3333", input_images)
cv2.waitKey(0)
6.4 高斯噪聲的Python實現
在處理影象的時候,有時候可能我們需要給影象新增高斯噪聲或者椒鹽噪聲,下面學習一下如何新增高斯噪聲和椒鹽噪聲的程式碼。
首先,我們先定義高斯噪聲函式 GaussianNoise(src, means, sigma),通過次函式生成均值為 means,標準差為 sigma的高斯白噪聲。
椒鹽噪聲又稱脈衝噪聲,它是一種隨機出現的白點或者黑點。椒鹽噪聲=椒噪聲+鹽噪聲,椒鹽噪聲的值為0(黑色)或者255(白色),這裡假設為等概率的出現0或者255。
下面直接上程式碼:
import random
import cv2
from numpy import random
def GaussianNoise(src, means, sigma, percetage):
NoiseImg = src
NoiseNum = int(percetage * src.shape[0] * src.shape[1])
for i in range(NoiseNum):
randX = random.randint(0, src.shape[0] - 1)
randY = random.randint(0, src.shape[1] - 1)
# NoiseImg[randX, randY] = NoiseImg[randX, randY] + random.gauss(means, sigma)
NoiseImg[randX, randY] = NoiseImg[randX, randY] + random.normal(means, sigma)
if NoiseImg[randX, randY] < 0:
NoiseImg[randX, randY] = 0
elif NoiseImg[randX, randY] > 255:
NoiseImg[randX, randY] = 255
return NoiseImg
def PepperandSalt(src, percetage):
NoiseImg = src
NoiseNum = int(percetage * src.shape[0] * src.shape[1])
for i in range(NoiseNum):
#椒鹽噪聲圖片邊緣不處理,故-1
randX = random.random_integers(0, src.shape[0] - 1)
randY = random.random_integers(0, src.shape[1] - 1)
if random.random_integers(0, 1) <= 0.5:
NoiseImg[randX, randY] = 0
else:
NoiseImg[randX, randY] = 255
return NoiseImg
def imageSumPepperandSalt(origin_path, save_path):
img = cv2.imread(origin_path, 0)
img1 = PepperandSalt(img, 0.2)
cv2.imwrite(save_path, img1)
cv2.imshow('PepperandSalt', img1)
cv2.waitKey(0)
cv2.destroyAllWindows()
def imageSumGaussianNoise(origin_path, save_path):
img = cv2.imread(origin_path, 0)
img1 = GaussianNoise(img, 2, 4, 0.8)
cv2.imwrite(save_path, img1)
cv2.imshow('GaussianNoise', img1)
cv2.waitKey(0)
cv2.destroyAllWindows()
def origin_show(origin_path):
img = cv2.imread(origin_path, )
# 灰度化
# img = cv2.imread(origin_path, 0)
cv2.imshow('origin', img)
cv2.waitKey(0)
cv2.destroyAllWindows()
if __name__ == '__main__':
origin_path = 'butterfly.jpg'
save_path1 = 'butterfly_Gaussian.jpg'
save_path2 = 'butterfly_Salt.jpg'
origin_show(origin_path)
imageSumGaussianNoise(origin_path, save_path1)
imageSumPepperandSalt(origin_path, save_path2)
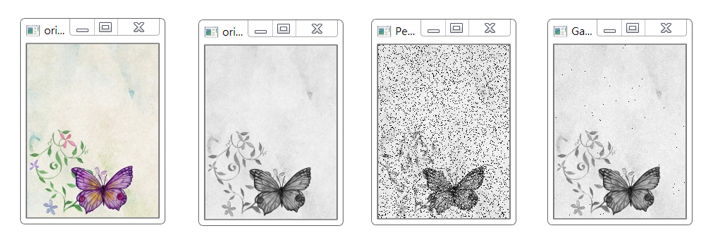
檢視效果:
從左到右依次是 原圖,灰度化圖片,椒鹽噪聲圖片,高斯噪聲圖片
參考文獻:
那張總結圖的來源:https://blog.csdn.net/xv1356027897/article/details/80099027
https://blog.csdn.net/nima1994/article/details/79776802
中值均值:https://blog.csdn.net/qinghuaci666/article/details/81737624
高斯濾波原始碼實現:https://blog.csdn.net/Skymelu/article/details/89086888
均值漂移原理:
https://blog.csdn.net/dcrmg/article/details/52705087
https://blog.csdn.net/qq_23968185/article/details/51804574
https://blog.csdn.net/jinshengtao/article/details/30258833
使用者自定義模糊,均值模糊,中值模糊:https://www.cnblogs.com/FHC1994/p/9097231.html
方框濾波:https://blog.csdn.net/Eastmount/article/details/82216380
https://blog.csdn.net/kaikai______/article/details/5353
