這裡是《神經網路與機器學習》第三章的筆記…
最小均方演算法，即Least-Mean-Square，LMS。其提出受到感知機的啟發，用的跟感知機一樣的線性組合器。
在意義上一方面LMS曾被用在了濾波器上，另一方面對於LMS的各種最優化方式為反向傳播演算法提供了思想基礎。

於是這章書主要是簡單介紹LMS演算法的原理，並介紹幾個簡單的最優化方法，然後用物理熱力學原理描述LMS演算法的學習過程（這個部分太過高深只好跳過）

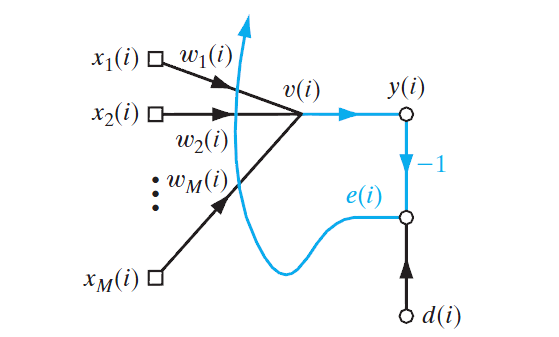
LMS濾波結構

原理上跟感知機也差不多，也是對包含一組共M個元素的x1,x2,...,xM的輸入用一個線性組合器處理，也就是對其進行加權求和，得出結果y，與期望響應d相比較，獲得誤差訊號e

，並由此修正權值，如下圖：

這裡比感知機還要簡單的，直接將區域性誘導域v作為輸出y。因此可以表述成：

y(i)=w1(i)x1(i)+w2(i)x2(i)+...+wM(i)xM(i)=∑k=1Mwk(i)xk(i)

或者寫成向量的形式：

y(i)=x(i)Tw(i)
w(i)即權值向量[w1(i),w2(i),...,wM(i)]T，i表示迭代次數。
誤差訊號為期望響應跟輸出的差，即：e(i)=d(i)−y(i)

無約束最優化問題

LMS演算法的目標就是找到一組權值向量，使其輸出響應跟期望響應最接近。

設立一個代價函式E(w)，其對權值向量連續可微，用來描述輸出響應跟期望響應的差距，也就是值越小越好。於是我們的目標就是醬紫：
找到一個最優的權值向量w

∗，對於任何w都有：

E(w∗)≤E(w)
這是一個無約束最優化問題。其解決的一個必要條件就是∇E(w)=0。
也就是：[∂E∂w1,∂E∂w2,...,∂E∂wM]T=0

一般的解決方法是從一個初始權值向量w(0)開始，不斷迭代產生新的權值向量w(i)，對於每一個權值向量其代價函式都要小於上一個的代價函式，即E(w(i))<E(w(i−1))，如此往復直到代價函式足夠小為止。或者說在一個M維的空間裡，從一個點出發，不停地往代價函式減小的方向走，直到走到最低點。

最速下降法

也就是反向傳播演算法梯度下降的基本原理，在每一個位置w(i)求出當前位置的代價函式的梯度g(i)，再沿著梯度的反方向（正方向使代價函式增加）移動一段距離成為w

(i+1)，也就是每次都順著坡最陡的方向往下走一步。
梯度即為代價函式對權值向量的每一個元素求偏導：

g=∇E(w)=∂E∂w
權值向量的修正為：w(i+1)=w(i)−ηg(i)
η為一個標量，稱為步長或學習率引數，可以理解為沿著梯度方向走的一步的大小。

理論上來說學習率引數η在足夠小的時候，才能完全保證權值向量的修正是讓代價函式一步比一步小的。但是η太小又會導致收斂速度過慢。

定義代價函式：

E(w)=12∑i=1N(di−yi)2=12∑i=1N(di−wTxi)2
那麼就有：g=∂(12∑i=1

相關推薦

記一下機器學習筆記 最小均方（LMS）演算法

這裡是《神經網路與機器學習》第三章的筆記… 最小均方演算法，即Least-Mean-Square，LMS。其提出受到感知機的啟發，用的跟感知機一樣的線性組合器。 在意義上一方面LMS曾被用在了濾波器上，另一方面對於LMS的各種最優化方式為反向傳播演算法提供了

記一下機器學習筆記 多層感知機的反向傳播演算法

《神經網路與機器學習》第4章前半段筆記以及其他地方看到的東西的混雜…第2、3章的內容比較古老預算先跳過。 不得不說幸虧反向傳播的部分是《神機》裡邊人話比較多的部分，看的時候沒有消化不良。 多層感知機 書裡前三章的模型的侷限都很明顯，對於非線性可分問

Python機器學習筆記：線性判別分析（LDA）演算法

預備知識 　　首先學習兩個概念： 　　線性分類：指存在一個線性方程可以把待分類資料分開，或者說用一個超平面能將正負樣本區分開，表示式為y=wx，這裡先說一下超平面，對於二維的情況，可以理解為一條直線，如一次函式。它的分類演算法是基於一個線性的預測函式，決策的邊界是平的，比如直線和平面。一般的方法有感知器，最小

Python機器學習筆記：奇異值分解（SVD）演算法

完整程式碼及其資料，請移步小編的GitHub 　　傳送門：請點選我 　　如果點選有誤：https://github.com/LeBron-Jian/MachineLearningNote 　　奇異值分解（Singular  Value Decomposition，後面簡稱 SVD）是線上性代數中一種

機器學習筆記----最小二乘法，區域性加權，嶺迴歸講解

https://www.cnblogs.com/xiaohuahua108/p/5956254.html 前情提要：關於logistic regression，其實本來這章我是不想說的，但是剛看到嶺迴歸了，我感覺還是有必要來說一下。 一:最小二乘法 最小二乘法的基本思想：基於均方誤差最小化來

記一下機器學習筆記 Rosenblatt感知機

一入ML深似海啊… 這裡主要是《神經網路與機器學習》（Neural Networks and Learning Machines，以下簡稱《神機》）的筆記，以及一些周志華的《機器學習》的內容，可能夾雜有自己的吐槽，以及自己用R語言隨便擼的實現。 話說這個《神

機器學習筆記10-梯度提升樹（GBDT）

機器學習筆記10-梯度提升樹（GBDT） 在上一節中講到了整合學習的Boosting方法，並詳細解釋了其中的代表性演算法AdaBoost演算法。除了AdaBoost演算法外，Boosting中還有另一個非常常用的演算法：提升樹和梯度提升樹（GBDT）。 提升樹 提升樹是以分

機器學習筆記——基於奇異值分解（SVD）的影象壓縮（PIL）

此指令碼的作用是圖片壓縮（清晰度尚可的情況下，可達到8倍以上的壓縮比），是SVD的一個應用實踐，涉及PIL、numpy庫。 （python中處理圖片的庫比較多，比如PIL、OpenCV、matplot

機器學習筆記——最鄰近演算法（KNN）補充

最鄰近演算法補充(K-Nearest Neighbor,KNN) 1、訓練資料集？測試資料集？ 我們在使用機器學習演算法訓練好模型以後，是否直接投入真實環境中使用呢？其實並不是這樣的，在訓練好模型後我們往往需要對我們所建立的模型做一個評估來判斷當前機器學習演算法的效能，當我們在

【機器學習】最小二乘法求解線性迴歸引數

回顧 迴歸分析之線性迴歸 中我們得到了線性迴歸的損失函式為： J ( θ

【機器學習】最小二乘法支援向量機LSSVM的數學原理與Python實現

【機器學習】最小二乘法支援向量機LSSVM的數學原理與Python實現 一、LSSVM數學原理 1. 感知機 2. SVM 3. LSSVM 4. LSSVM與SVM的區別 二、LSSVM的py

[學習筆記]最小割之最小點權覆蓋&&最大點權獨立集

最小點權覆蓋 給出一個二分圖，每個點有一個非負點權要求選出一些點構成一個覆蓋，問點權最小是多少   建模： S到左部點，容量為點權 右部點到T，容量為點權 左部點到右部點的邊，容量inf 求最小割即可。   證明： 每一個割集，對應選擇一些點，對應一個覆蓋。 每個覆蓋

學習筆記--最小圓覆蓋

隨機化各點後暴力列舉，發現三點定的圓不能包含當前點就更新。。複雜度期望O（n）（不會證。。） 模板題：bzoj1336 #include<bits/stdc++.h> #define db double using namespace std; const i

[學習筆記]最小割樹

用於求任意兩個點的最小割（最大流） Gomory-Hu tree (最小割樹) 介紹及實現 - jyxjyx27的專..._CSDN部落格 最小割樹建造方法： 類似於分治 在當前點集中選擇任意兩個點作為源點、匯點，跑最小割G 兩個點之間連樹邊，邊權為G 把當前點集中和源點聯

機器學習_最小二乘法，線性迴歸與邏輯迴歸

1. 線性迴歸  線性迴歸是利用數理統計中迴歸分析，來確定兩種或兩種以上變數間相互依賴的定量關係的一種統計分析方法。  直觀地說，在二維情況下，已知一些點的X,Y座標，統計條件X與結果Y的關係，畫一條直線，讓直線離所有點都儘量地近（距離之和最小），用直線抽象地表達這些點，然後對新的X預測新的Ｙ。具體實現一般

機器學習之最小二乘法：背後的假設和原理

1 最小二乘法相關理論 我們先從最基本但很典型的線性迴歸演算法之最小二乘法說起吧，它背後的假設和原理您瞭解嗎？本系列帶來細細體會OLS這個演算法涉及的相關理論和演算法。 參考推送： 似然函式求權重引數 似然函式的確是求解類似問題的常用解決方法，包

[學習筆記]最小樹形圖——朱劉演算法

處理這樣一類問題： 給一個有向圖，定義樹形圖：一個有向圖以x為根的樹形圖，是一個n-1條邊的集合，使得x能到達其他每一個點 樹形圖的權值定義為邊的和 朱劉演算法就是求最小樹形圖   方法： 1.給每個點p找一個邊權最小的連向它的邊，邊權為val，前驅設為pre。找到了一個邊集E0 an

哈工大《機器學習》最小二乘法曲線擬合——實驗一

程式碼更多細節待更新。 目標： 掌握最小二乘法求解（無懲罰項的損失函式）、掌握加懲罰項（2範數）的損失函式優化、梯度下降法、共軛梯度法、理解過擬合、克服過擬合的方法(如加懲罰項、增加樣本) 已完成的要求： 生成資料，加入噪聲； 用高階多項式函式擬合曲線； 用解

機器學習的最小可用產品：人工智慧應用的敏捷開發

我們曾經在公眾號上發過一篇文章《年薪百萬的機器學習專家，為什麼不產生價值？》，文中的機器學習專家花了大量的時間搭建平臺，做資料的清洗、處理與機器學習建模，卻沒有帶來公司所期望的價值。問題出在哪裡了呢？ 基於第四正規化在機器學習工業應用方面的大量成功案例和經驗，我們今天就來

機器學習中最小二乘和梯度下降法的個人理解

提前說明一下，這裡不涉及數學公式的推到，只是根據自己的理解來概括一下，有不準確的地方，歡迎指出。最小二乘：我們通常是根據一些離散的點來擬合出一天直線，這條直線也就是我們所說的模型，最小二乘也就是評價損失函式（loss）的一個指標。最小二乘就是那些離散的點與模型上擬合出的點做一