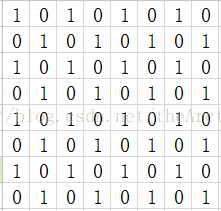棋盤的完美覆蓋(多米諾骨牌完美覆蓋)&&幻方(魔方陣)
棋盤的完美覆蓋:
一張8行8列的棋盤一共有64個方格,用一些形狀相同的多米諾骨牌覆蓋,每一張覆蓋相鄰的兩個方格,沒有相互重疊,能用32張這樣的多米諾骨牌完全覆蓋整張棋盤稱為多米諾骨牌完美覆蓋或者蓋瓦。這樣的完美覆蓋是存在的,而且不止一種方式,一共有12988816=2^4*17^2*53^2種。那麼對於一般的m行n列的棋盤是否存在著多米諾骨牌完美覆蓋呢?充要條件是m*n是偶數,這等價於分子物理學中的二聚物問題。有這樣的問題:如果把8行8列的棋盤的一條對角線上的兩個角的方格去掉,那麼完美覆蓋還有多少種呢?這樣分析:每一張骨牌覆蓋相鄰的兩個方格,那麼就假設棋盤是黑白相間的,呈現這樣的場景(1代表黑,0代表白):
去掉的兩個方格必然是相同的顏色,於是原來32張黑色和32張白色變成了30黑色(白色),32白色(黑色)。如果31張骨諾牌能夠完美覆蓋,那麼就產生了這樣的關係式:31(black+white)=30black+32white [or: 30white+32black] 這顯然是不成立的。所以一種完美覆蓋都不存在。
拓展:如果棋盤的規格是m*n,且一張牌的長度是b(稱作b格牌),那麼這樣的棋盤能夠被b格牌完美覆蓋嗎?顯然,想要完美覆蓋,b必然是m*n的因子,這就是充分條件:b是m或者n的因子(聯絡實際)。事實上有這樣的結論:m*n的棋盤有b格牌的完美覆蓋當且僅當b是m或者n的一個因子。
幻方:
一個由數字1,2,3--n^2組成n行n列的n階的幻方,滿足每一行每一列兩條對角線上的數字之和是等值的,假設這樣的值是s。那麼有這樣的等式:n*s=1+2+3+--+n^2=(n^2+1)/2*n^2. -->s=n*(n^2+1)/2. 所以我們可以推斷2階的魔方陣是不存在的,不然s=5啊,顯然這是不可能的。幻方的構造和很多方法,n為奇數時有這樣一種應用較廣的構造方法:首先把1放在第一行的中間,然後按照左下方到右上方的順序擺放各個數字(行數i和列數j的變化趨勢:向量(i-1,j+1)),遇到特殊的情況:
(1)當下一個數字到達已有數字的位置或者四個對角線方向的方陣外時,直接把新的數字放到上一個數字的下面。
(2)當下一個數字的行數到了0時,行數變為n,列數照常加1。
(3)當下一個數字的列數到了n+1時,列數變為1,行數照常減1。
奇數階幻方(16階內):
#include"stdio.h" void xiabiao(int &a, int &b,int n) { a-=1; b+=1; if(a<0 && b>n-1){ a+=2; b-=1; } if(a<0)a=n-1; if(b>n-1)b=0; } main() { int m[16][16],n;/*h表示最中間的列數*/ int i,j,k=1; while(~scanf("%d",&n)&&n) //enter a number n. { if(n%2==0 || n<1 || n>16)continue; for(i=0;i<n;i++) for(j=0;j<n;j++) m[i][j]=1; i=0; j=n/2; k=1; while(k<n*n) { xiabiao(i,j,n); if((m[i][j]<k && m[i][j]!=1) || (i==0 && j==n/2)){ i+=2; j-=1; } m[i][j]=++k; } for(i=0;i<n;i++) { for(j=0;j<n;j++) printf("%5d",m[i][j]); printf("\n"); } } }
當n是偶數時分成4k(雙偶數)和4k+2(單偶數)階討論:對於4k,先說說最簡單的4階情況。先把所有的元素從左到右從上到下順序填寫完整,再把對角線 上的所有元素標記,其他元素按照中心對稱位置關係兩兩互換。即可達到幻方效果。將其推廣,當k=2,3,4……時同樣先順序填寫,再把整個方陣劃分成(n/4)*(n/4)個4階陣,把所有的四階陣兩條對角線的元素標記固定不動,然後再把n*n的方陣的所有非對角線元素以方陣中心為對稱點進行中心對稱互換(那麼對稱點的位置關係就是(x1,y1)+(x2,y2)=(n+1,n+1)),最終即可構成n階幻方陣。
雙偶數階幻方(16階內):
#include"stdio.h"
#include"string.h"
int m[17][17],n;
bool vis[17][17];
void swap(int *a,int *b){
int t=*a;
*a=*b;
*b=t;
}
void show(){
int i,j;
for(i=1;i<=n;i++){
for(j=1;j<=n;j++){
printf("%5d",m[i][j]);
}
printf("\n");
}
}
void block(){
int i,j,k,re=n/4;
for(i=0;i<re;i++){
for(j=0;j<re;j++){
for(k=1;k<=4;k++){
vis[k+4*i][k+4*j]=vis[k+4*i][4+1-k+4*j]=1;
}
}
}
for(i=1;i<=n/2;i++){
for(j=1;j<=n;j++){
if(vis[i][j])continue;
swap(&m[i][j],&m[n+1-i][n+1-j]);
}
}
}
int main(int argc, char *argv[]) {
freopen("cin.txt","r",stdin);
freopen("cout.txt","w",stdout);
int i,j,k;
while(~scanf("%d",&n)&&n){
memset(vis,0,sizeof(vis));
k=1;
for(i=1;i<=n;i++){
for(j=1;j<=n;j++){
m[i][j]=k++;
}
}
//show();
block();
show();
}
return 0;
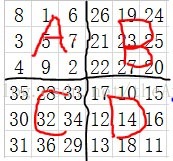
}4k+2階的幻方則稍複雜一點,有這樣的方法:現將方陣劃分成兩個區,邊界上所有元素為一個區A,邊界內的所有元素構成一個區B,B區即是一個4k陣,把8k+3--16k^2+8k+2的數字填入雙偶數陣按照前面的方法進行變化。然後剩下的元素放到邊界進行試調,直到滿足幻方的條件即可。當然這樣在計算機上很難實現。還有一種易於實現的方法:把方陣分為A,B,C,D四個象限,這樣每一個象限肯定是奇數階。依次在A象限,D象限,B象限,C象限按奇數階幻方的填法填數。以6階為例如同:
在A象限的中間行、中間格開始,按自左向右的方向,標出k格。A象限的其它行則標出最左邊的k格。將這些格,和C象限相對位置上的數,互換位置。
在B象限任每行的中間格,自右向左,標出k-1列。(注:6階幻方由於k-1=0,所以不用再作B、D象限的資料交換), 將B象限標出的這些數,和D象限相對位置上的數進行交換,就形成幻方。
單偶數階幻方(16階內):
#include <iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int m[17][17],tag[17][17],n;
int i,j,k;
void show(){
for(i=1;i<=n;i++){
for(j=1;j<=n;j++){
printf("%5d",m[i][j]);
}
printf("\n");
}
}
void inital(){ //(1,1),(1,n/2+1),(1+n/2,1),(1+n/2,1+n/2)
int num;
memset(m,0,sizeof(m));
int lo[4][2]={{0,0},{n/2,n/2},{0,n/2},{n/2,0}};
for(k=0;k<4;k++){
num=1+(n/2)*(n/2)*k;
i=lo[k][0]+1;
j=n/2/2+lo[k][1]+1;
int ik=num;
m[i][j]=ik++;
while(ik<num+(n/2)*(n/2))
{
i-=1;
j+=1;
if(i<lo[k][0]+1&& j>n/2+lo[k][1]){ i+=2; j-=1; }
if(i<lo[k][0]+1)i=n/2+lo[k][0];
if(j>n/2+lo[k][1])j=1+lo[k][1];
if((m[i][j]<ik && m[i][j])){ i+=2; j-=1; }
m[i][j]=ik++;
}
}
}
void write(){
memset(tag,0,sizeof(tag));
j=1+n/2/2;
k=n/4;
while(k--){
tag[n/2/2+1][j++]=1;
}
for(i=1;i<=n/2;i++){
if(i==n/2/2+1)continue;
for(j=1;j<=n/4;j++)tag[i][j]=1;
}
for(i=1;i<=n/2;i++){
j=n/2+n/2/2+1;
k=n/4-1;
while(k--){
tag[i][j--]=1;
}
}
}
void showtag(){
for(i=1;i<=n;i++){
for(j=1;j<=n;j++){
printf("%5d",tag[i][j]);
}
cout<<endl;
}
}
void swap(int &a,int &b){
int t=a;
a=b;
b=t;
}
void change(){
for(i=1;i<=n/2;i++){
for(j=1;j<=n;j++){
if(tag[i][j])swap(m[i][j],m[i+n/2][j]);
}
}
}
int main(int argc, char *argv[]) {
freopen("cin.txt","r",stdin);
freopen("cout.txt","w",stdout);
while(cin>>n&&n){
inital();
write();
//showtag();
change();
show();
}
return 0;
}
/*
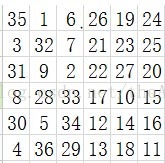
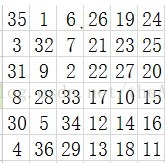
6階:
35 1 6 26 19 24
3 32 7 21 23 25
31 9 2 22 27 20
8 28 33 17 10 15
30 5 34 12 14 16
4 36 29 13 18 11
10階:
92 99 1 8 15 67 74 26 58 65
98 80 7 14 16 73 55 32 64 66
4 6 88 95 22 54 56 38 70 72
85 87 19 21 3 60 62 44 71 53
86 93 25 2 9 61 68 50 52 59
17 24 76 83 90 42 49 51 33 40
23 5 82 89 91 48 30 57 39 41
79 81 13 20 97 29 31 63 45 47
10 12 94 96 78 35 37 69 46 28
11 18 100 77 84 36 43 75 27 34
14階:
177 186 195 1 10 19 28 128 137 97 50 108 117 126
185 194 154 9 18 27 29 136 145 56 58 116 125 127
193 153 155 17 26 35 37 144 104 57 66 124 133 135
5 14 16 172 181 183 45 103 112 65 74 132 134 143
160 162 171 33 42 44 4 111 113 73 82 140 142 102
168 170 179 41 43 3 12 119 121 81 90 141 101 110
169 178 187 49 2 11 20 120 129 89 98 100 109 118
30 39 48 148 157 166 175 79 88 146 99 59 68 77
38 47 7 156 165 174 176 87 96 105 107 67 76 78
46 6 8 164 173 182 184 95 55 106 115 75 84 86
152 161 163 25 34 36 192 54 63 114 123 83 85 94
13 15 24 180 189 191 151 62 64 122 131 91 93 53
21 23 32 188 190 150 159 70 72 130 139 92 52 61
22 31 40 196 149 158 167 71 80 138 147 51 60 69
*/