感謝博主分享
原文地址–寫於 2017-01-12

參考文獻連結

漢語版翻譯如下

Kaggler的“實踐中模型堆疊指南”

介紹
堆疊（也稱為元組合）是用於組合來自多個預測模型的資訊以生成新模型的模型組合技術。通常，堆疊模型（也稱為二級模型）因為它的平滑性和突出每個基本模型在其中執行得最好的能力，並且抹黑其執行不佳的每個基本模型，所以將優於每個單個模型。因此，當基本模型顯著不同時，堆疊是最有效的。關於在實踐中怎樣的堆疊是最常用的，這裡我提供一個簡單的例子和指導。

本教程最初發布在Ben的部落格GormAnalysis上。

另外的python 版本的blending

動機
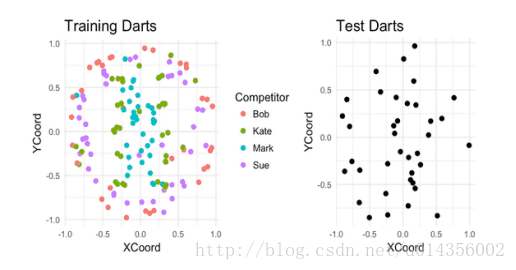
假設有四個人在板子上投了187個飛鏢。對於其中的150個飛鏢，我們可以看到每個是誰投擲的以及飛鏢落在了哪。而其餘的，我們只能看到飛鏢落在了哪裡。我們的任務就基於它們的著陸點來猜測誰投擲的每個未標記的飛鏢。

K最近鄰（基本模型1）
讓我們使用K最近鄰模型來嘗試解決這個分類問題。為了選擇K的最佳值，我們將使用5重交叉驗證結合網格搜尋，其中K =（1,2，… 30）。在虛擬碼中：
1.將訓練資料分成五個大小相等的資料集。呼叫這些交叉測試。
2.對於K = 1,2，… 10
1.對於每個交叉測試
1.組合其他四個交叉用作訓練交叉
2.在訓練交叉上使用K最近鄰模型（使用K的當前值）
3.對交叉測試進行預測，並測量所得預測的準確率
2.從五個交叉測試預測中計算平均準確率
3.保持K值具有最好的平均CV準確率
使用我們的虛構資料，我們發現K = 1具有最佳的CV效能（67％的準確性）。使用K = 1，我們現在訓練整個訓練資料集的模型，並對測試資料集進行預測。 最終，這將給我們約70％的分類精度。

支援向量機（基本型2）
現在讓我們再次使用支援向量機解決這個問題。此外，我們將新增一個DistFromCenter功能，用於測量每個點距板中心的距離，以幫助使資料線性可分。 使用R的LiblineaR包，我們得到兩個超引數來調優：
型別
1.L2-正則化L2丟失支援向量分類（雙重）
2.L2正則化L2丟失支援向量分類（原始）
3.L2-正則化L1損失支援向量分類（雙重）
4.Crammer和Singer的支援向量分類
5.L1正則化L2丟失支援向量分類
成本
正則化常數的倒數
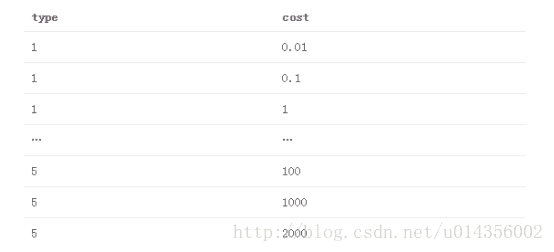
我們將測試的引數組合網格是5個列出的SVM型別的笛卡爾乘積，成本值為（.01，.1，10，100，1000，2000）。 那是

使用與我們的K最近鄰模型相同的CV +網格搜尋方法，這裡我們找到最好的超引數為type = 4，cost = 1000。再次，我們使用這些引數訓練的模型，並對測試資料集進行預測。這將在測試資料集上給我們約61％的CV分類精度和78％的分類準確性。

堆疊（元組合）

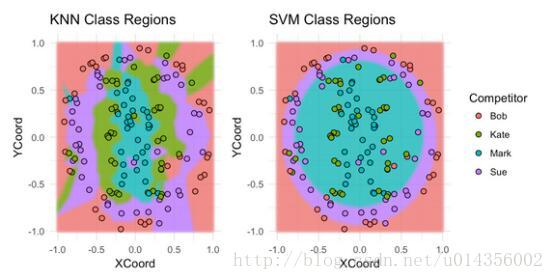
讓我們來看看每個模型分為Bob，Sue，Mark或Kate的板區域。

不出所料，SVM在分類Bob的投擲和Sue的投擲方面做得很好，但是在分類Kate的投擲和Mark的投擲方面做得不好。對於最近鄰模型，情況正好相反。 提示：堆疊這些模型可能會卓有成效。
一共有幾個思考如何實現堆疊的派別。在我們的示例問題中我是根據自己的喜好來應用的：
1.將訓練資料分成五個交叉測試

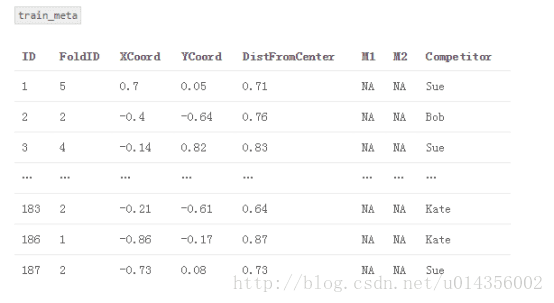
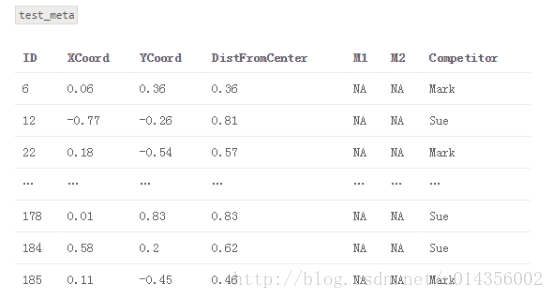
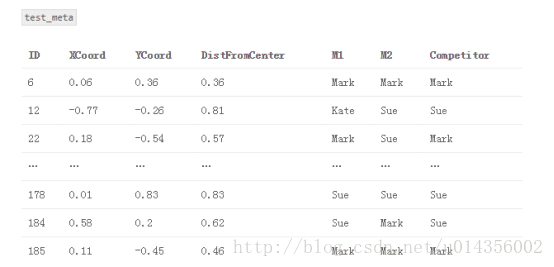
2.建立一個名為“train_meta”的資料集，其具有與訓練資料集相同的行ID和交叉ID、空列M1和M2。 類似地，建立一個名為“test_meta”的資料集，其具有與測試資料集相同的行ID、空列M1和M2

3.對於每個交叉測試
{Fold1，Fold2，… Fold5}
3.1組合其他四個交叉用作訓練交叉

3.2對於每個基本模型
M1：K-最近鄰（k = 1）
M2：支援向量機（type = 4，cost = 1000）
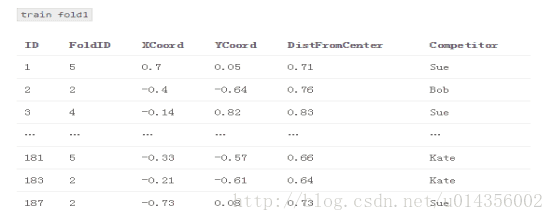
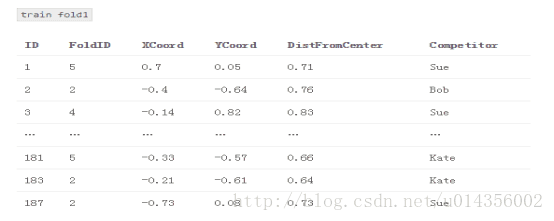
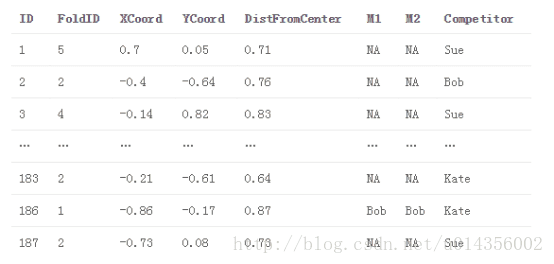
3.2.1將基本模型交叉訓練，並在交叉測試進行預測。 將這些預測儲存在train_meta中以用作堆疊模型的特徵
train_meta與M1和M2填補fold1

4.將每個基本模型擬合到完整訓練資料集，並對測試資料集進行預測。 將這些預測儲存在test_meta內

5.使用M1和M2作為特徵，將新模型S（即，堆疊模型）適配到train_meta，可選地，包括來自原始訓練資料集或特徵工程的其他特徵。
S：邏輯迴歸（來自LiblineaR包，型別= 6，成本= 100）。 適配train_meta
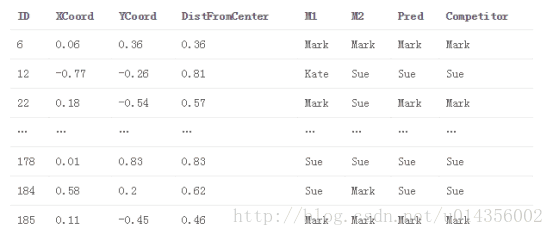
6.使用堆疊模型S對test_meta進行最終預測
test_meta與堆疊模型預測

主要觀點是，我們使用基礎模型的預測作為堆疊模型的特徵（即元特徵）。 因此，堆疊模型能夠辨別哪個模型表現良好，哪個模型表現不佳。還要注意的是，train_meta的行i中的元特徵不依賴於行i中的目標值，因為它們是在使用基本模型擬合過程中排除target_i的資訊中產生的。
或者，我們可以在測試資料集適合每個交叉測試之後立即使用每個基本模型進行預測。 在我們的例子中，這將產生五個K-最近鄰模型和五個SVM模型的測試集預測。然後，我們將平均每個模型的預測以生成我們的M1和M2元特徵。 這樣做的一個好處是，它比第一種方法耗時少（因為我們不必在整個訓練資料集上重新訓練每個模型）。 它也有助於我們的訓練元特徵和測試元特徵遵循類似的分佈。然而，測試元M1和M2在第一種方法中可能更準確，因為每個基礎模型在全訓練資料集上訓練（相對於訓練資料集的80％，在第二方法中為5次）。
堆疊模型超引數調優
那麼，如何調整堆疊模型的超引數？ 關於基本模型，就像我們以前做的，我們可以使用交叉驗證+網格搜尋調整他們的超引數。 我們使用什麼交叉並不重要，但使用我們用於堆疊的相同交叉通常很方便。調整堆疊模型的超引數是讓事情變得有趣的地方。在實踐中，大多數人（包括我自己）只需使用交叉驗證+網格搜尋，使用相同的精確CV交叉用於生成元特徵。 這種方法有一個微妙的缺陷 - 你能找到它嗎？
事實上，在我們的堆疊CV過程中有一點點資料洩漏。 想想堆疊模型的第一輪交叉驗證。我們將模型S擬合為{fold2，fold3，fold4，fold5}，對fold1進行預測並評估效果。但是{fold2，fold3，fold4，fold5}中的元功能取決於fold1中的目標值。因此，我們試圖預測的目標值本身就嵌入到我們用來擬合我們模型的特徵中。這是洩漏，在理論上S可以從元特徵推匯出關於目標值的資訊，其方式將使其過擬合訓練資料，而不能很好地推廣到袋外樣本。 然而，你必須努力工作來想出一個這種洩漏足夠大、導致堆疊模型過度擬合的例子。 在實踐中，每個人都忽略了這個理論上的漏洞（坦白地說，我認為大多數人不知道它甚至存在！）
堆疊模型選擇和特性
你如何知道選擇何種型號作為堆疊器以及元特徵要包括哪些功能？ 在我看來，這更像是一門藝術而不是一門科學。 你最好的辦法是嘗試不同的東西，熟悉什麼是有效的，什麼不是。另一個問題是，除了元特徵，你應該為堆疊模型包括什麼其他功能（如果有）？這也是一種藝術。看看我們的例子，很明顯，DistFromCenter在確定哪個模型將會很好地發揮作用。KNN似乎在分類投擲於中心附近的飛鏢上做得更好，SVM模型在分類遠離中心的飛鏢上表現得更好。 讓我們來看看使用邏輯迴歸來堆疊我們的模型。 我們將使用基本模型預測作為元特徵，並使用DistFromCenter作為附加功能。
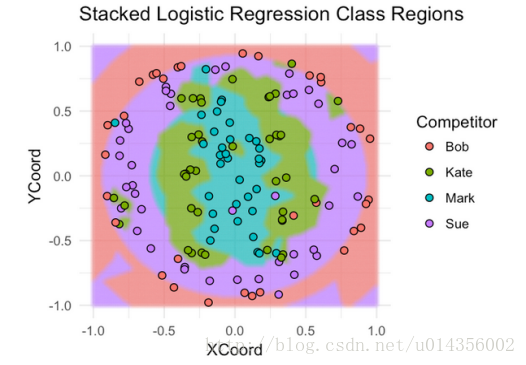
果然，堆疊模型的效能優於兩種基本模型 - 75％CV精度和86％測試精度。 就像我們對基本模型一樣，現在讓我們來看看它的覆蓋訓練資料的分類區域。

這裡的好處是，邏輯迴歸堆疊模型捕獲每個基本模型的最好的方面，這就是為什麼它的執行優於任何孤立的基本模型。
實踐中的堆疊
為了包裝，讓我們來談談如何、何時、以及為什麼在現實世界中使用堆疊。 就個人而言，我大多在Kaggle的機器學習競賽中使用堆疊。一般來說，堆疊產生小的收益與大量增加的複雜性不值得為大多數企業使用。 但堆疊幾乎總是富有成果，所以它幾乎總是用於頂部Kaggle解決方案。 事實上，當你有一隊人試圖在一個模型上合作時，堆疊對Kaggle真的很有效。採用一組單獨的交叉，然後每個團隊成員使用那些交叉建立他們自己的模型。 然後每個模型可以使用單個堆疊指令碼組合。這是極好的，因為它防止團隊成員踩在彼此的腳趾，尷尬地試圖將他們的想法拼接到相同的程式碼庫。
最後一位。 假設我們有具有（使用者，產品）對的資料集，並且我們想要預測使用者在購買給定產品的情況下，他/她與該產品一起展示廣告的機率。一個有效的功能可能是，使用培訓資料，有多少百分比的產品廣告給使用者，而他實際上在過去就已經購買？因此，對於訓練資料中的樣本（user1，productA），我們要解決一個像UserPurchasePercentage這樣的功能，但是我們必須小心，不要在資料中引入洩漏。 我們按照接下來這樣做：
1.將訓練資料拆分成交叉
2.對於每個交叉測試
1.標識交叉測試中的唯一一組使用者
2.使用剩餘的交叉計算UserPurchasePercentage（每個使用者購買的廣告產品的百分比）
3.通過（fold id，使用者id）將UserPurchasePercentage映射回培訓資料
現在我們可以使用UserPurchasePercentage作為我們的梯度提升模型（或任何我們想要的模型）的一個特性。我們剛剛做的是有效地建立一個預測模型，基於user_i在過去購買的廣告產品的百分比，預測他將購買product_x的概率，並使用這些預測作為我們的真實模型的元特徵。這是一個微妙而有效並且我經常在實踐和Kaggle實現的有效的堆疊形式 - 。