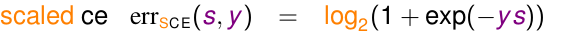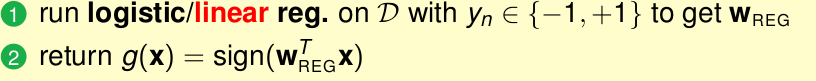將 線性迴歸 ，logistic 迴歸 用在 分類 上面

我們回顧一下上節所學習的內容。總共學習了三種線性模型（線性分類，線性迴歸，logistic 迴歸）,他們的核心都是
他們三種情況分別為

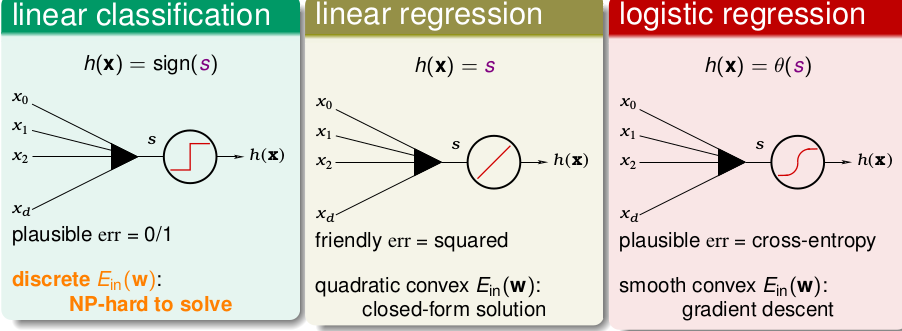
那麼問題是，能否將線性迴歸，logistic 迴歸 運用到 線性分類 呢？？
其實，分類是一種特殊的迴歸，只是輸出的結果y僅僅為{-1,1}罷了！
分類問題，對於某一個樣本，其y僅為-1或者1。該樣本的誤差為err(s,y) 。注意：不是Ein，err(s,y)表示某一個樣本的誤差，而Ein表示的是將所有樣本的err(s,y)相加的和再除以N，得到的平均值。
那麼三種模型的err(s,y)分別為

注意：由於是分類問題，那麼上圖的y只能為1或者-1。但是s的值就不是僅僅只有1或者-1了。
那求得的三種模型的err(s,y)就分別為

0/1表示 線性分類的。 sqr表示線性迴歸的。ce表示logistic迴歸的。
以ys為橫座標，err值為縱座標。則可匯出圖形為

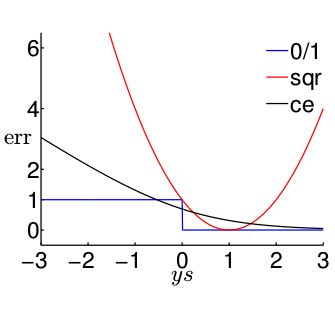
我們來看看ys的物理意義。y是樣本的標籤，s是模型對這個樣本預測的值,s=wTx為實數,無窮多個取值。如果y=1，那麼我們肯定希望s>0，如果y=-1，那麼我們肯定希望s<0。所以，ys>0表示 模型分類正確，ys<0表示模型分類錯誤。
1. 我們來看看0/1模型的情況，ys>0,err=0；ys<0,err=1.
2. 但是，我們看sqr模型就不一樣了。ys<<1,err很大，(哎，大就大唄，反正ys<0，是應該受點懲罰，只是這懲罰有點大)。但是當ys>>1，時，為什麼sqr模型的err卻依然那麼大啊！！！ys>>1,表示的是模型分類是正確，err為0 才對，為什麼還越來越大。所以，只有使得sqr的err很小時，此時的sqr才會和0/1的err相接近，才會一樣小。所以我們是sqr的err小的話，可以使得0/1的err也小；但是0/1的err小，並不代表sqr的err小。
3. 再看ce模型。很顯然，ce的err小的話，0/1的err也小；0/1的err小的話（不管怎麼小，都為0），ce 也小。
為了方便，我們對ce err的表示式除了l

得到圖形為

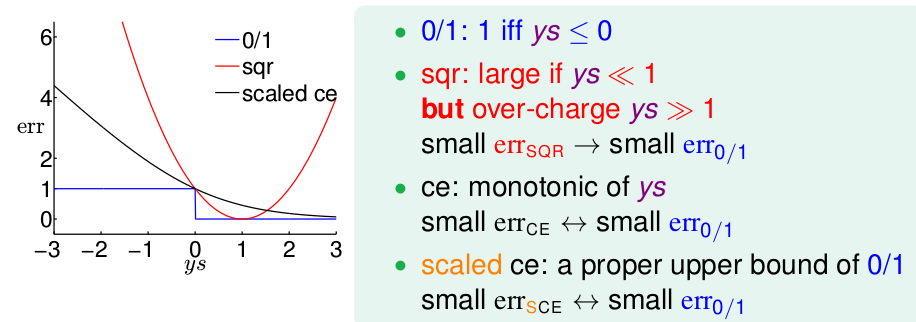
這樣曲線恆再0/1曲線的上方。err是一個樣本的誤差,Ein是把所有的err求和去平均就有

對0/1和ce模型分別用之前討論的VC bound Eout<=Ein+...‾‾‾√
即
即可知，只要我們保證 ce Ein足夠小，就可以保證0/1分類的 Ein小。同理 只要我們保證 linear regression Ein足夠小，就可以保證0/1分類的 Ein小。
所以可以將線性迴歸和邏輯迴歸用再分類上面。
方法就是，我們用線性迴歸或邏輯迴歸用分類的樣本（y={-1，1}）求出權重w,再得到sign(wx)即可.
即

隨機梯度法 SGD

我們回顧以前講的內容，發現 總共學習了兩種迭代優化的方法–PLA和logistic 迴歸
這兩種方法的核心為

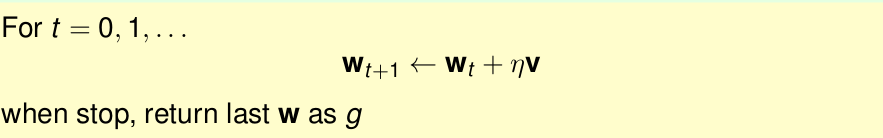
PLA的思想是，每次迭代我只取出一個樣本，進行處理。即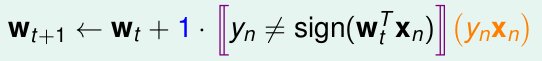，那麼他每次迭代的複雜度僅僅只有O(1) time。
而logistic 迴歸的思想是，每次迭代取出所有的樣本來求出梯度值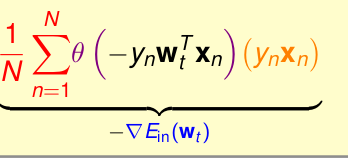。那麼他的複雜度為O(N) time。
所以，我們能否也讓logisitc 迴歸每次迭代的複雜度為O(1)呢？
我們以前用logistic迴歸的公式為

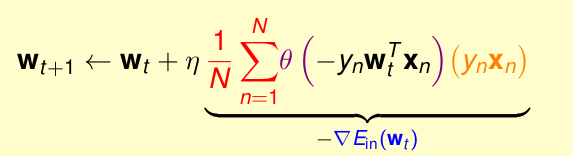
這是我們用梯度下降法得到的，他的Ein是沿著梯度的方向向下走的。那麼為了能讓複雜度為O(1)，我們不強求下降方向一定要是梯度，也就是大概梯度方向就行。即
發現公式裡是“約等號”，以前的方法是等號。
那怎樣做到這一點呢？？？

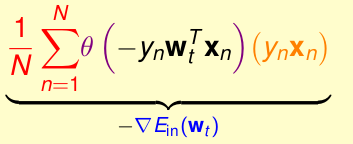
其實我們可以把上圖看成是，期望值（也就是均值）。你有10000個數字，求他們的期望，由於太複雜，我就隨機抽取幾個點去求這幾個點的期望。這就好比我們現在的隨機梯度法，只是隨機梯度法隨機僅僅抽取的1個點，求這一個點的期望（就是他本身）。我們就用這一個點的期望去替代總體樣本的期望。這就把原始的梯度下降法改成了我們現在的隨機梯度法。
所以運用隨機梯度法替代原來的梯度下降法，最終得到的公式為

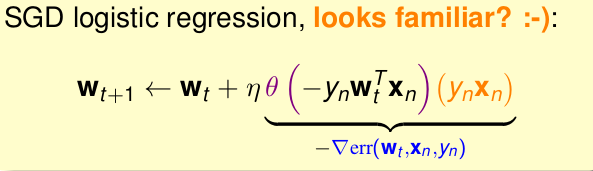
優點：快，運輸量低，適於大資料，適於線上學習online learning
缺點：穩定性會降低，
由於無法達到最低，所以停止條件是：迴圈足夠多次
一般取η為0.1（個人習慣，和個人經驗）

SGD logistic迴歸與PLA的關係

用logistic迴歸做多分類問題

現在我們想分類成為下圖的樣本進行分類

方法一：
我們用二分類的分類器幫助我們進行多分類

思想：我們每次抽取一個類別比如“方塊”，將其作為“o”，其他的所有的類別作為“×”，依次這樣，我們可以做出4個分類器。

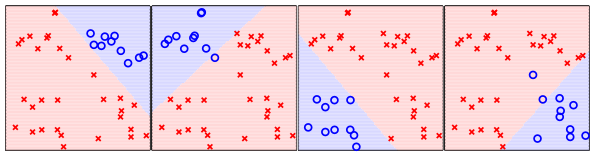
以上4個分類器依次對方塊，菱形，三角，五角星 分類。
現在，我有一個新樣本，他位於方框的右上角。很顯然，第一個分類器說是“o”,而其他的分類器幾乎都說是”×”，那麼我們就可以說這個新樣本的類別就是“方框”。也就是說，以後來的新樣本，一般（僅一般情況）有一個分類器說是“o”，其他三個說是“×”。那麼就可以說這個樣本屬於這個說“o”的分類器對應的標籤 了。
但是存在一個很大的問題

就是在上圖中的正中心，每個分類器都會說是“×”，在正中心的正上，正下，正左，正右，四個小塊都會有兩個分類器說是“o”。
所以，這種用二分類，結果僅能是“×”或者“o”的方法，存在不可解的情況。
那麼我們就不那麼絕對，一定要是“×”或者“o”。我們用概率的形式來做。
現在就來介紹，這一部分的主人公：
多分類之logistic迴歸 OVA(1對多 one versus all)
該方法與上面的思路基本相同。也是對每個類別和其他所有的類做分類器，所以也是做4個分類器。不同之處是，每一個小 分類器的輸出，不在是絕對的“o”或者“×”，而是屬於“o”的概率。假如我有一個樣本，把他帶入4個分類器，計算出該樣本在每一個分類器上面屬於“o”的概率值，取出概率值最大的那個分類器，該分類器對應的類別就是新樣本的類別。

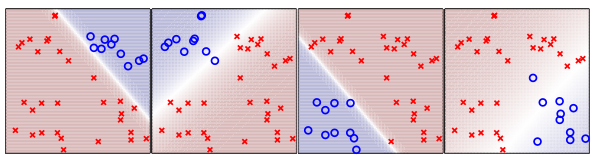
上面四個分類器，把新樣本帶入4個分類器，計算出該樣本在每一個分類器上面屬於“o”的概率值，取出概率值最大的那個分類器，該分類器對應的類別就是新樣本的類別。
即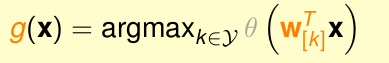
演算法總結為：
1. 對於k個類別，迴圈k次
第i次，取出第i個類作為“o”，其他所有類（k-1個)都作為“×”，用logistic 迴歸訓練概率模型（輸出結果為 屬於“o”的概率）
迴圈k次，則有k個logistic模型
2. 把新樣本依次帶入k個分類器，計算出該樣本在每一個分類器上面的輸出（屬於“o”的概率值），輸出值（屬於”o”概率值）最大的那個分類器對應的類別就是新樣本的類別。
即
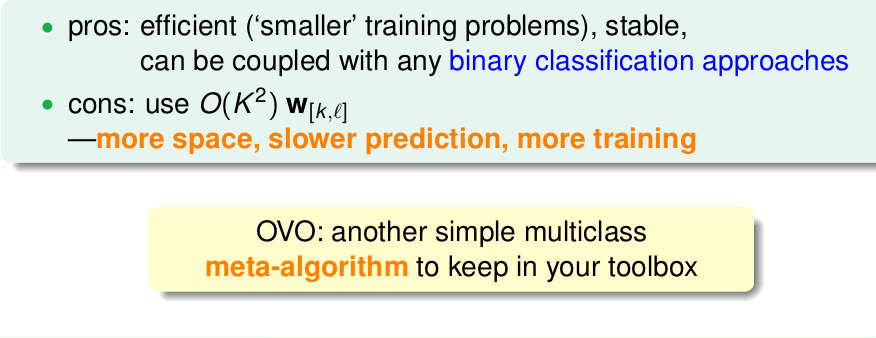
優點：效率高，用的是logistic迴歸
缺點：當k很大，每個類對應的樣本數相對於N就會很小，那麼就會很不穩定。原因：見下：（但這依然是個很好的方法，在k不大的情況下）
一對多有個問題
當你的類別k很大的時候，即每個類別樣本的數量相對於N都很小，那麼每個類別的分類器都會努力的去猜‘×’。假如N=100，你的類別K=100，那麼對於每一個類別分類器，都是，僅有一個樣本為“o”,其他99個都是”×”。也就是說模型都會去猜“×”，那麼每個小模型都有99%的正確率。那麼你的最終模型就是在一堆都愛猜“×”的模型裡選一個最大的類別。很顯然，這樣結果就會不穩定，並不是很好，並且你還會以為很好。

用線性分類投票法做多分類問題 （1對1 ）（one versus one)

上面的演算法是對於K個類別，每次選取1個類別作為“o”，其他所有的類別作為“×”，所以叫 1對多（one versus all）。總共迴圈k次。
而這次這個演算法，每次選取1個作為“o”，再選一個類別作為“×”，用這兩個類的資料訓練小模型，所以稱為 1對1（one versus one）。總共迴圈C2k次。共C2k個模型。
比如有4個類，k=4，那麼總共有C24=6個模型，如下圖


假設有一個新樣本，假設他位於右上角，我們把他依次放在這6個模型中。那麼第一個模型輸出結果為“方塊”，第二個模型輸出結果為“方塊”，第三個模型輸出結果為“方塊”，第四個模型輸出結果為“菱形”，第五個模型輸出結果為“五角星”，第六個模型輸出結果為“五角星”。那麼經過投票，得到最終這個新樣本的類別為“方塊”。
演算法總結：
1. 有k個類別，那麼我們迴圈C2k次
對於第i次迴圈，取出一個類別資料作為“o”，再取出一個類別資料作為“×”，用linear classfication 訓練小模型。
所以總共有C2k次
2. 把新樣本依次投入C2k個小模型裡，運用投票的方法，選出k個類別中獲得票數最佳的類別作為新樣本的類標籤。

優缺點：