問題的引入：

考慮一個典型的有監督機器學習問題，給定m個訓練樣本S={x^(i),y⁽ⁱ⁾}，通過經驗風險最小化來得到一組權值w，則現在對於整個訓練集待優化目標函式為：

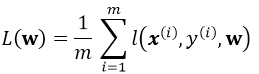
其中為單個訓練樣本（x^(i),y⁽ⁱ⁾）的損失函式，單個樣本的損失表示如下：

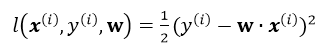
引入L2正則，即在損失函式中引入，那麼最終的損失為：

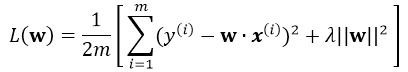
注意單個樣本引入損失為（並不用除以m）：

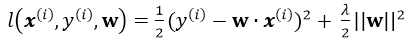
正則化的解釋

這裡的正則化項可以防止過擬合，注意是在整體的損失函式中引入正則項，一般的引入正則化的形式如下：

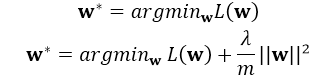
其中L(w)為整體損失，這裡其實有：

這裡的 C即可代表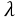，比如以下兩種不同的正則方式：

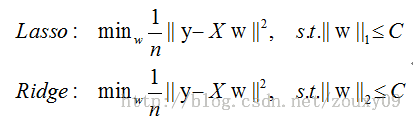
下面給一個二維的示例圖：我們將模型空間限制在w的一個L1-ball 中。為了便於視覺化，我們考慮兩維的情況，在(w1, w2)平面上可以畫出目標函式的等高線，而約束條件則成為平面上半徑為C的一個 norm ball 。等高線與 norm ball 首次相交的地方就是最優解

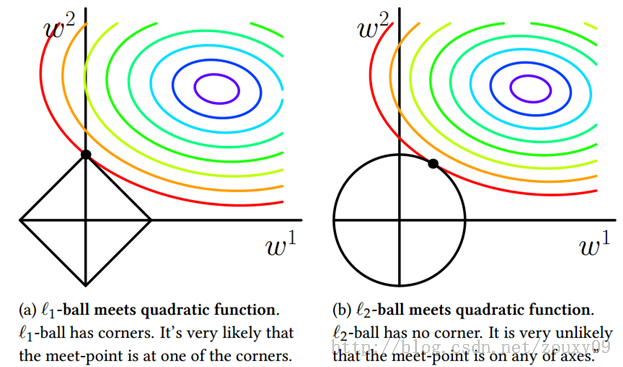
可以看到，L1-ball 與L2-ball 的不同就在於L1在和每個座標軸相交的地方都有“角”出現，而目標函式的測地線除非位置擺得非常好，大部分時候都會在角的地方相交。注意到在角的位置就會產生稀疏性，例如圖中的相交點就有w1=0，而更高維的時候（想象一下三維的L1-ball 是什麼樣的？）除了角點以外，還有很多邊的輪廓也是既有很大的概率成為第一次相交的地方，又會產生稀疏性，相比之下，L2-ball 就沒有這樣的性質，因為沒有角，所以第一次相交的地方出現在具有稀疏性的位置的概率就變得非常小了。

因此，一句話總結就是：L1會趨向於產生少量的特徵，而其他的特徵都是0，而L2會選擇更多的特徵，這些特徵都會接近於0。Lasso在特徵選擇時候非常有用，而Ridge就只是一種規則化而已。

Batch Gradient Descent

有了以上基本的優化公式，就可以用Gradient Descent 來對公式進行求解，假設w的維度為n，首先來看標準的Batch Gradient Descent演算法：

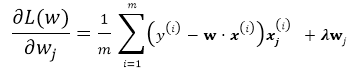
repeat until convergency{

　　for j=1;j<n ; j++:

}

 這裡的批梯度下降演算法是每次迭代都遍歷所有樣本，由所有樣本共同決定最優的方向。

stochastic Gradient Descent

隨機梯度下降就是每次從所有訓練樣例中抽取一個樣本進行更新，這樣每次都不用遍歷所有資料集，迭代速度會很快，但是會增加很多迭代次數，因為每次選取的方向不一定是最優的方向.

repeat until convergency{

　　random choice j from all m training example：

}

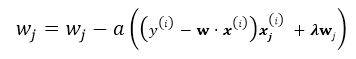
mini-batch Gradient Descent

這是介於以上兩種方法的折中，每次隨機選取大小為b的mini-batch(b<m), b通常取10，或者(2...100),這樣既節省了計算整個批量的時間，同時用mini-batch計算的方向也會更加準確。

repeat until convergency{

　　for j=1;j<n ; j+=b:

}

最後看並行化的SGD：

若最後的v達到收斂條件則結束執行，否則回到第一個for迴圈繼續執行，該方法同樣適用於minibatch gradient descent。