動態規劃之(HMM)和(Viterbi Algorithm)

1. 實際問題

HMM－韋小寶的骰子
• 兩種骰子，開始以2/5的概率出千。
– 正常A：以1/6的概率出現每個點
– 不正常B： 5,6出現概率為3/10,其它為1/10
• 出千的隨機規律

觀測到其一次投擲結果

Y={1,3,4,5,5,6,6,3,2,6}
問題是韋小寶何時出千了？

2. 馬爾可夫模型(HMM)介紹

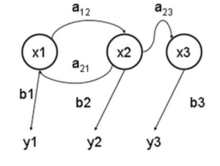
隱馬爾可夫模型（Hidden Markov Model，HMM）作為一種統計分析模型，創立於20世紀70年代。80年代得到了傳播和發展，成為訊號處理的一個重要方向，現已成功地用於語音識別，行為識別，文字識別以及故障診斷等領域。模型如下圖所示：

隱馬爾可夫模型是馬爾可夫鏈的一種，它的狀態不能直接觀察到，但能通過觀測向量序列觀察到，每個觀測向量都是通過某些概率密度分佈表現為各種狀態，每一個觀測向量是由一個具有相應概率密度分佈的狀態序列產生。所以，隱馬爾可夫模型是一個雙重隨機過程—-具有一定狀態數的隱馬爾可夫鏈和顯示隨機函式集。自20世紀80年代以來，HMM被應用於語音識別，取得重大成功。到了90年代，HMM還被引入計算機文字識別和行動通訊核心技術“多使用者的檢測”。HMM在生物資訊科學、故障診斷等領域也開始得到應用。
隱馬爾可夫模型（HMM）可以用五個元素來描述，包括2個狀態集合和3個概率矩陣：

2.1 HMM數學模型表達

(1)隱過程為X

={X1,X2,X3,...,XT}
(2)觀察過程為Y={Y1,Y2,Y3,...,YT}
(3)模型引數{π,A,B}

2.1.1 HMM模型各引數詳細說明

(1). 隱含狀態 S
這些狀態之間滿足馬爾可夫性質，是馬爾可夫模型中實際所隱含的狀態。這些狀態通常無法通過直接觀測而得到。（例如S1、S2、S3等等)
(2). 可觀測狀態Y
在模型中與隱含狀態相關聯，可通過直接觀測而得到。(例如Y1,Y2,Y3,...,YT等等，可觀測狀態的數目不一定要和隱含狀態的數目一致）
(3). 初始狀態概率矩陣π
表示隱含狀態在初始時刻t=1或t=0的概率矩陣，(例如t=1時，P(S1)=p1、P(S2)=P2、P(S3)=p3，則初始狀態概率矩陣 π=[ p1 p2 p3 ].
(4). 隱含狀態轉移概率矩陣 A

。
描述了HMM模型中各個狀態之間的轉移概率。
其中Aij=P(Sj|Si),1≤i,,j≤N.表示在 t 時刻、狀態為 Si的條件下，在t+1時刻狀態是 Sj的概率。
(5). 觀測狀態轉移概率矩陣 B （英文名為Confusion Matrix，直譯為混淆矩陣不太易於從字面理解）。
令N代表隱含狀態數目，M代表可觀測狀態數目，則：
Bij=P(Yi|Sj),1≤i≤M,1≤j≤N.
表示在 t 時刻、隱含狀態是 Sj 條件下，觀察狀態為 Oi 的概率。
總結：一般的，可以用λ=(A,B,π)三元組來簡潔的表示一個隱馬爾可夫模型。隱馬爾可夫模型實際上是標準馬爾可夫模型的擴充套件，添加了可觀測狀態集合和這些狀態與隱含狀態之間的概率關係。

3. Viterbi演算法介紹

維特比演算法是一種動態規劃演算法用於尋找最有可能產生觀測事件序列的-維特比路徑-隱含狀態序列,特別是在馬爾可夫資訊源上下文和隱馬爾可夫模型中。術語“維特比路徑”和“維特比演算法”也被用於尋找觀察結果最有可能解釋相關的動態規劃演算法。例如在統計句法分析中動態規劃演算法可以被用於發現最可能的上下文無關的派生(解析)的字串，有時被稱為“維特比分析”。維特比演算法由安德魯·維特比(Andrew Viterbi)於1967年提出，用於在數字通訊鏈路中解卷積以消除噪音。 此演算法被廣泛應用於CDMA和GSM數字蜂窩網路、撥號調變解調器、衛星、深空通訊和802.11無線網路中解卷積碼。現今也被常常用於語音識別、關鍵字識別、計算語言學和生物資訊學中。例如在語音(語音識別)中，聲音訊號作為觀察到的事件序列,而文字字串,被看作是隱含的產生聲音訊號的原因，因此可對聲音訊號應用維特比演算法尋找最有可能的文字字串。

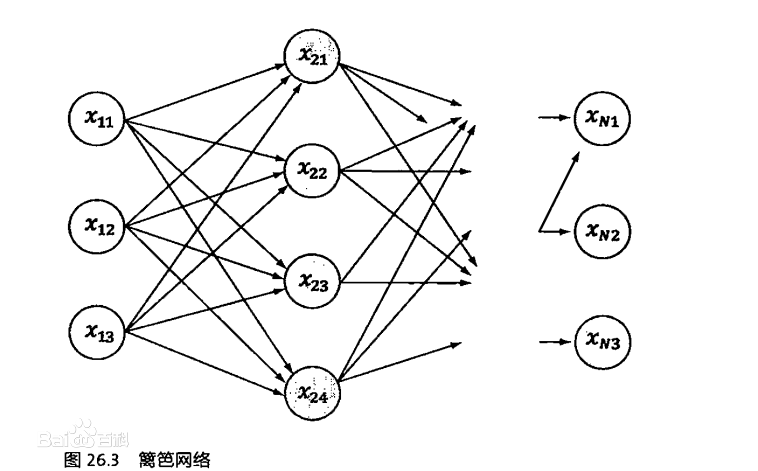
維特比演算法的基礎可以概括成下面三點：
(1)如果概率最大的路徑p(或者說最短路徑)經過某個點，比如途中的X22，那麼這條路徑上的起始點S到X22的這段子路徑Q，一定是S到X22之間的最短路徑。否則，用S到X22的最短路徑R替代Q，便構成一條比P更短的路徑，這顯然是矛盾的。證明了滿足最優性原理。
(2)從S到E的路徑必定經過第i個時刻的某個狀態，假定第i個時刻有k個狀態，那麼如果記錄了從S到底i個狀態的所有k個節點的最短路徑，最終的最短路徑必經過其中一條，這樣，在任意時刻，只要考慮非常有限的最短路即可。
(3)結合以上兩點，假定當我們從狀態i進入狀態i+1時，從S到狀態i上各個節的最短路徑已經找到，並且記錄在這些節點上，那麼在計算從起點S到第i+1狀態的某個節點Xi+!的最短路徑時，只要考慮從S到前一個狀態i所有的k個節點的最短路徑，以及從這個節點到Xi+1，j的距離即可。

3.1 Viterbi演算法虛擬碼描述

現在我們回到問題：
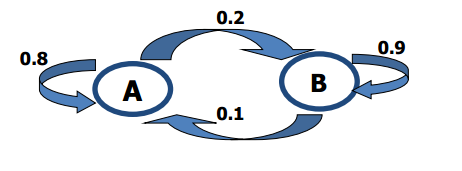
構建模型三個引數如下：

接下來進行用Viterbi演算法求解，實現過程如下：

/********************************************************
Description: Hidden Markov Model(HMM) and Viterbi's decoding Algorithm 
Author:Rosun
Date:2016.10.28
********************************************************/
#include<iostream>
#include<iomanip>
using namespace std;
#define NumState 2  //狀態數量 A B 
#define NumViewValue  6//觀測值種類數 
#define ViewSequnceLength  10//觀測到的序列長度 
void Viterbi_Algorithm(float A[][NumState],float B[][NumViewValue],float Pi[],int Y[]); 
int main(){
    float A[NumState][NumState]={{0.8,0.2},
                                 {0.1,0.9}};//狀態轉移矩陣
    cout<<"輸出轉移矩陣A:"<<endl;
    for(int i=0;i<NumState;i++){
        for(int j=0;j<NumState;j++){
            cout<<setw(4)<<A[i][j]<<" ";
        }
        cout<<endl;
    }
    float B[NumState][NumViewValue]={{1.0/6,1.0/6,1.0/6,1.0/6,1.0/6,1.0/6,},
                                    {1.0/10,1.0/10,1.0/10,1.0/10,3.0/10,3.0/10,}};//B矩陣 
    cout<<"輸出矩陣B:"<<endl;
    for(int i=0;i<NumState;i++){
        for(int j=0;j<NumViewValue;j++){
            cout<<setw(10)<<B[i][j]<<" ";
        }
        cout<<endl;
    }
    float Pi[NumState]={0.6,0.4};//初始各狀態分佈矩陣
    cout<<"輸出初始狀態分佈："<<endl;
    for(int i=0;i<NumState;i++)
        cout<<setw(4)<<Pi[i]<<" ";
    cout<<endl; 
    int Y[ViewSequnceLength]={1,3,4,5,5,6,6,3,2,6};//觀測序列 
    Viterbi_Algorithm(A, B,Pi,Y);
    return 0;
}
void Viterbi_Algorithm(float A[][NumState],float B[][NumViewValue],float Pi[],int Y[]){
    float delta[ViewSequnceLength][NumState];
    delta[0][0]=Pi[0]*B[0][0];
    delta[0][1]=Pi[1]*B[1][0];
    int path[ViewSequnceLength][NumState];
    path[0][0]=0;path[0][1]=0;
    //迭代 
    for(int t=1;t<ViewSequnceLength;t++){
        for(int j=0;j<NumState;j++){
            float tempMax=0.0;
            int flag_i=0;
            for(int i=0;i<NumState;i++){
                if(delta[t-1][i]*A[i][j]>tempMax){
                    tempMax=delta[t-1][i]*A[i][j];
                    flag_i=i;

                }

            }
            delta[t][j]=tempMax*B[j][Y[t]-1];
            path[t][j]=flag_i;  
        }
    } 
    //終止 求出最大概率 
    int X[ViewSequnceLength];
    X[ViewSequnceLength-1]=0;
    float p=delta[ViewSequnceLength-1][0];
    for(int i=1;i<NumState;i++){
        if(delta[ViewSequnceLength-1][i]>p){
                p=delta[ViewSequnceLength-1][i];
                X[ViewSequnceLength-1]=i;

        }   
    }
    cout<<"Max_probablity="<<p<<endl;
    //回溯
    for(int t=ViewSequnceLength-2;t>=0;t--){
        X[t]=path[t+1][X[t+1]];

    } 
    //資訊輸出 
    cout<<endl;
    float result;
    cout<<"各時刻具體情況："<<endl;
    for(int t=0;t<ViewSequnceLength;t++){
        cout<<"時刻t="<<t<<" ";
        for(int j=0;j<NumState;j++){
                cout<<setw(18)<<delta[t][j]<<" ";
            }
            cout<<endl;
    }
    cout<<"輸出隱含過程："<<endl; 
    for(int t=0;t<ViewSequnceLength;t++){
            cout<<setw(4)<<X[t]<<" ";
    }
    char charX[ViewSequnceLength];
    for(int t=0;t<ViewSequnceLength;t++){
        if(X[t]==0)
            charX[t]='A';
        else 
            charX[t]='B';
    }
    cout<<endl;
    for(int t=0;t<ViewSequnceLength;t++){
            cout<<setw(4)<<charX[t]<<" ";
    }
    cout<<endl<<"輸出觀測序列："<<endl;
    for(int t=0;t<ViewSequnceLength;t++){
            cout<<setw(4)<<Y[t]<<" ";
    }

}

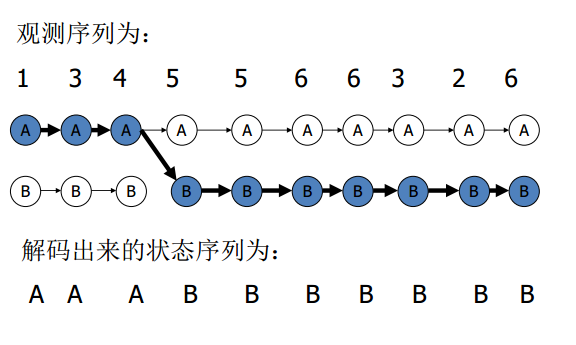
執行結果如下：

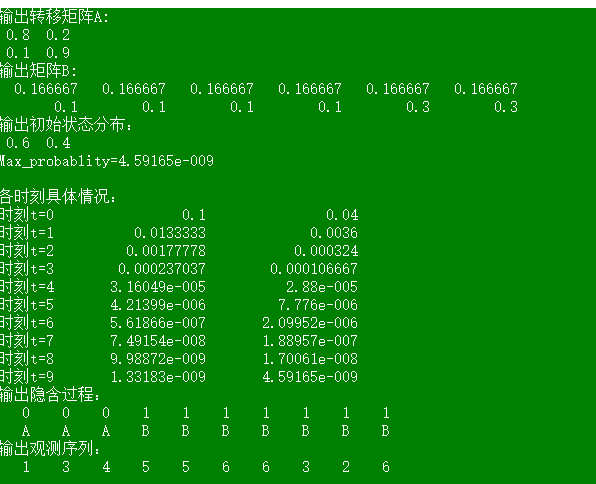
更形象展示結果：

我們可以知道韋小寶在第四次出千啦！好狡猾的！！！