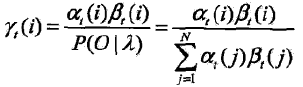隱馬爾可夫模型(HMM)
宣告:
1,本篇為個人對《2012.李航.統計學習方法.pdf》的學習總結,不得用作商用,歡迎轉載,但請註明出處(即:本帖地址)。
2,由於本人在學習初始時有很多數學知識都已忘記,所以為了弄懂其中的內容查閱了很多資料,所以裡面應該會有引用其他帖子的小部分內容,如果原作者看到可以私信我,我會將您的帖子的地址付到下面。
3,如果有內容錯誤或不準確歡迎大家指正。
4,如果能幫到你,那真是太好了。
這裡介紹隱馬爾可夫模型預測的兩種演算法:近似演算法與維特比演算法。
近似演算法
近似演算法的想法是:在每個時刻t選擇在該時刻最有可能出現的狀態it
給定隱馬爾可夫模型λ和觀測序列O,在時刻t處於狀態qi的概率γt(i)是
在每一時刻t最有可能的狀態it*是
從而得到狀態序列I* =(i1*, i2*, ..., iT*)。
近似演算法的有點是計算簡單,其缺點是不能保證預測的狀態序列整體是最有可能的狀態序列,因為預測的狀態序列可能有實際不發生的部分。
事實上,上述方法得到的狀態序列中有可能存在轉移概率為0的相鄰狀態,即,對某些i, j,aij
儘管如此,近似演算法仍然是有用的。
維特比演算法
維特比演算法實際上用動態規劃隱馬爾可夫模型預測問題,即,用動態規劃(dunamic programming)求概率最大路徑(最優路徑)。這時一條路徑對應著一個狀態序列。
根據動態規劃原來,最優路徑具有這樣的特徵:如果最優路徑在時刻t通過節點it*,那麼這一路徑中“從節點i1*到終點it*的部分路徑”對於“從節點i1*到終點it*的所有可能的部分路徑”來說必須是最優的。
根據這一原理,我們只需從時刻t=1開始,遞推的計算在時刻t狀態為i的各條部分路徑的最大概率,直至得到時刻t=T時狀態為i的各條路徑的最大概率。時刻t=T的最大概率即為最優路徑的概率P*,最優路徑的終點it
之後,為了找出最優路徑的各個節點,從終結點iT*開始,由後向前逐步求得節點iT-1*,..., i1*,得到最優路徑I* = (i1*, i2*, ..., iT*)。
這就是維特比演算法。
首先匯入兩個變數δ和ψ。定義在時刻t狀態為i的所有單個路徑(i1, i2, ..., it)中概率最大值為:
由定義可得變數δ的遞推公式:
定義在時刻t狀態為i的所有單個路徑(i1,i2, ... , it-1, it)中概率最大的路徑的第t-1個節點為
於是維特比演算法如下。
演算法(維特比演算法):
輸入:模型λ= (A, B,π)和觀測O=(o1,o2, ..., oT);
輸出:最優路徑I* = (i1*,i2*, ..., iT*)。
過程:
例子
考慮盒子和球模型λ=(A, B,π),狀態集合Q={1, 2, 3},觀測集合V={紅, 白},
已知觀測序列O=(紅,白,紅),試求最優狀態序列,即最優路徑I* = (i1*, i2*, i3*)。
解:
如下圖所示(圖中的數字在之後的步驟中會一一推匯出來)
要在所有可能的路徑中選擇一條最優路徑,按照以下步驟出來。
1,初始化
在t=1時,對每個狀態i,i=1, 2, 3,求狀態為i觀測o1為紅的概率,記此概率為δ1(i),則:
δ1(i) = πibi(o1) =πibi(紅), i = 1, 2, 3
代入實際資料
δ1(1) = 0.10,δ1(2) = 0.16,δ1(3) = 0.28
記ψ1(i) = 0,i = 1, 2, 3。
2,在t=n時
在t=2時,對每個狀態i, i =1,2,3,求在t=1時狀態為j觀測為紅並在t=2時狀態為i觀測o2為白的路徑的最大概率,記此最大概率為δ2(i),則:
同時,對每個狀態i, i= 1, 2, 3,記錄概率最大路徑的前一個狀態j:
計算:
同樣,在t=3時
3,求最優路徑的終點
以P*表示最優路徑的概率,則
最優路徑的終點是i3*:
4,逆向找i2*,i1*:
在t=2時,i2*= ψ3(i3*) =ψ3(3) = 3
在t=2時,i1*= ψ2(i2*) =ψ2(3) = 3
於是求得最優路徑,即最有狀態序列I* = (i1*, i2*, i3*)= (3, 3, 3)。