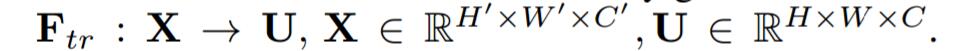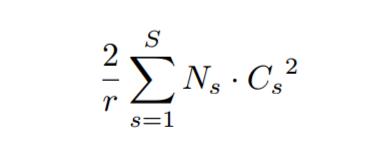SENet（Squeeze-and-Excitation Networks）網路詳解
一、SENet概述
Squeeze-and-Excitation Networks（簡稱 SENet）是 Momenta 胡杰團隊（WMW）提出的新的網路結構，利用SENet，一舉取得最後一屆 ImageNet 2017 競賽 Image Classification 任務的冠軍，在ImageNet資料集上將top-5 error降低到2.251%，原先的最好成績是2.991%。
作者在文中將SENet block插入到現有的多種分類網路中，都取得了不錯的效果。作者的動機是希望顯式地建模特徵通道之間的相互依賴關係。另外，作者並未引入新的空間維度來進行特徵通道間的融合，而是採用了一種全新的「特徵重標定」策略。具體來說，就是通過學習的方式來自動獲取到每個特徵通道的重要程度，然後依照這個重要程度去提升有用的特徵並抑制對當前任務用處不大的特徵。
通俗的來說SENet的核心思想在於通過網路根據loss去學習特徵權重，使得有效的feature map權重大，無效或效果小的feature map權重小的方式訓練模型達到更好的結果。SE block嵌在原有的一些分類網路中不可避免地增加了一些引數和計算量，但是在效果面前還是可以接受的 。Sequeeze-and-Excitation(SE) block並不是一個完整的網路結構，而是一個子結構，可以嵌到其他分類或檢測模型中。
二、SENet 結構組成詳解
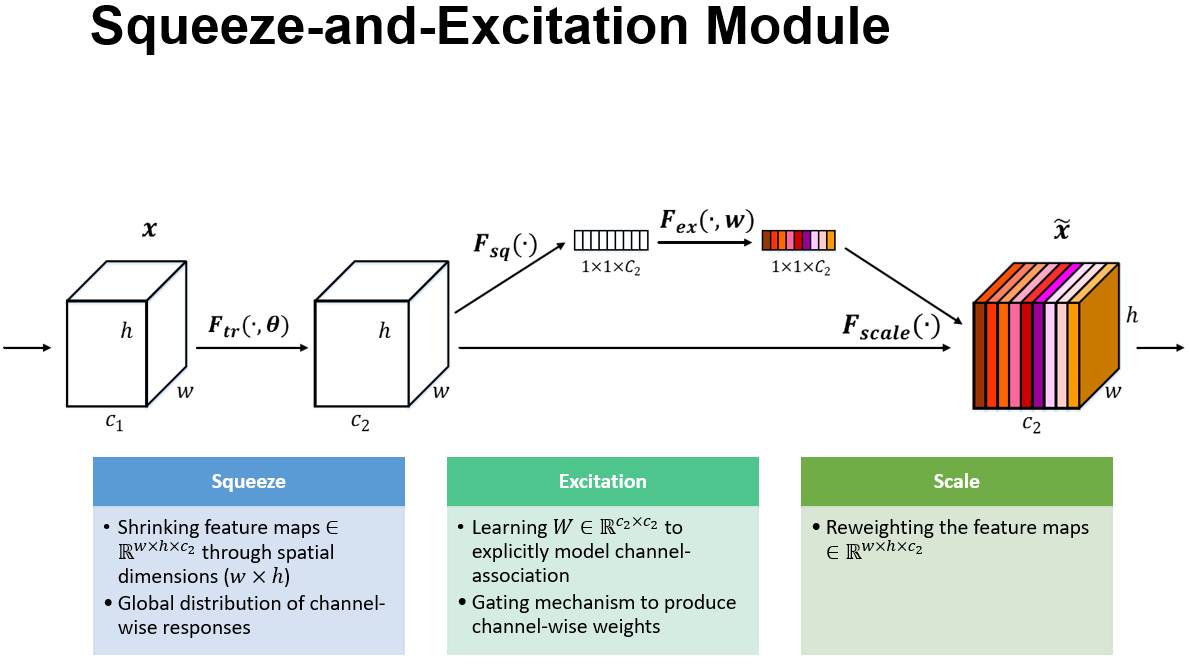
上述結構中，Squeeze 和 Excitation 是兩個非常關鍵的操作，下面進行詳細說明。
上圖是SE 模組的示意圖。給定一個輸入 x，其特徵通道數為 c_1，通過一系列卷積等一般變換後得到一個特徵通道數為 c_2 的特徵。與傳統的 CNN 不一樣的是，接下來通過三個操作來重標定前面得到的特徵。
首先是 Squeeze 操作，順著空間維度來進行特徵壓縮，將每個二維的特徵通道變成一個實數，這個實數某種程度上具有全域性的感受野，並且輸出的維度和輸入的特徵通道數相匹配。它表徵著在特徵通道上響應的全域性分佈，而且使得靠近輸入的層也可以獲得全域性的感受野，這一點在很多工中都是非常有用的。
其次是 Excitation 操作，它是一個類似於迴圈神經網路中門的機制。通過引數 w 來為每個特徵通道生成權重，其中引數 w 被學習用來顯式地建模特徵通道間的相關性。
最後是一個 Reweight 的操作，將 Excitation 的輸出的權重看做是進過特徵選擇後的每個特徵通道的重要性，然後通過乘法逐通道加權到先前的特徵上，完成在通道維度上的對原始特徵的重標定。
首先Ftr這一步是轉換操作（嚴格講並不屬於SENet，而是屬於原網路，可以看後面SENet和Inception及ResNet網路的結合），在文中就是一個標準的卷積操作而已，輸入輸出的定義如下表示。
那麼這個Ftr的公式就是下面的公式1（卷積操作，vc表示第c個卷積核，xs表示第s個輸入）。
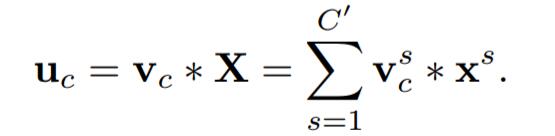Ftr得到的U就是Figure1中的左邊第二個三維矩陣，也叫tensor，或者叫C個大小為H*W的feature map。而uc表示U中第c個二維矩陣，下標c表示channel。接下來就是Squeeze操作，公式非常簡單，就是一個global average pooling: 
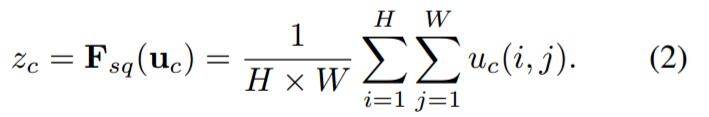因此公式2就將H*W*C的輸入轉換成1*1*C的輸出，對應Figure1中的Fsq操作。為什麼會有這一步呢？這一步的結果相當於表明該層C個feature map的數值分佈情況，或者叫全域性資訊。再接下來就是Excitation操作，如公式3。直接看最後一個等號，前面squeeze得到的結果是z，這裡先用W1乘以z，就是一個全連線層操作，W1的維度是C/r * C，這個r是一個縮放參數，在文中取的是16，這個引數的目的是為了減少channel個數從而降低計算量。又因為z的維度是1*1*C，所以W1z的結果就是1*1*C/r；然後再經過一個ReLU層，輸出的維度不變；然後再和W2相乘，和W2相乘也是一個全連線層的過程，W2的維度是C*C/r，因此輸出的維度就是1*1*C；最後再經過sigmoid函式，得到s。 
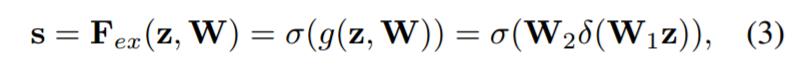也就是說最後得到的這個s的維度是1*1*C，C表示channel數目。這個s其實是本文的核心，它是用來刻畫tensor U中C個feature map的權重。而且這個權重是通過前面這些全連線層和非線性層學習得到的，因此可以end-to-end訓練。這兩個全連線層的作用就是融合各通道的feature map資訊，因為前面的squeeze都是在某個channel的feature map裡面操作。在得到s之後，就可以對原來的tensor U操作了，就是下面的公式4。也很簡單，就是channel-wise multiplication，什麼意思呢？uc是一個二維矩陣，sc是一個數，也就是權重，因此相當於把uc矩陣中的每個值都乘以sc。對應Figure1中的Fscale。
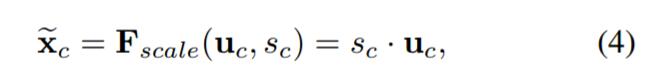
三、SENet 在具體網路中應用
介紹完具體的公式實現，下面介紹下SE block怎麼運用到具體的網路之中。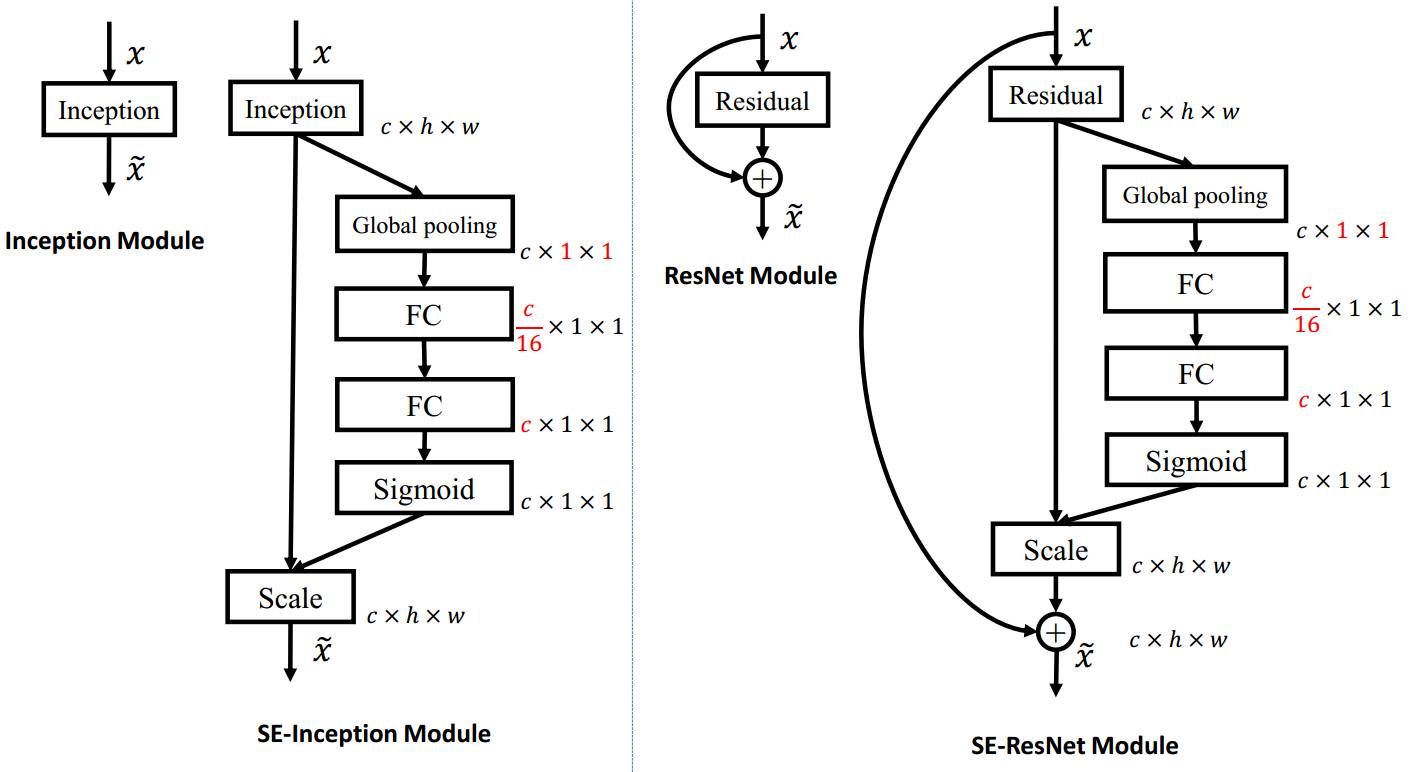
上左圖是將 SE 模組嵌入到 Inception 結構的一個示例。方框旁邊的維度資訊代表該層的輸出。
這裡我們使用 global average pooling 作為 Squeeze 操作。緊接著兩個 Fully Connected 層組成一個 Bottleneck 結構去建模通道間的相關性，並輸出和輸入特徵同樣數目的權重。我們首先將特徵維度降低到輸入的 1/16，然後經過 ReLu 啟用後再通過一個 Fully Connected 層升回到原來的維度。這樣做比直接用一個 Fully Connected 層的好處在於：1）具有更多的非線性，可以更好地擬合通道間複雜的相關性；2）極大地減少了引數量和計算量。然後通過一個 Sigmoid 的門獲得 0~1 之間歸一化的權重，最後通過一個 Scale 的操作來將歸一化後的權重加權到每個通道的特徵上。
除此之外，SE 模組還可以嵌入到含有 skip-connections 的模組中。上右圖是將 SE 嵌入到 ResNet 模組中的一個例子，操作過程基本和 SE-Inception 一樣，只不過是在 Addition 前對分支上 Residual 的特徵進行了特徵重標定。如果對 Addition 後主支上的特徵進行重標定，由於在主幹上存在 0~1 的 scale 操作，在網路較深 BP 優化時就會在靠近輸入層容易出現梯度消散的情況，導致模型難以優化。
目前大多數的主流網路都是基於這兩種類似的單元通過 repeat 方式疊加來構造的。由此可見，SE 模組可以嵌入到現在幾乎所有的網路結構中。通過在原始網路結構的 building block 單元中嵌入 SE 模組，我們可以獲得不同種類的 SENet。如 SE-BN-Inception、SE-ResNet、SE-ReNeXt、SE-Inception-ResNet-v2 等等。
四、SENet 計算量比較
看完結構，再來看添加了SE block後，模型的引數到底增加了多少。其實從前面的介紹可以看出增加的引數主要來自兩個全連線層，兩個全連線層的維度都是C/r * C，那麼這兩個全連線層的引數量就是2*C^2/r。以ResNet為例，假設ResNet一共包含S個stage，每個Stage包含N個重複的residual block，那麼整個添加了SE block的ResNet增加的引數量就是下面的公式：
從上面的介紹中可以發現，SENet 構造非常簡單，而且很容易被部署，不需要引入新的函式或者層。除此之外，它還在模型和計算複雜度上具有良好的特性。拿 ResNet-50 和 SE-ResNet-50 對比舉例來說，SE-ResNet-50 相對於 ResNet-50 有著 10% 模型引數的增長。額外的模型引數都存在於 Bottleneck 設計的兩個 Fully Connected 中，由於 ResNet 結構中最後一個 stage 的特徵通道數目為 2048，導致模型引數有著較大的增長，實驗發現移除掉最後一個 stage 中 3 個 build block 上的 SE 設定，可以將 10% 引數量的增長減少到 2%。此時模型的精度幾乎無損失。
參考：
http://www.sohu.com/a/161633191_465975
https://www.zhihu.com/question/63460684
https://blog.csdn.net/wangkun1340378/article/details/79092001
https://blog.csdn.net/xjz18298268521/article/details/79078551